宋修朝李建全杨亚莉

(1-空军工程大学理学院，西安 710051;2-陕西师范大学数学与信息科学学院，西安 710062)

1 引言

由Kermack和Mckendrick在1927年提出的仓室模型[1]是迄今为止研究传染病动力学的最基本的模型.目前，大多数模型仍假设发生率为双线性型的或标准型的[1-3].鉴于很多传染病的传播机制并没有完全为人所知，所以近年来具有非线性发生率的传染病模型越来越受到重视[4-10]，其中文献[4–7]考虑了非线性发生率为(q和p是正数)的传染病模型，文献[8–10]考虑了非线性发生率为g(I)S的传染病模型.Korobeinikov和Maini[11]研究了非线性发生率为f(S,I,N)的传染病模型，函数f(S,I,N)满足如下条件：

1)

2)对于所有的S,I＞0;

3)对所有的S,I＞0.

该文在一定条件下，证明了模型的全局稳定性.

文献[9]考虑了非线性发生率为g(I)S的时滞的SEIR传染病模型，其中β表示一个染病者的传染能力，1/(1+εI)表示当染病者I数目增加时其对发生率的影响.文献[10]考虑了非线性发生率也为g(I)S的SIRS传染病模型，其中(H是正数).显然，g(I)都满足

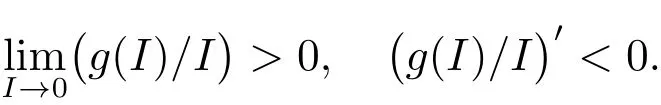
所以，我们将考虑一类具有形式为f(S)g(I)的非线性发生率的SEIR传染病模型，其中函数f(S)和g(I)满足如下条件：

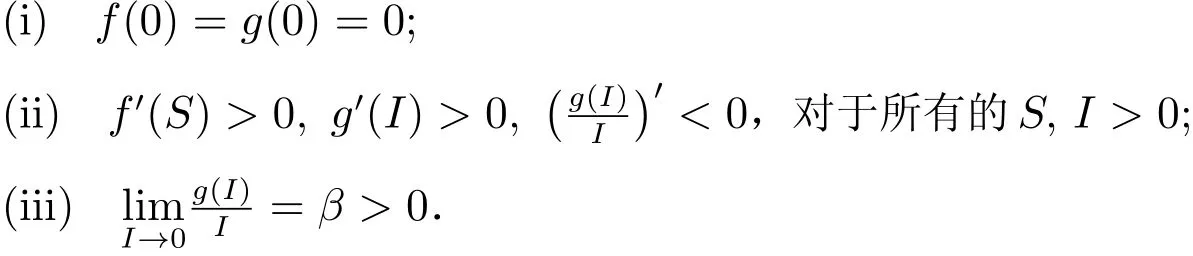
本文考虑的模型是对文献[9]中所考虑模型的发生率的推广，也是对文献[10]中所考虑模型的推广，并且得到了模型全局稳定性的充要条件.在文献[12]中，作者提出了证明具有双线性发生率的传染病模型的全局稳定性的一种代数方法.我们将利用此代数方法证明本文的主要结论.

2 模型及平衡点的存在性

考虑如下传染病模型

在模型(1)中，总人口分为四个仓室：易感者S(t)、潜伏者E(t)、传染者I(t)和恢复者R(t).µA是总人口的常数输入；µ是自然死亡率；q是潜伏者向传染者的转换率；γ是传染者的恢复率；α是因病死亡率.函数f(S)和g(I)满足条件(i),(ii)和(iii).

模型(1)中前三个方程与R无关，因此，考虑如下子系统

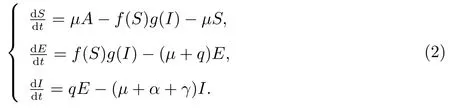
由于

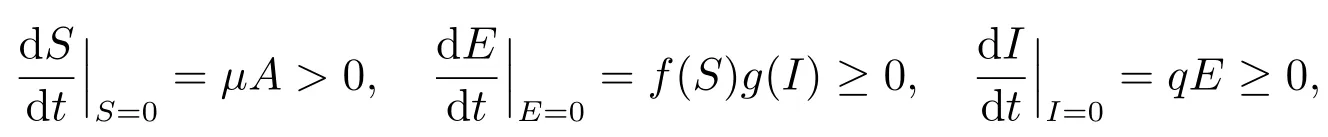
所以系统(2)的初值在R3+中的解的非负性得到了保证.将系统(2)的三个方程相加可得

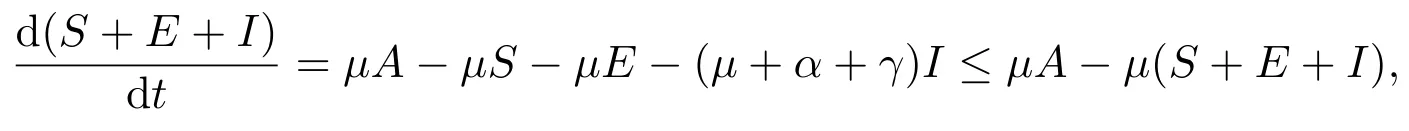
则

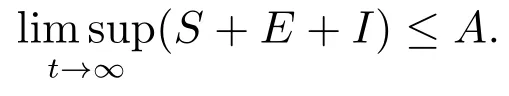
因此，集合是系统(2)的一个正不变集.

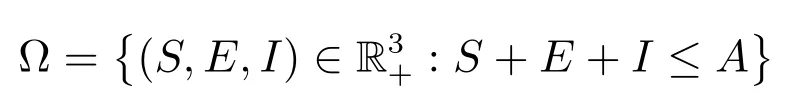
显然系统(2)总存在一个无病平衡点P0(A,0,0).利用再生矩阵[13]可求得系统(2)的基本再生数

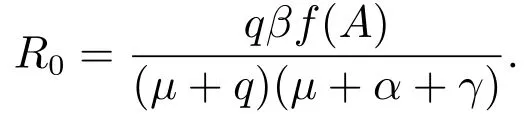
系统(2)的地方病平衡点由方程组

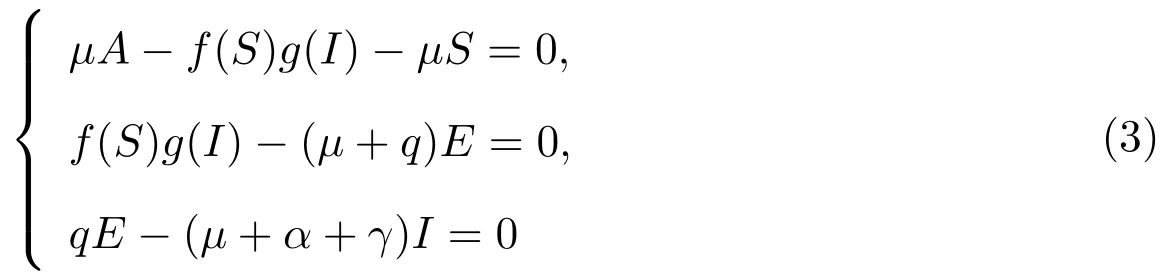
确定.由(3)的最后一个方程可得

将(3)的前两个方程相加得

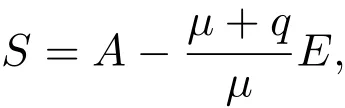
所以

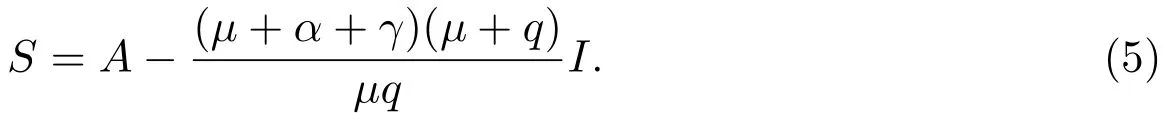
为了保证S＞0，只需

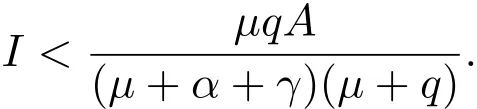
当I/=0时，由(3)的第二个方程和(4)可知

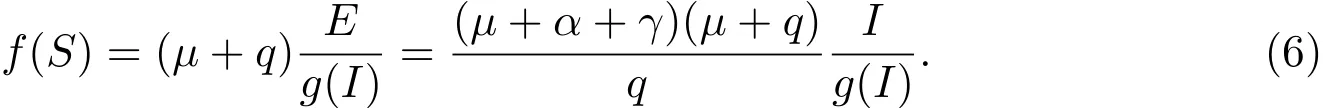
将(5)代入(6)，得

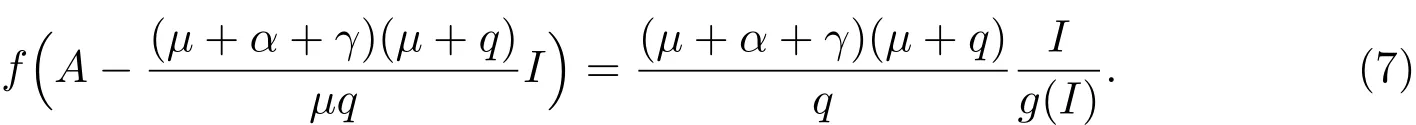
令

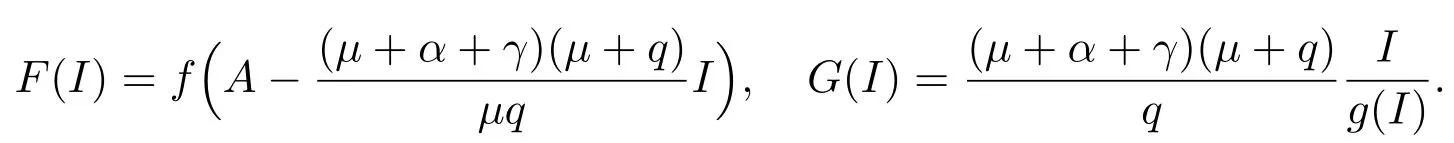
因为f′(S)＞0，所以当

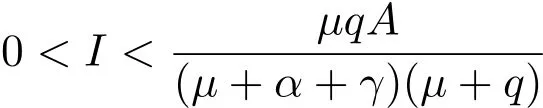
时，函数F(I)是递减的，并且

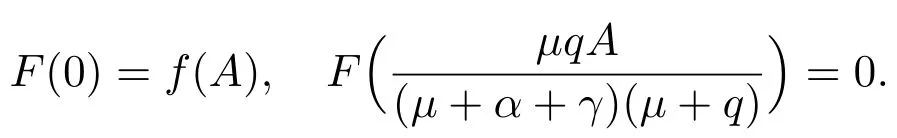
由条件(ii)和(iii)可知：函数G(I)是递增的，并且

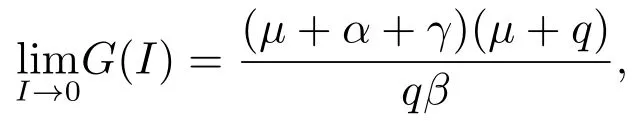
所以当R0＞1，即

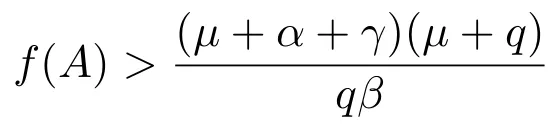
时，方程(7)存在唯一的正根I∗，且

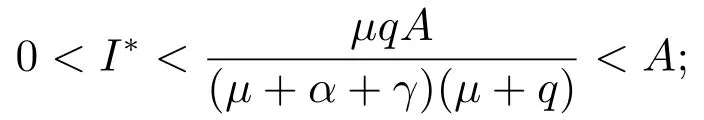
当R0≤1时，方程(7)不存在正根.此时，系统(2)不存在地方病平衡点.所以我们有如下结论：

定理1系统(2)总存在一个无病平衡点当除了外，系统(2)还存在唯一的一个地方病平衡点其中

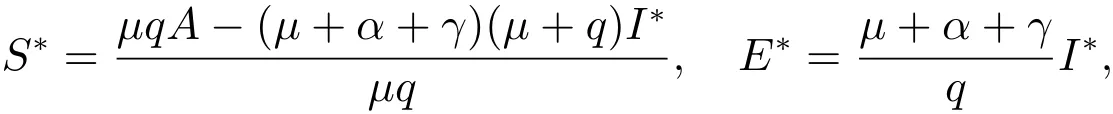
I∗是方程(7)在区间内的正根.

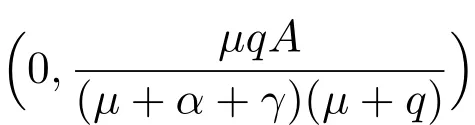
3 平衡点的全局稳定性

在本节中，我们将证明系统(2)的平衡点的全局稳定性.第一个结论是：

定理2当R0≤1时，系统(2)的无病平衡点P0(A,0,0)是全局稳定的；当R0＞1时，P0是不稳定的.

证明 构造如下Lyapunov函数

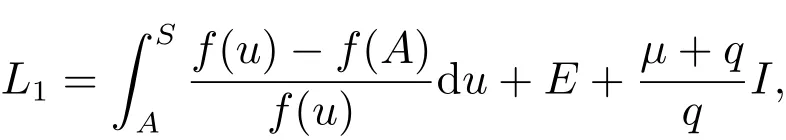
计算L1沿系统(2)解的全导数得

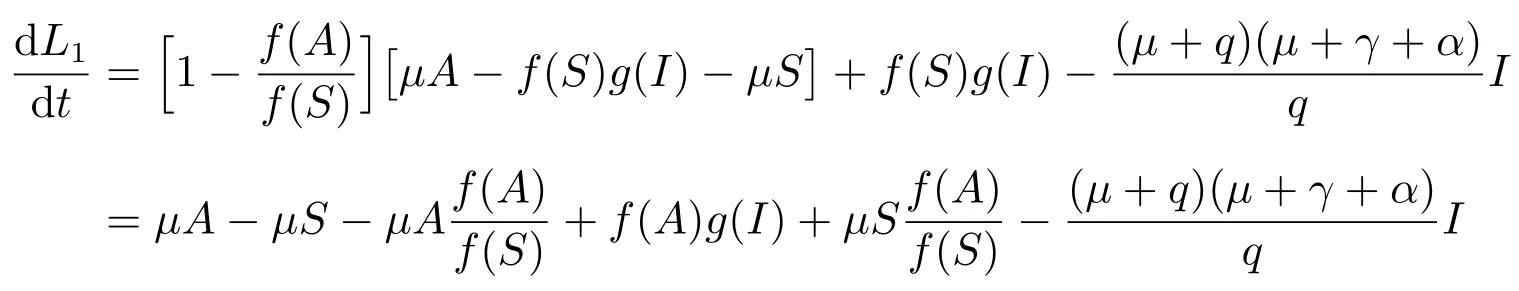
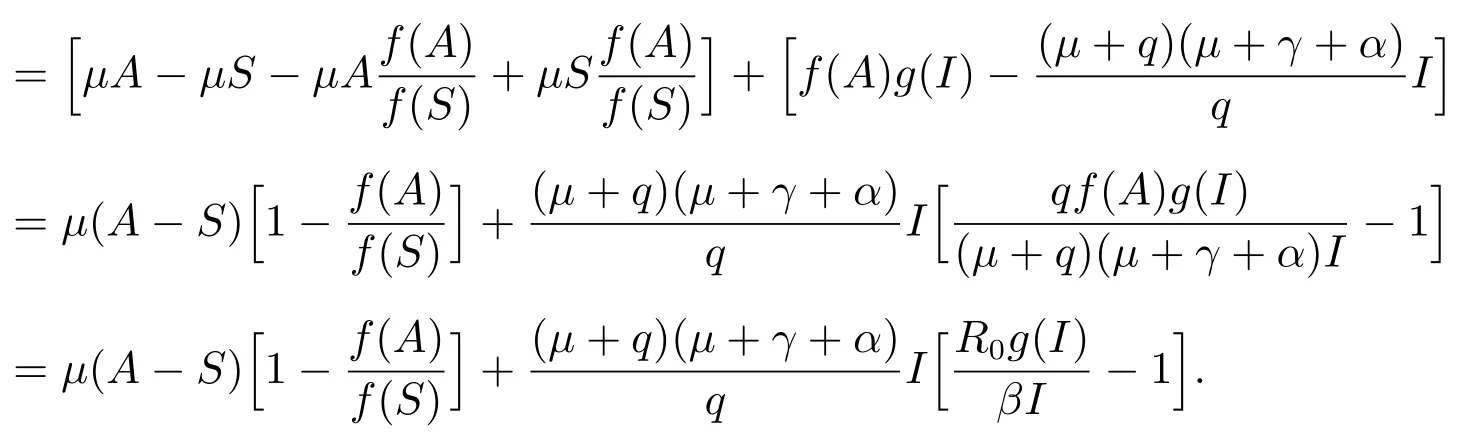
由条件(ii)和(iii)知

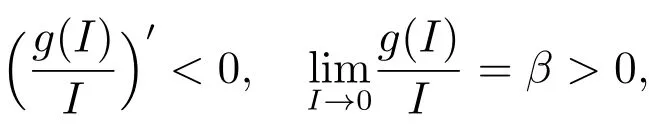
所以

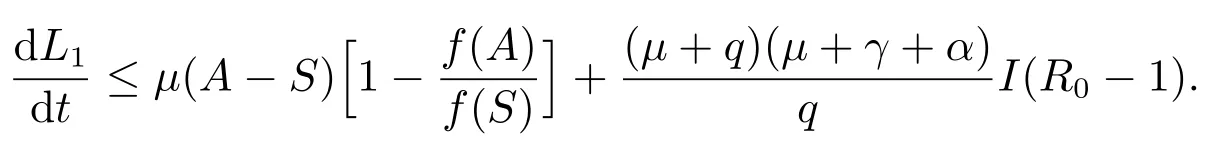
因为对于任意的S＞0，都有所以当S＞0时，

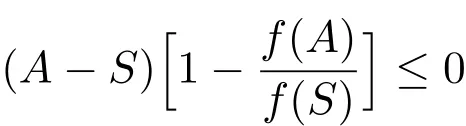
成立.故当时，又因为

所以系统(2)在集合上的最大不变集是单点集

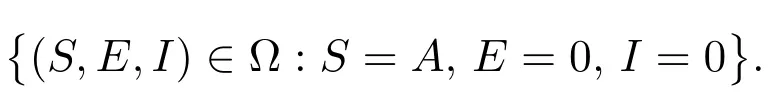
因此，由LaSalle不变性原理[14]可知：当R0≤1时，无病平衡点P0(A,0,0)在集合Ω上是全局稳定的.

系统(2)在P0处的雅可比矩阵为

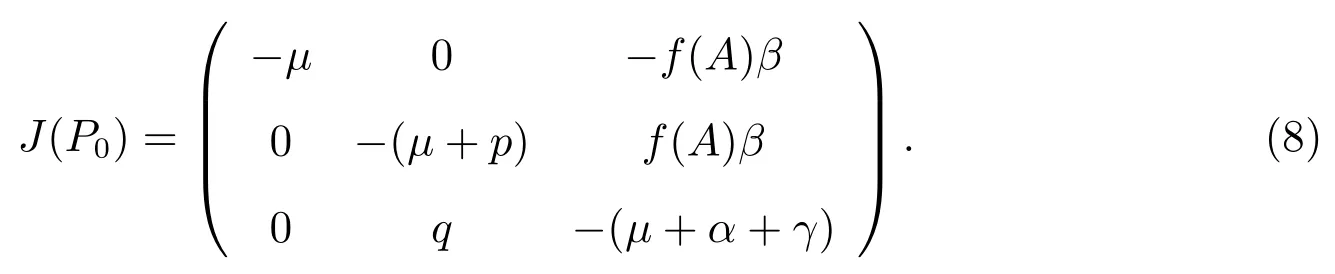
显然，−µ是矩阵J(P0)的一个负特征根，它的另外两个特征根分别是如下矩阵的特征根

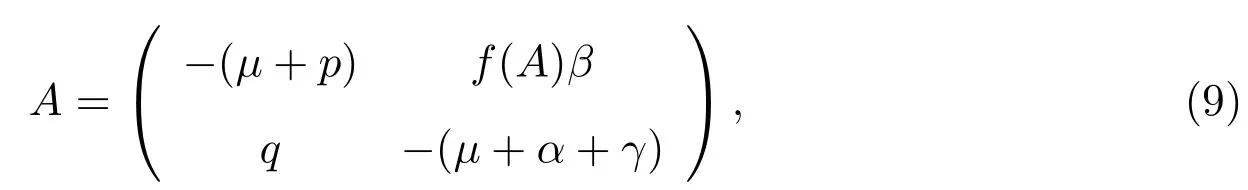
而trA＜0.当R0＞1时，detA＜0，所以矩阵A存在一个正特征值，故当R0＞1时，P0是不稳定的.

本节的第二个结论是：

定理3当R0＞1时，系统(2)唯一的地方病平衡点在Ω的内部是全局稳定的.

证明 构造如下Lyapunov函数

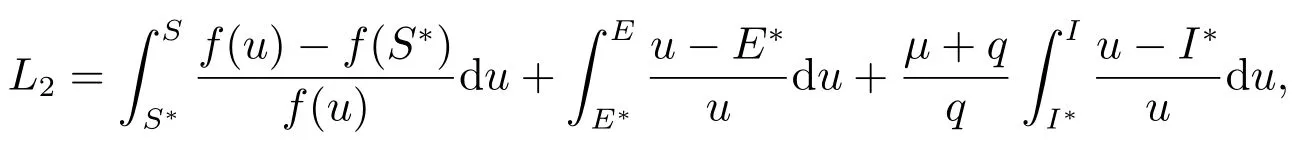
计算L2沿系统(2)解的全导数得

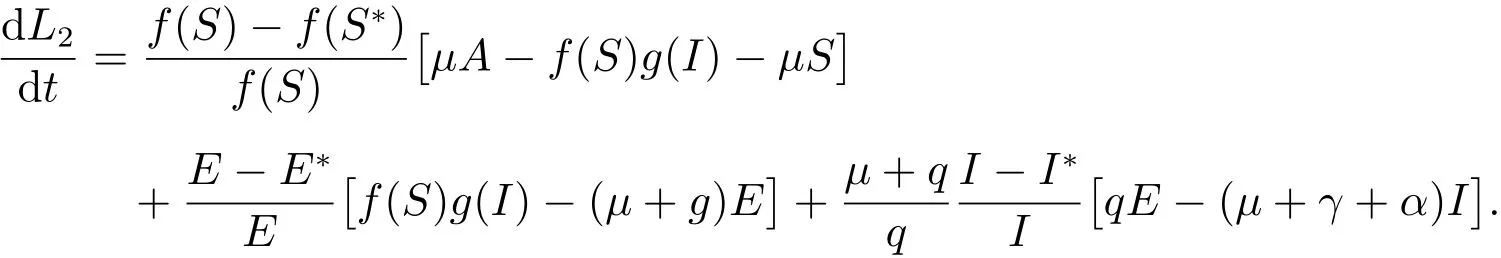
利用(3)可得到

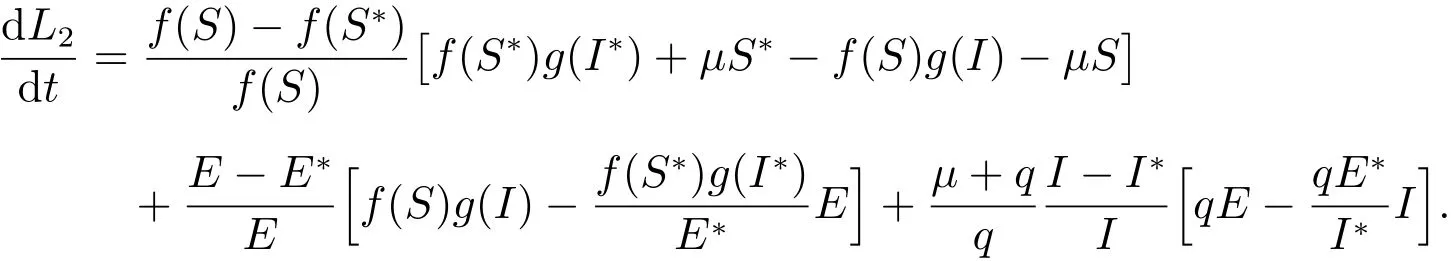
为了书写简单，记

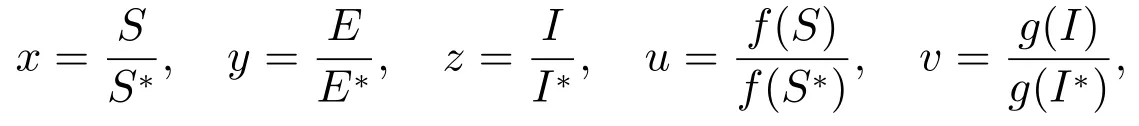
则

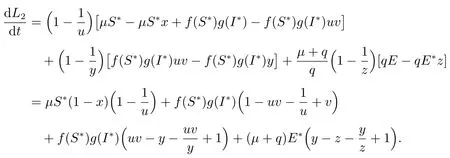
再次利用等式可得

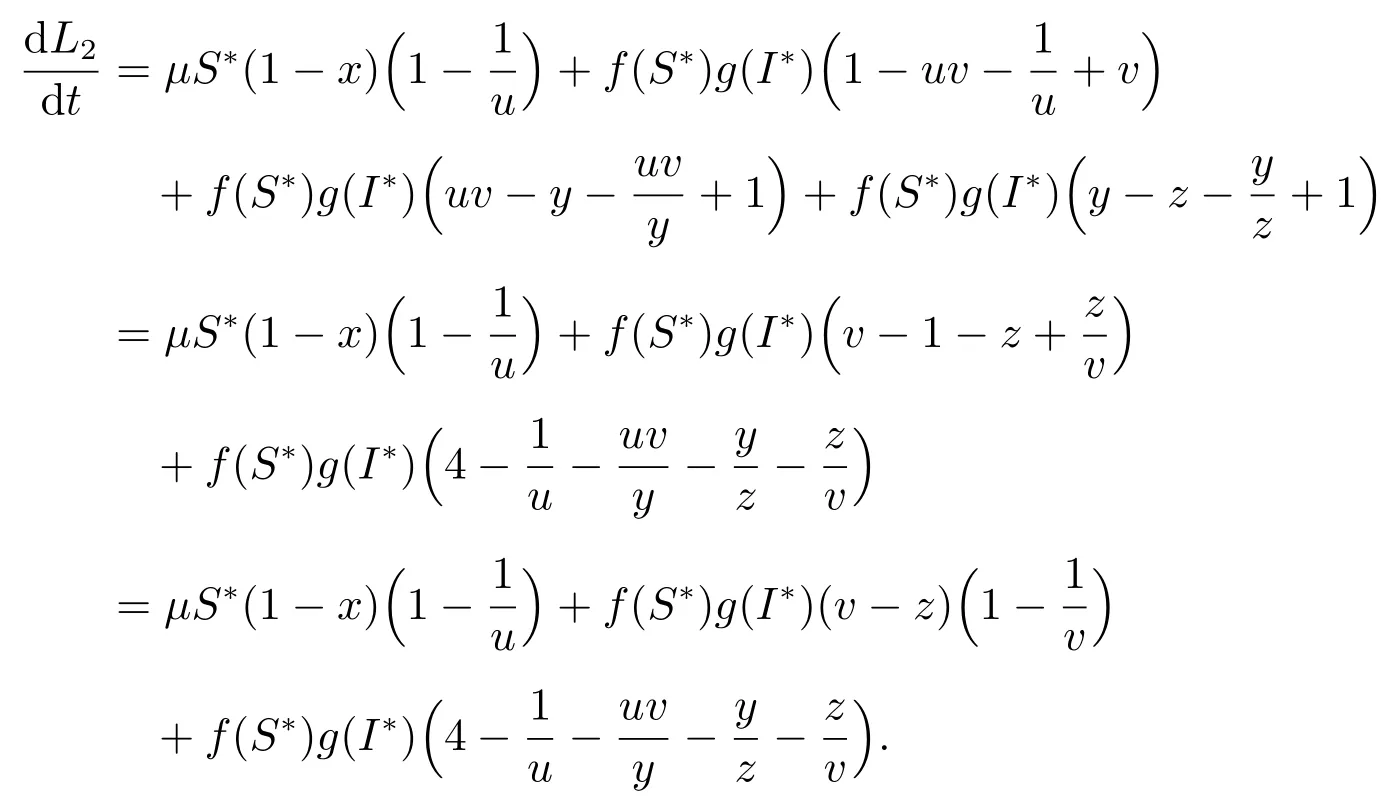
由条件(ii)，可知以下两个式子成立

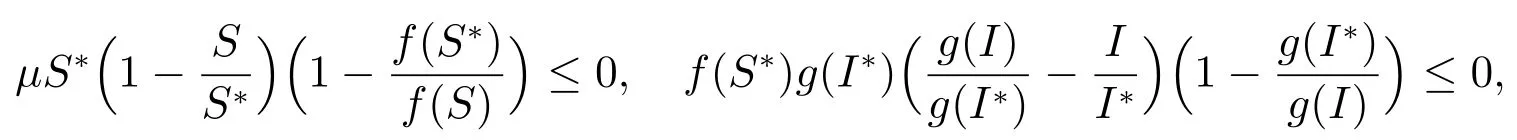
即

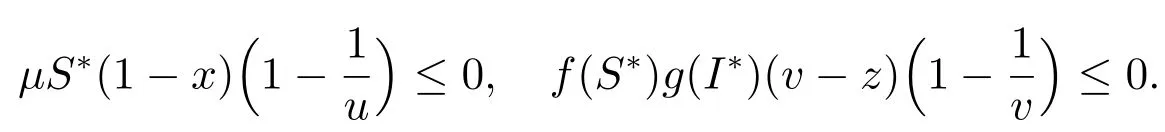
我们知道若干个正数的算术平均数大于或等于它们的几何平均数，所以

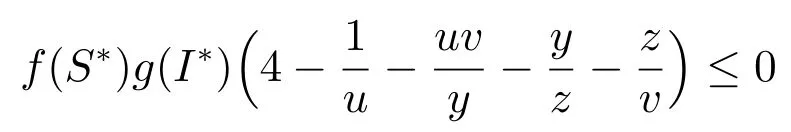
成立.由上可知是负定的，利用李雅普诺夫直接方法[15]可知：当R0＞1时，系统(2)唯一的地方病平衡点在Ω的内部是全局稳定的.

4 讨论

考虑了一类具有非线性发生率的SEIR传染病模型.利用再生矩阵的方法得到了基本再生数，直接计算得到了平衡点的存在性.通过构造恰当的Lyapunov函数，理论上证明了当R0≤1时，无病平衡点是全局稳定的；当R0＞1时，地方病平衡点是全局稳定的.

为了更直观的描述系统(2)的平衡点的稳定性，应用Matlab软件对系统(2)进行数值模拟.不妨取

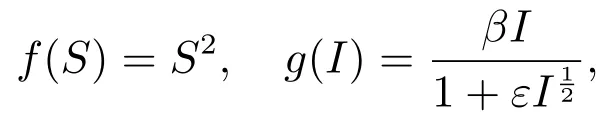
易证f(S),g(I)满足条件(i),(ii)和(iii)，进一步，选取各参数分别为

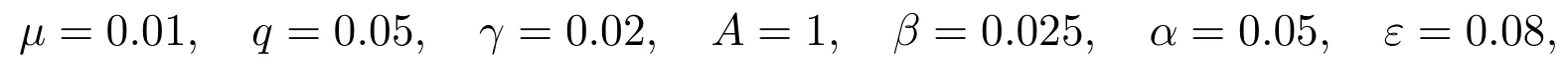
则R0=0.26＜1，此时以三组初值分别为(0.6,0.4,0.3),(0.4,0.5,0.1)和进行数值模拟，如图1(a).可见当时，三条轨线都趋于同时我们也对应给出了传染者I(t)的变化曲线，如图1(b).此时传染者即疾病最终灭亡.当β值取为0.2，其他参数值和初值不变，则相应的基本再生数再进行数值模拟，如图2(a).在这种情形下当时，三条轨线都趋于地方病平衡点.同样，我们也对应给出了传染者I(t)的变化曲线，如图2(b).此时传染者，即形成地方病.这与本文所得定性分析结果一致.这里所用的发生率是已有文献中不曾见到的.

本文所考虑的非线性发生率是通过对文献[8–10]中的发生率的归纳、总结、推广而得到的，具有较好的一般性.我们采用了文献[12]提出的代数方法成功证明了地方病平衡点的全局稳定性，所以说本文将文献[12]提出的证明具有双线性发生率的传染病模型全局稳定性的代数方法推广到了更一般地具有非线性发生率的传染病模型中.

此外，在文献[16]中，作者假设，显然，此时条件不再成立.受此启发，我们将在以后的工作中考虑在没有条件下，系统(2)的全局稳定性.

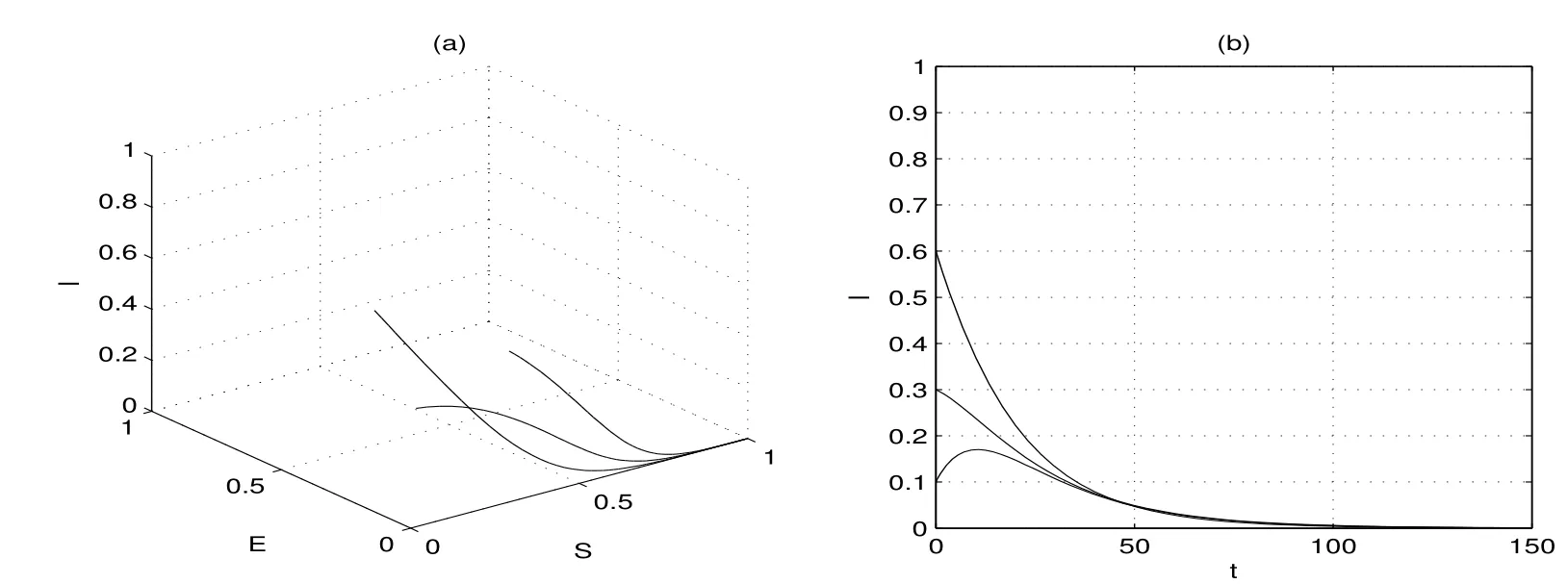
图1:R0＜1时无病平衡点的全局稳定性

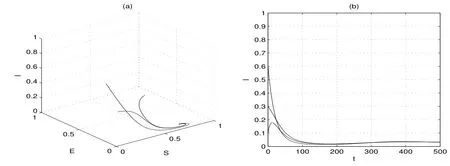
图2:R0＞1时地方病平衡点的全局稳定性

参考文献：

[1]Kermack W O,Mckendrick A G.Contributions to the mathematical theory of epidemics,Part I[J].Proceeding of Royal Society of London,1927,A(115):700-721

[2]Anderson R M,May R M.Infectious Diseases in Humans:Dynamics and Control[M].Oxford:Oxford University Press,1991

[3]Min L,Su Y,Kuang Y.Mathematical analysis of a basic virus infection model with application to HVB infection[J].Rocky Mountain Journal of Mathematics,2008,38(5):1573-1585

[4]Li M Y,Muldowney J S.Global stability for the SEIR model in epidemiology[J].Mathematical Bioscience,1995,125(2):155-164

[5]Hethcote H W,Lewis M A,van den Driessche P.An epidemiological model with a delay and a nonlinear incidence rate[J].Journal of Mathematical Biology,1989,27(1):49-64

[6]Liu W M,Hethcote H W,Levin S A.Dynamical behaviour of epidemiological models with nonlinear incidence rates[J].Journal of Mathematical Biology,1987,25(4):359-380

[7]Liu W M,Levin S A,Iwasa Y.Influence of nonlinear incidence rates upon the behaviour of SIRS epidemiological models[J].Journal of Mathematical Biology,1986,23(2):187-204

[8]Li M Y,Muldowney J S,van den Driessche P.Global stability of SEIRS models in epidemiology[J].Canadian Applied Math Quarterly,1999,7(4):409-425

[9]Beretta E,Breda D.An SEIR epidemic model with constant latency time and infectious period[J].Mathematical Biosciences and Engineering,2011,8(4):931-952

[10]李建全，王拉娣，杨友社.两类含非线性传染率的传染病模型的定性分析[J].空军工程大学学报，2004,5(1):84-88 Li J Q,Wang L D,Yang Y S.Qualitative analysis of nonlinear incidence rate for two epidemic models[J].Journal of Air Force Engineering University,2004,5(1):84-88

[11]Korobeinkov A,Maini P K.Nonlinear incidence and stability of infectious disease models[J].Mathematical Medicine and Biology,2005,22(2):113-128

[12]Li J Q,Xiao Y N,Zhang F Q,et al.An algebraic approach to proving the global stability of a class of epidemic models[J].Nonlinear Analysis:Real World Applications,2012,13(5):2006-2016

[13]van den Driessche P,Watmough J.Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission[J].Mathematical Biosciences,2002,180(1):29-48

[14]LaSalle J P.The Stability of Dynamical Systems[M].New Jersey:Hamilton Press,1976

[15]Verhulst F.Nonlinear Differential Equations and Dynamical Systems[M].Berlin:Springer-Verlag,1996

[16]Kar T K,Batabyal A.Modeling and analysis of an epidemic model with nonmonotonic incidence rate under treatment[J].Journal of Mathematical Research,2010,2(1):103-115