李路程,许晓阳

(1-西北工业大学应用数学系，西安 710129;2-陕西理工学院数学与计算机科学学院，汉中 723001)

1 引言

采用Brown构形场(Brownian configuration fields,BCF)方法[1,2]模拟粘弹性流体问题时，需要耦合求解宏观尺度的守恒方程和介观分子尺度的构形方程.该方法绕开了采用本构方程封闭求解流场控制方程的难点，因而可以摒弃本构方程建立中潜在的不正确性.同时，该方法从介观分子尺度求解聚合物分子构形，故可以得到聚合物的分子信息.

守恒方程和构形方程耦合求解的常见方法有有限元法(finite element method,FEM)[1,2]和有限体积法(finite volume method,FVM)[3-5].FEM能很好地适应不规则区域，而在对流项的处理及对守恒方程的原始变量法求解方面实施起来比较繁琐.虽然FVM的格式精度不高，但是它具有占用内存少、稳定性强和对流项处理简单的优势；同时该方法求解的原守恒方程在每个控制体上都守恒，且物理意义明确.因此，将FVM与BCF方法相结合，是获得聚合物分子信息的有效途径.目前，基于BCF的有限体积方法(finite volume method based on Brownian configuration fields,FVMBCF)鲜有文献研究.代向艳等[6,7]运用FVMBCF方法模拟了Couette流和Poiseuille流，张僡凤等[8]研究了FVMBCF方法的并行算法，并用之模拟了管道流.文献[6–8]中流动问题的求解区域简单，流动特性单一.因此，本文拟应用FVMBCF方法模拟具有复杂流动特性的平板收缩流动问题，以考证该方法模拟复杂流动问题的可靠性.

2 守恒方程

对于不可压缩的等温粘弹性流动，在忽略体积力的情况下，无量纲形式的流场守恒方程[1]为连续方程

动量方程

其中u表示流体速度，Reynolds数Re表示流体惯性力与粘性力的比值，p表示压力，τp表示聚合物应力，粘度比β表示溶剂粘度与流体总粘度的比值.

粘弹性流动问题的流场控制方程包含守恒方程和封闭的应力本构方程.粘弹性流体本构关系的复杂性和机理的不确定性，增加了本构方程建立的难度，BCF方法恰恰绕开了这个难题.

3 BCF方法

BCF方法通过计算大量聚合物分子的构形，根据其系综平均得到聚合物应力.再将介观尺度获得的应力与宏观尺度的守恒方程结合，从而求解粘弹性流场的控制方程.BCF方法求解得到的构形在空间上光滑，确保计算所得的应力光滑[3]；该方法还可以避免CONNFFESSIT(calculation of non-Newtonian fluid:finite element and stochastic simulation techniques)方法[9]中需要追踪大量粒子轨道的问题.

3.1 分子模型

常用的聚合物分子模型有图1所示的珠-簧(链)模型和珠-杆(链)模型.为了表征聚合物分子的粘弹特性，本文选用有限拉伸非线性弹性(finite extensible nonlinear elastic,FENE)珠-簧模型.

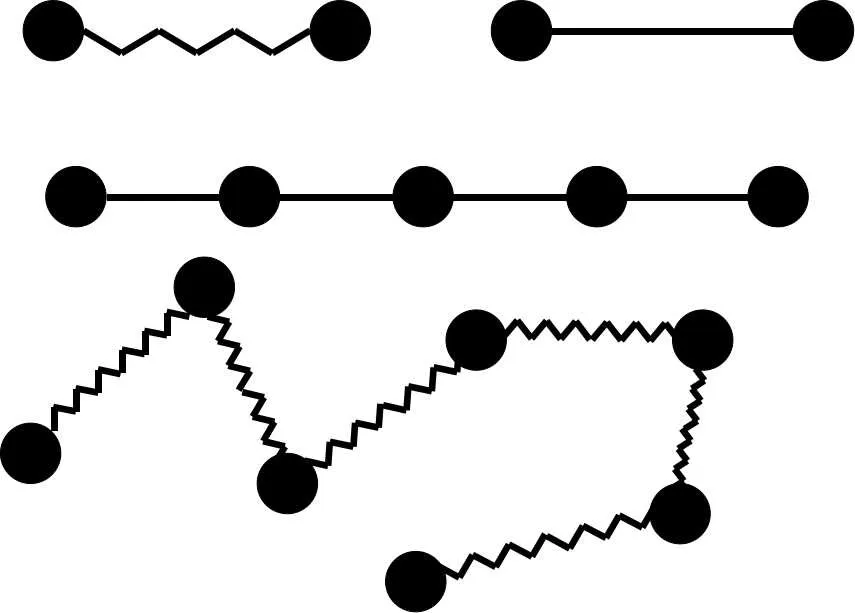
图1:聚合物分子模型示意图

FENE珠-簧模型的弹簧力[1]

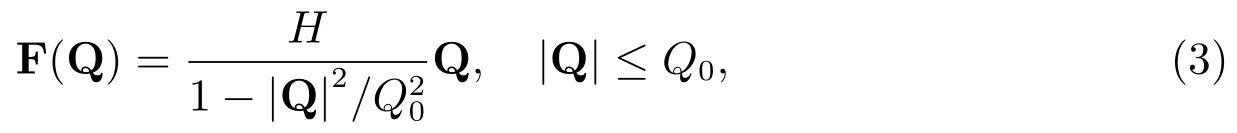
其中Q表示弹簧的构形向量，|Q|是弹簧的长度，Q0是弹簧的最大拉伸量，H是弹簧的弹性系数.

3.2 分子构形演化方程

推导分子构形演化方程，首先需要分析稀溶液中聚合物分子模型中珠子的受力情况.根据Newton第二定律，加速度为零时，珠子i所受的合力公式

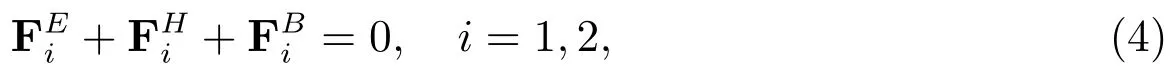
其中和分别代表珠子i所受的弹力、粘滞力和Brown随机力.

弹力

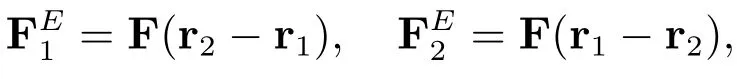
由式(3)给出；粘滞力Brown随机力

计算中常近似为

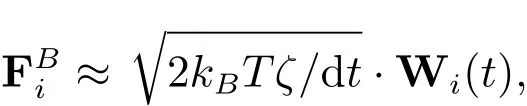
其中ri表示珠子i的位置向量，是i号珠子的速度，表示珠子i处溶剂的速度，ζ为小球与溶剂的摩擦系数，kB为Boltzmann常数，T表示绝对温度，δ表示单位张量，是Markov过程，服从分布

整理方程(4)，得到

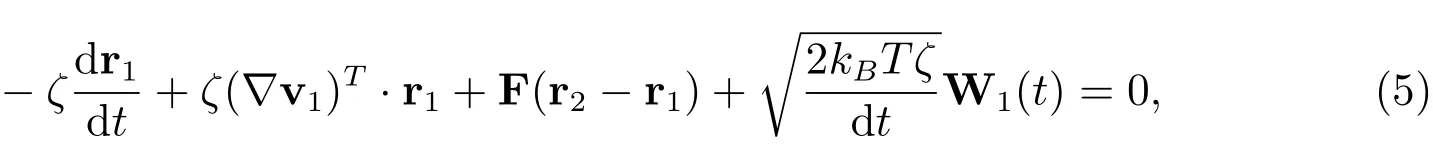
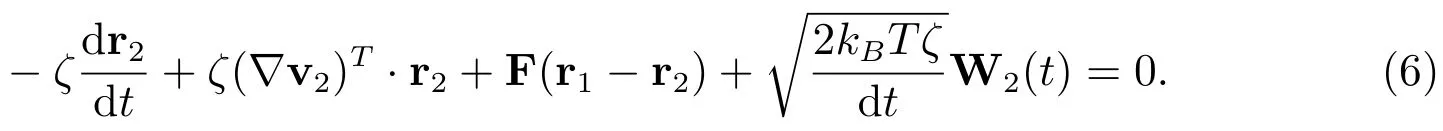
上面两式相减，令Q=r2−r1，根据随体导数公式得到

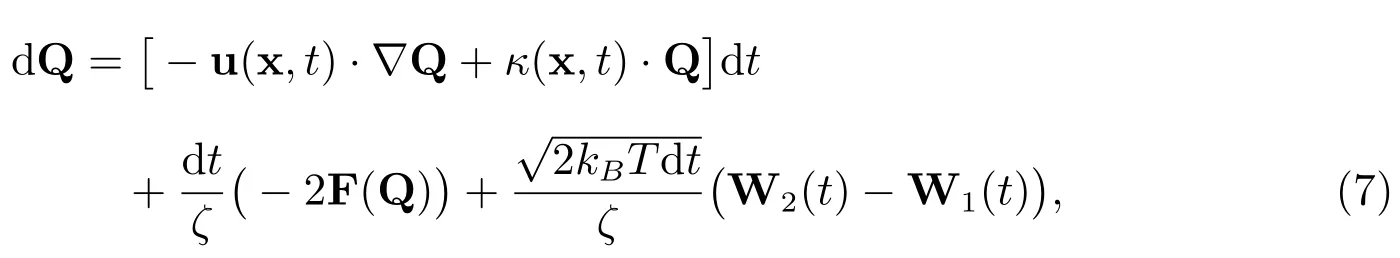
(7)式两端同时除以又有得到

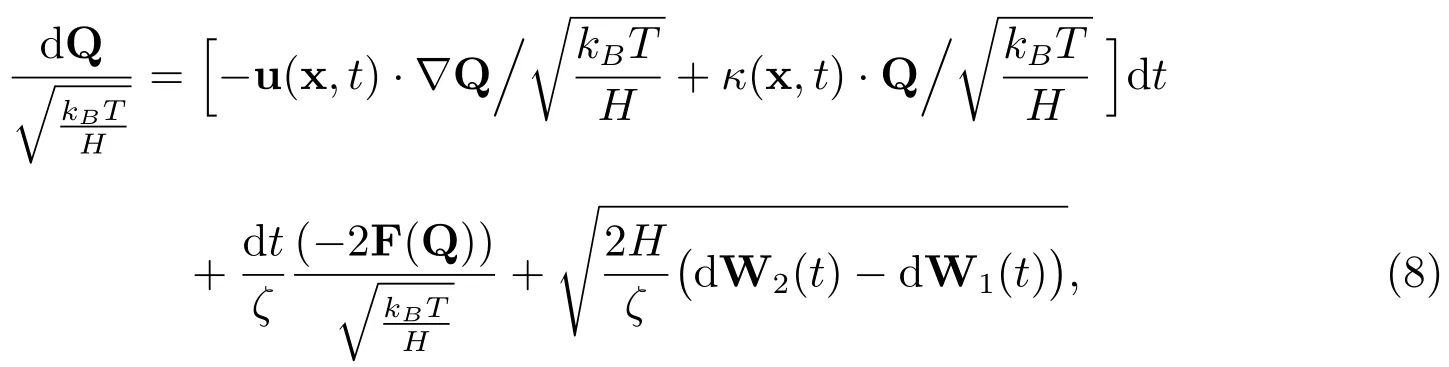
对(8)式进行无量纲处理，得到

其中Weissenberg数，L为流场的特征长度，U为流场的特征速度，Q表示分子模型弹簧的构形向量，κ表示速度梯度的转置，F表示分子模型中弹簧的弹力.

求解方程(9)得到分子构形向量Q后，则由Kramers表达式[3]计算聚合物应力

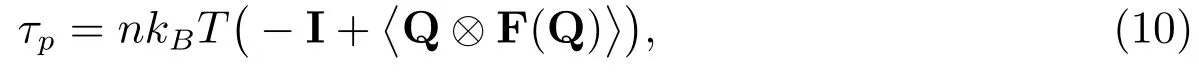
其中nkBT为求解参数，I表示二阶单位矩阵，〈Λ〉表示构形空间上的系综平均，运算符⊗表示两个向量的外积，其表达式为

3.3 施加方差缩减技术的BCF方法

1)设置构形场：在任一计算节点处，设置Nf个编号为j(j=1,K,Nf)的珠-簧模型；在所有节点处编号为j(j=1,K,Nf)的珠-簧模型都具有相同的初始构形，并经历相同的随机过程；

2)引入构形控制变量：初始时刻流体处于静止状态，分子构形服从Gauss随机分布N(0,1)；流动过程中，分子构形的演化由方程(9)来描述；流动趋于稳定时，分子构形最终服从均匀随机分布U(0,1).这表明当前状态应力的变化与平衡状态应力的变化相关，因此，可以选取初始状态服从均匀随机分布，且流动过程中与Q经历相同随机过程的构形作为Q的控制变量[9].针对FENE模型，满足方程

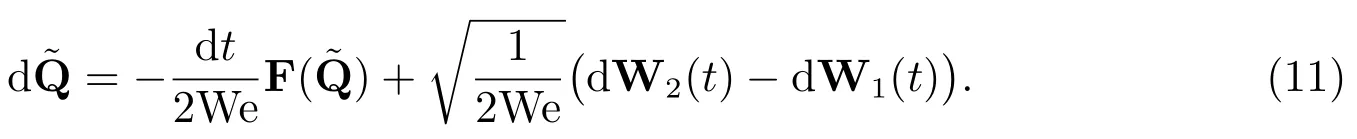
根据式(10)及其恒等变形，有

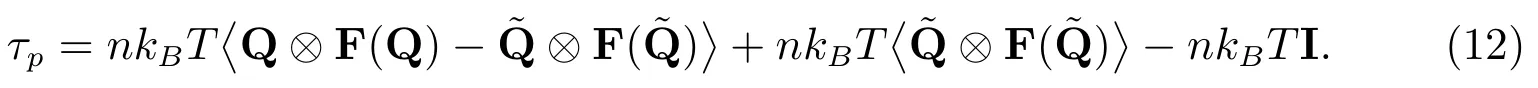
设根据式(12)和外积定义，应力各分量为

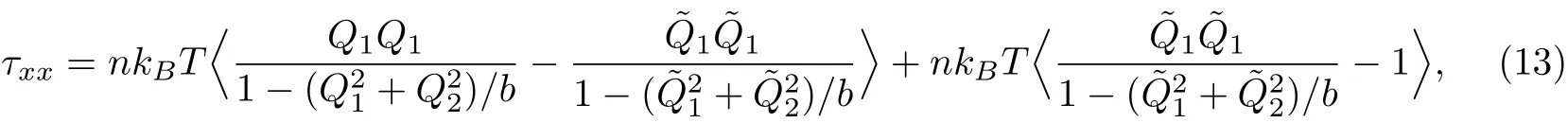
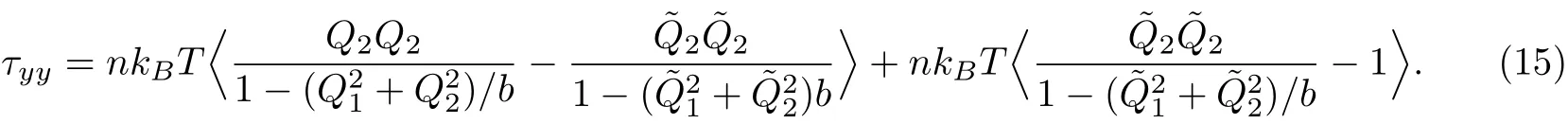
至此，给出了施加方差缩减技术的BCF方法计算聚合物应力各分量的表达式.根据统计学知识，控制变量的引入，不会改变统计量

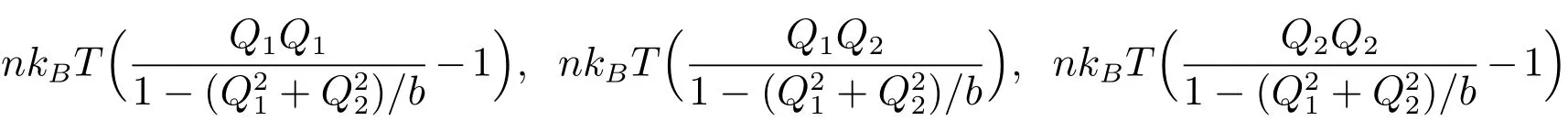
的数学期望；同时，由于控制变量法的统计学性质，它们三个统计量的随机误差将大大地降低.因此，控制变量法的统计学性质使得构形控制变量的引入，能够有效地减少应力的随机误差.

4 数值计算方法

基于Brown构形场方法求解粘弹性流动问题时，首先通过求解聚合物分子的构形方程(9)和控制变量方程(11)，再由式(13)计算聚合物应力，然后将介观尺度求解的应力与宏观尺度的守恒方程(1),(2)结合，从而得到描述粘弹性流动问题的宏观物理量.

4.1 同位网格FVM

本文采用同位网格FVM[5]离散守恒方程(1),(2)，其中对流项的离散采用一阶迎风格式，该格式简单且易于实施.计算中，所有变量置于图2所示的同一套网格.图2中实线交点为计算物理量的存储点，虚线为控制体界面，节点位于控制体的中心.

我撕到最后一页时，听到有人在楼下跟我妈讲话，听我妈那反应就知道来人不是扒锅街的人，她平时的嗓门震得门框都会抖三抖，哪像那会，明明想笑却拼命压着喉咙，像只有痰的老母鸡。

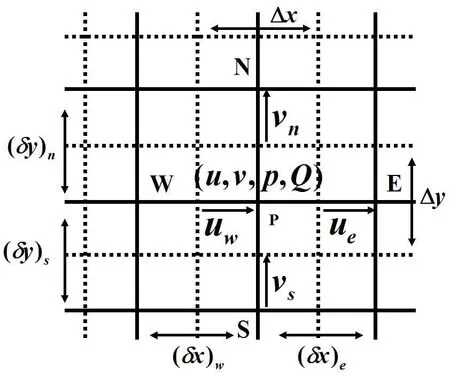
图2:同位网格示意图

将连续方程(1)在图2所示的P控制体上进行积分，其离散格式

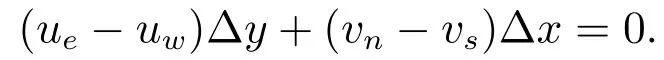
二维动量守恒方程(2)的通量表达形式

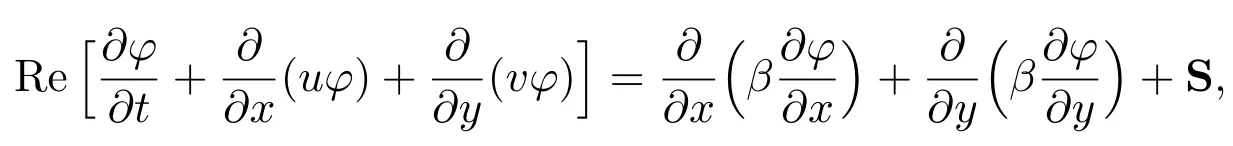
其中

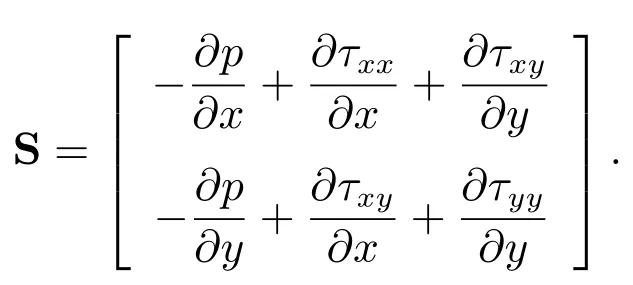
时间项的离散格式精度为一阶；用控制容积积分法对对流-扩散项进行离散

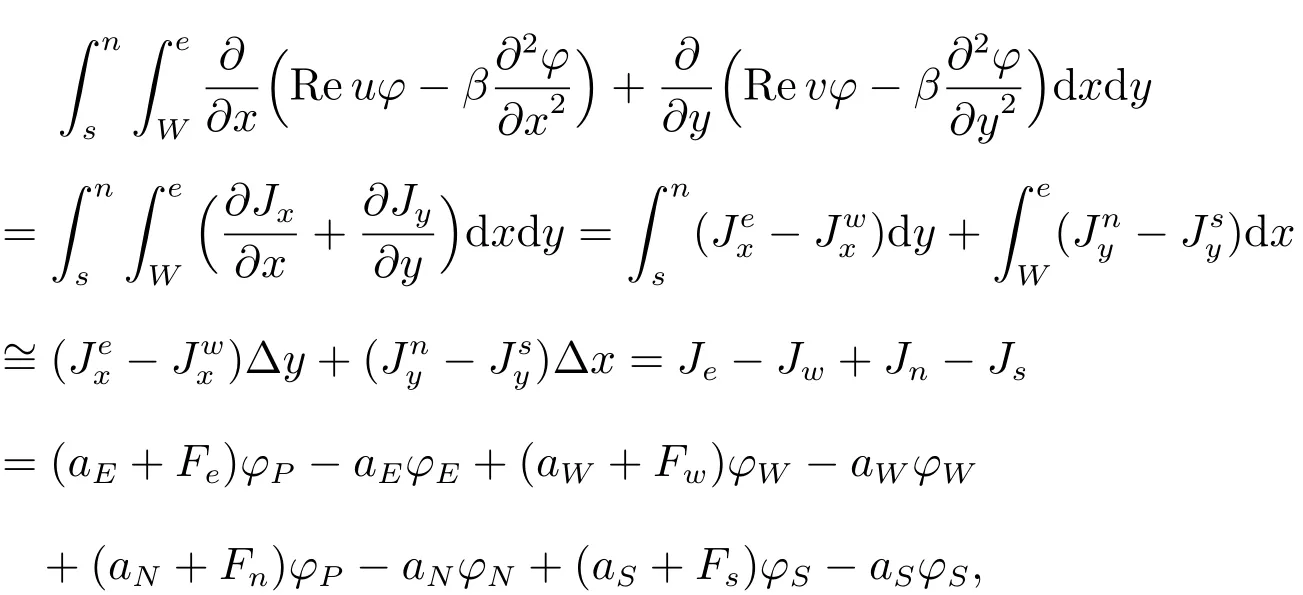
精度为一阶；其中

源项中应力采用显式差分格式离散，压力采用线性插值计算，精度均为一阶；从而有限体积法部分的整体格式精度为一阶.BCF方法是随机方法，难以进行精度分析.设维数d，流动时间步FLAG，收敛判定条件数flag，构形数目Nf，计算点个数M，本文算法的计算量约为

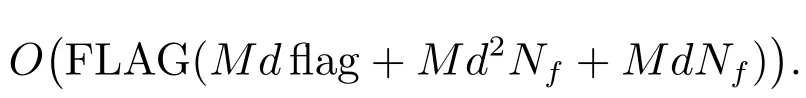
4.2 FVMBCF方法的算法流程

基于并行程序的FVMBCF方法模拟粘弹性流动的具体算法流程如下：

步骤1准备阶段设用P个处理机进行计算，在根进程上给定初始的速度u0，在每个进程上给定初始的分子构形和构形控制变量，初始构形和构形控制变量在空间上分别服从Gauss随机分布和均匀随机分布，它们的数值可由相应的分布函数N(0,1)和U(0,1)独立取样得到；

步骤2计算速度和压力将初始或上一时间步的聚合物应力代入方程(1)和(2)，并用FVM求解，即可得到新的速度和压力；

步骤3计算构形和构形控制变量用新的速度u计算速度梯度κ，并将速度梯度κ广播到每一个进程中去.当已知速度梯度κ及上一时间步的分子构形和构形控制变量时，根据方程(9)和(11)，可计算得到当前时间步的分子构形和构形控制变量

步骤4计算聚合物应力在每个进程上，将步骤3中计算得到的当前时间步的分子构形和构形控制变量代入式(13)，并归约到0进程上求和，计算聚合物应力

步骤5若收敛条件满足，计算结束；否则返回步骤2.

5 数值算例

5.1 Couette流

为了验证施加方差缩减技术的FVMBCF方法的有效性，本文首先基于FENE珠-簧模型，模拟聚合物稀溶液的平板Couette流.

在该流动问题中，聚合物流体被限制在两个距离为L=1.0的平行平板间.当t＜0时，流体和两个平板静止；当t=0，下平板开始以恒定的水平速度u=1.0沿x轴正方向移动，壁面边界满足无滑移边界条件，初始状态为平衡态.为了与文献中的结果进行对比，本文采用文献[11]中的模型参数，即

图3(a)刻画了不同时刻、不同y值处的速度.图3(b)描述了四个不同位置y=0.2,y=0.4,y=0.6,y=0.8处的速度演化.由图3(b)可知，越靠近下平板的位置，速度过冲现象发生的越早.图3(c)描述了图3(b)中的四个位置处的应力演化，应力曲线光滑.模拟结果与文献[11]的结果吻合，从而验证了施加方差缩减技术的FVMBCF方法的有效性.

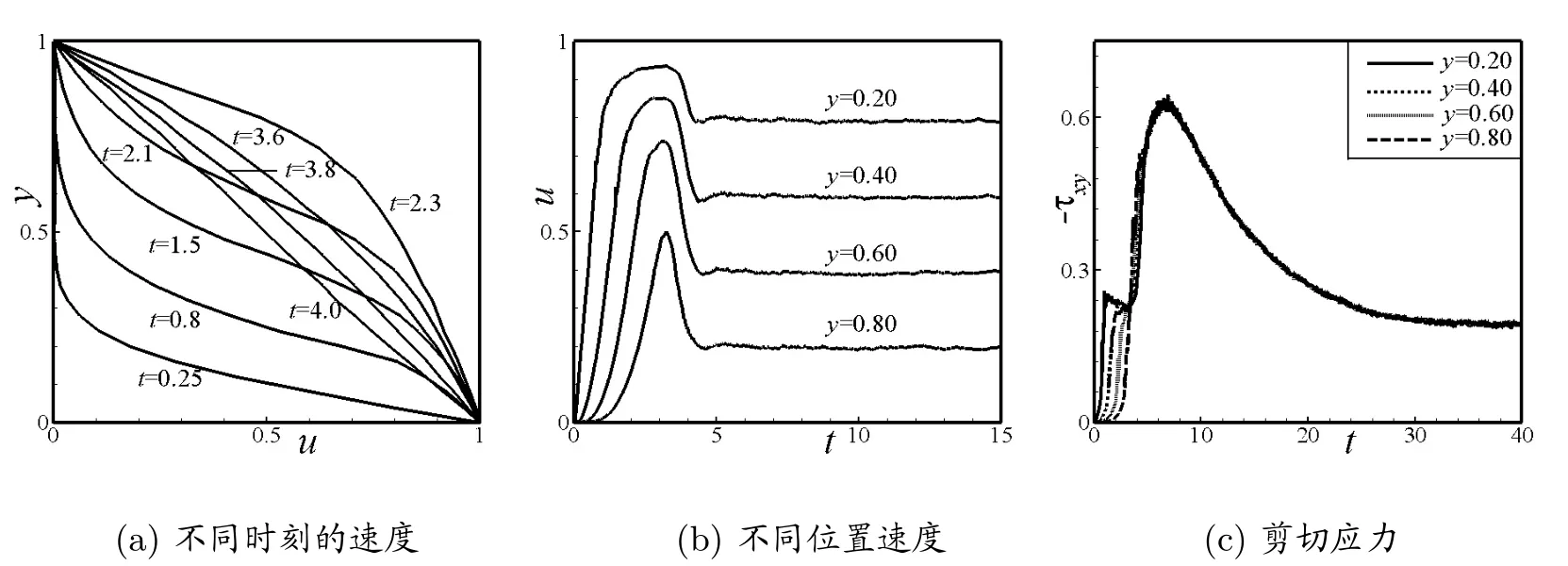
图3:平板Couette流速度和应力分布

5.2 平板收缩流

4:1平板收缩流能够反映流体经旋转、剪切和拉伸变形后的流动特性.收缩口附近存在的应力奇点，使流动问题的数值解在收缩口附近存在大梯度变化.因此，对4:1粘弹性收缩流动问题的模拟，更能检验本文数值方法的有效性.

同时，由于应力奇点的存在及FVMBCF方法在计算过程中不可避免地产生随机误差，导致在收缩口附近应力出现振荡.所以本节先给出施加方差缩减技术的FVMBCF方法的数值模拟结果，然后在5.3节给出关于施加方差缩减技术必要性的讨论.

由于收缩流的对称特性，仅选取图4所示y≥0的计算区域.将计算区域划分成四个部分，采用疏密不同的拼接网格.四个区域的网格分别取为：42×12、42×77、32×12和22×12.计算中固壁面边界满足无滑移边界条件.无量纲参数选取

收敛判定条件阈值5×10−5.入口速度为

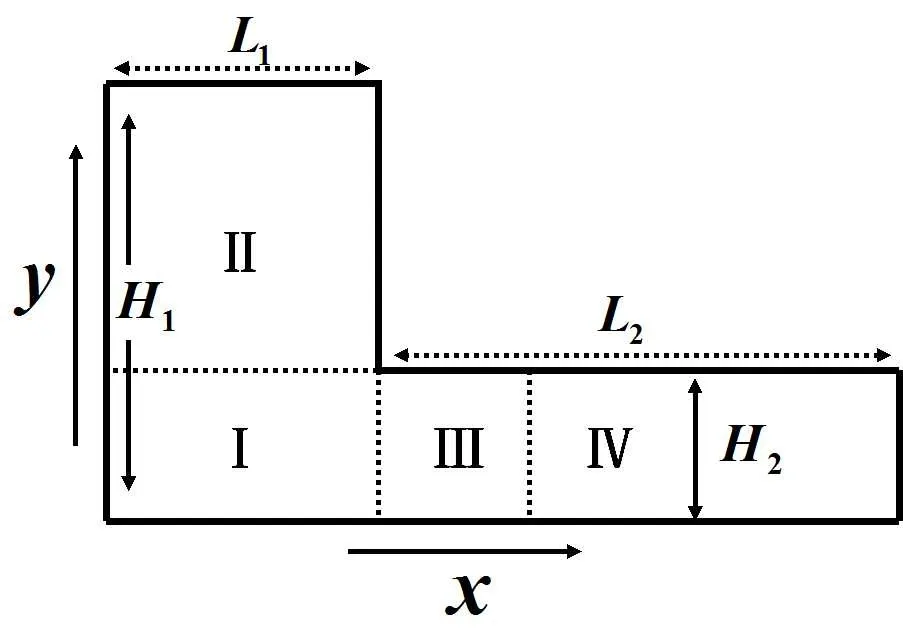
图4:收缩流动示意图

图5给出了不同We下收缩口附近的流线分布.由图5可知，在收缩口上游和下游处流动充分发展；在收缩口附近形成强拉伸区域；在上游拐角处，流动以旋转为主，形成角涡，且随着We的增大，涡流区的范围减小，涡心位置上升，角涡变小.

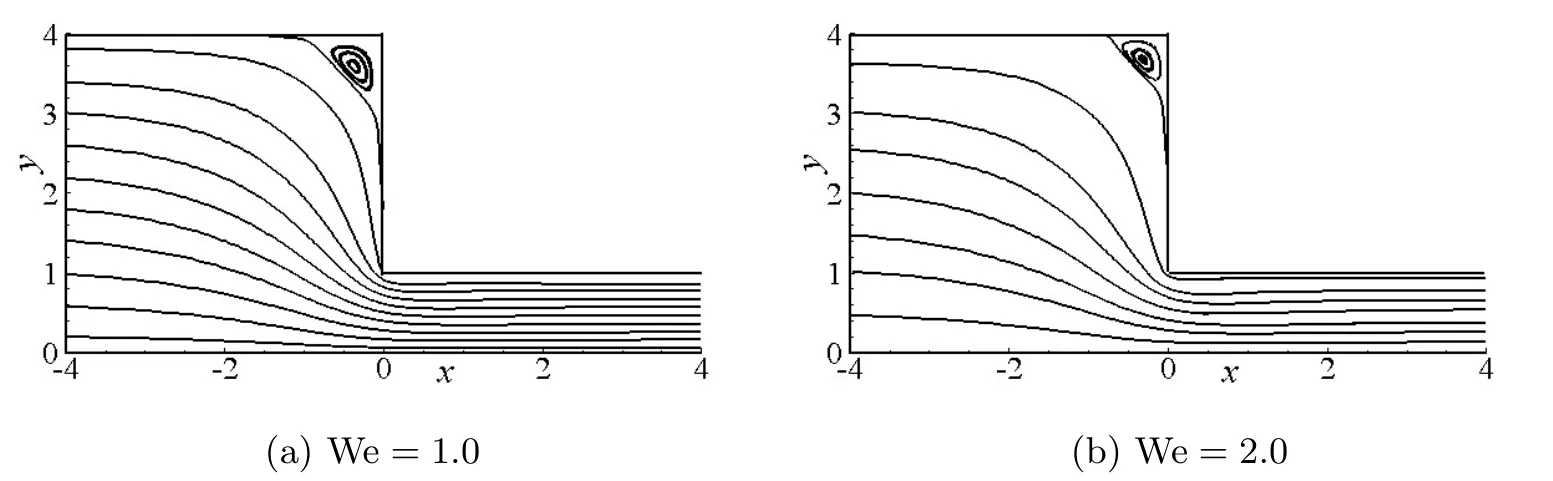
图5:不同We下收缩口附近的的流线分布

图6给出了We=1时收缩口附近的应力等值线分布.由图6可以看出，在收缩口附近，应力等值线光滑且分布密集，说明在收缩口处应力变化剧烈.图5与图6的数值结果与文献[12,13]相一致.

图6:We=1.0时收缩口附近的应力等值线分布

图7描述了流动稳定时收缩口附近y=1水平层面的速度、剪切应力及第一法向应力差的分布情况.由图7可知，随着We的增大，速度过冲现象更加明显.另外，剪切应力和第一法向应力差过冲现象加剧，收缩口附近的应力梯度很大，各应力分量均在收缩口附近取得最大值，且峰值随着We的增大而增加.这说明在收缩口附近，剪切拉伸作用随We的增大而加强.

图7:收缩口附近y=1的速度u、剪切应力τxy、第一法向应力差分布

5.3 方差缩减技术

图8描述了未施加及施加方差缩减技术情形下收缩口附近应力等值线的分布情况(左列是未施加方差缩减技术的结果，右列是施加方差缩减技术的结果).由图8可知，未施加方差缩减技术时，收缩口附近的应力等值线出现振荡现象；而施加方差缩减技术后，振荡现象消失，应力各分量等值线均变得光滑.这说明方差缩减技术能够很好地抑制收缩口附近的应力振荡.

图9给出了y=0.52位置处应力的数值结果，图中小方框内曲线是对收缩口附近(图中圆形区域)应力分布情形的放大处理.由图9可知施加方差缩减技术后应力的数值曲线较未施加的应力数值曲线光滑，振荡现象消失；但应力各分量的数值减小.这说明了FVMBCF方法施加方差缩减技术时具有能够确保获得光滑应力解的优点，但是同时存在着消弱应力解数值精度的缺陷.

图8:未施加及施加方差缩减技术情形下收缩口附近应力等值线的分布情况

图9:y=0.52位置处应力的数值结果

施加方差缩减技术时，由于控制变量参与计算，使得构形向量的总计算量将近增加一倍.但是模拟结果显示：同样基于四个并行进程，在选取相同收敛阈值的条件下，施加方差缩减技术的数值模拟耗时(57285.5s)比未施加方差缩减技术的数值耗时(56237.4s)仅多1.8%.这表明方差缩减技术能够在计算时间微量增加的条件下，很好地抑制应力的振荡现象，其稳定性能良好.

6 结束语

本文给出了施加方差缩减技术的FVMBCF方法及其求解流程，模拟了Couette流和4:1收缩流的粘弹性流动问题.数值结果表明：

1)该方法可以准确地模拟包含应力奇异点的复杂流动问题，计算结果可靠，算法易于实现；

2)该方法具有稳定性强和对流项处理简单的优点，且应力数值解具有光滑特性；

3)方差缩减技术能够很好地抑制收缩口附近的应力振荡现象.

参考文献：

[1]Abedijaberi A,Khomami B.Sedimentation of a sphere in a viscoelastic fluid:a multiscale simulation approach[J].Journal of Fluid Mechanics,2012,694(1):78-99

[2]Abedijaberi A,Khomami B.Continuum and multi-scale simulation of mixed kinematics polymeric flows with stagnation points:closure approximation and the high Weissenberg number problem[J].Journal of Non-Newtonian Fluid Mechanics,2011,166(11):533-545

[3]Owens R G,Phillips T N.Computational Rheology[M].London:Imperial College Press,2002

[4]陶文铨.数值传热学(第2版)[M].西安：西安交通大学出版社，2001 Tao W Q.Numerical Heat Transfer(2nd Edition)[M].Xi’an:Xi’an Jiaotong University Press,2001

[5]宋道云.同位网格有限体积法及其在粘弹性液体收缩流数值模拟中的应用研究[D].上海：华东理工大学，2002 Song D Y.The algorithm of collocated-grid finite volume method and its application of numerical simulation in a contraction flow for viscoelastic fluids[D].Shanghai:East China University of Science and Technology,2002

[6]代向艳，欧阳洁，张小华，等.基于Brown构形场的有限体积法在聚合物流动模拟中的应用[J].工程数学学报，2011,28(5):642-654 Dai X Y,Ouyang J,Zhang X H,et al.Simulation of the polymeric flows using finite volume method based on Brownian con figuration fields[J].Chinese Journal of Engineering Mathematics,2011,28(5):642-654

[7]代向艳，欧阳洁.平板Couette流场中聚合物流变性质及分子构象的数值模拟[J].高分子材料科学与工程，2011,27(3):157-161 Dai X Y,Ouyang J.Rheological properties and molecular con figuration of polymer solution in planar Couette flow[J].Polymer Materials Science and Engineering,2011,27(3):157-161

[8]张僡凤，欧阳洁，代向艳.耦合有限体积法的Brown构型场并行算法研究[J].计算物理学报，2012,29(1):17-24 Zhang H F,Ouyang J,Dai X Y.Paralle algorithm for Brownian con figuration fields with finite volume method[J].Chinese Journal of Computational Physics,2012,29(1):17-24

[9]Bonvin J,Picasso M.Variance reduction methods for CONNFFESSIT-like simulations[J].Journal of Non-Newtonian Fluid Mechanics,1999,84(2-3):191-215

[10]ttinger H C,van den Brule B,Hulsen M A.Brownian con figuration fields and variance reduced CONNFFESSIT[J].Journal of Non-Newtonian Fluid Mechanics,1997,70(3):255-261

[11]Tran-Canh D,Tran-Cong T.Element-free simulation of dilute polymeric flows using Brownian con figuration fields[J].Korea-Australia Rheology Journal,2004,16(1):1-15

[12]Aboubacar M,Webster M F.A cell-vertex finite volume/element method on triangles for abrupt contraction viscoelastic flows[J].Journal of Non-Newtonian Fluid Mechanics,2001,98(2-3):83-106

[13]Edussuriya S S,Williams A J,Bailey C.A cell-centred finite volume method for modelling viscoelastic flow[J].Journal of Non-Newtonian Fluid Mechanics,2004,117(1):47-61