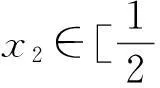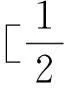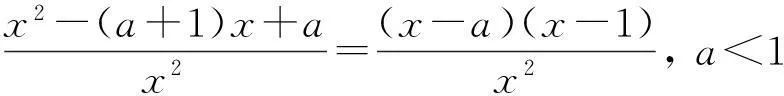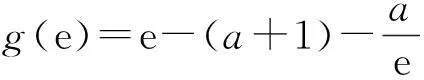聚集含参不等式恒成立问题

◇江苏汪小萍

本文就含参不等式恒成立问题加以归类解析,以帮助读者理清常用结论,理解、掌握常用解题思路、方法,不断提升求解此类问题的实际能力.

1含参一元二次不等式在R上恒成立问题

常用结论:

设二次函数f(x)=ax2+bx+c(a≠0),则

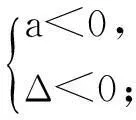
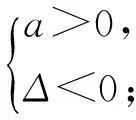
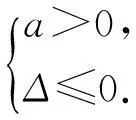
(1) 求a的值;

(2) 若|f(x)-2f(x/2)|≤k恒成立,求k的取值范围．

分析本题将分段函数及不等式相结合,并对绝对值不等式的应用进行了考查．主要目的在于考查学生分类思想在解题过程中的灵活应用．在第(1)问中,首先需针对a的取值情况进行分析.在第(2)题中,需针对f(x)-2f(x/2)的正负进行分析与讨论,从而利用分段函数进行表示,以此为依据求出k的取值范围．在解题过程中,需要准确掌握绝对值不等式的性质,并灵活运用．

解(1) 由|ax+1|≤3得-4≤ax≤2.又因为f(x)≤3的解集为{x|-2≤x≤1},因此,当a≤0时,不符合题意.

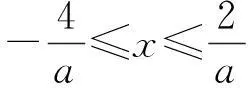
所以|h(x)|≤1,因此k≥1．

2含参不等式在某区间上恒成立问题

常用结论:

a>f(x)恒成立⟺a>fmax(x);

a≥f(x)恒成立⟺a≥fmax(x);

a

a≤f(x)恒成立⟺a≤fmin(x).

解对原函数求导得

3“任意、存在”型不等式恒成立问题

常用结论:

1) 若对任意x1∈D1,总存在x2∈D2,使得f(x1)

2) 若对任意x1∈D1,总存在x2∈D2,使得f(x1)>g(x2)(或f(x1)≥g(x2)),则函数f(x)在D1上的最小值大于(或大于等于)函数g(x)在D2上的最小值.

若对任意x1∈[-1,0],总存在x2∈[e,3],使得f(x1)>g(x2)成立,求实数a的取值范围.

分析解题关键在于,必须明确约束条件“对任意x1∈[-1,0],总存在x2∈[e,3],使得f(x1)>g(x2)成立”,等价于“函数f(x)在[-1,0]上的最小值大于函数g(x)在[e,3]上的最小值”.故需要先求得函数f(x)在[-1,0]上的最小值与函数g(x)在[e,3]上的最小值,然后再运用等价转化式即可获解.

解对任意x1∈[-1,0],总存在x2∈[e,3],使得f(x1)>g(x2)成立,等价于函数f(x)在[-1,0]上的最小值大于函数g(x)在[e,3]上的最小值.

当x∈[-1,0]时,f′(x)=x(1-ex)≤0,当且仅当x=0时不等式取等号,f(x)在[-1,0]上单调递减,f(x)在[-1,0]上的最小值为f(0)=1.

综上,遇到含参不等式恒成立问题时,我们应结合以上常用结论去考虑问题,以便迅速探求具体的解题思路.

(作者单位：江苏省扬州市广陵区红桥高级中学)