周　平,高美平，李艳艳

(文山学院数学学院,云南 文山 663000)



M-矩阵Hadamard积的新估计

周平,高美平，李艳艳

(文山学院数学学院,云南 文山 663000)

摘要：M-矩阵的Hadamard积是一种特殊的矩阵乘积，具有广泛的重要应用背景，概率统计、经济学、组合论、生物学和社会科学等领域中的许多问题都与它有着密切的联系，受到很多专家学者的关注和研究。首先介绍相关定义和性质，其次应用矩阵特征值包含域定理，结合非奇异M-矩阵的性质及其逆矩阵元素的特点，给出不同情形下2个M-矩阵的Hadamard积的最小特征值的几个新估计式。并用理论分析和算例表明新估计式在某些情况下比现有的估计结果更精确，给出的估计式改进了一些现有的结果。

关键词：M-矩阵；Hadamard积；最小特征值；估计式

1预备知识

设A=(aij)∈Rn×n,若aij≥0;i,j∈N,则称A为非负矩阵,记为A≥0；若aij>0;i、j∈N,则称A为正矩阵,记为A>0。设Zn⊂Rn×n表示非对角元非正的n×n实矩阵的集合。由矩阵A=(aij)∈Cn×n的所有特征值λ1,λ2,…,λn组成的集合称为A的谱,记为σ(A)；用q(A)表示A的最小特征值。ρ(A)=max{|λi|,i∈N}表示A的谱半径。

若A=(aij)∈Zn可表示为A=sI-P,其中P≥0,s≥ρ(P),则称A为M-矩阵。特别地,当s=ρ(P)时,称A为奇异M-矩阵；当s>ρ(P)时,称A为非奇异M-矩阵。记所有n×n阶非奇异M-矩阵所成之集为Mn。

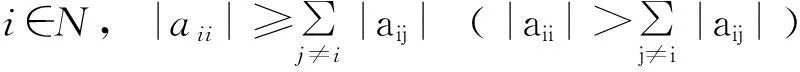
设A=(aij)∈Cm×n,B=(bij)∈Cm×n定义A·B=(aijbij)∈Cm×n，即

A·B称为A和B的Hadamard积,也称为Schur积。

本文讨论q(B·A-1)的下界。R.A.Horn在1991年给出如下估计式：

(1)

Huang Rong在2008年给出如下估计式：

(2)

在(1)式中要计算M-矩阵B的最小特征值，在(2)式中,要计算A和B的Jacobi迭代矩阵JA和JB的谱半径，如果矩阵的阶数较大时这些量都不容易计算出来。

Li Yaotang等在2010年给出如下估计式：

(3)

下面将给出q(B·A-1)的几个仅与矩阵A和B的元素有关的新估计式。

首先，为了叙述方便,先引入以下符号。

设A=(aij)∈Rn×n。如果A是可逆矩阵,那么记A-1=(βij),

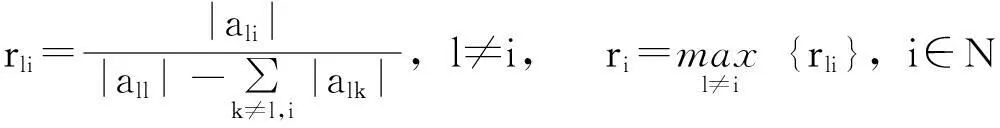
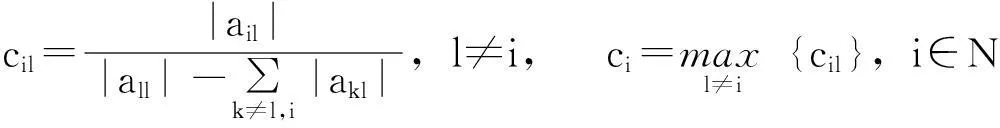
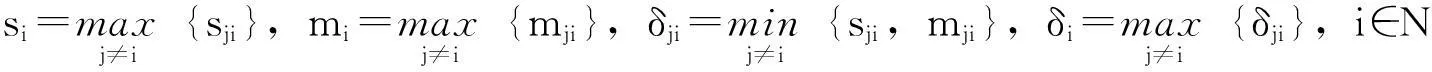
引理1若A∈Mn,Ak是A的主子矩阵，则q(Ak)≥q(A)；若A不可约且Ak≠A，则q(Ak)>q(A)。

引理2若A=(aij)∈Rn×n是一个严格行对角占优矩阵，则A-1=(βij)存在，且

引理3[4,7]若A=(aij)∈Mn是一个严格行对角占优M-矩阵,则A-1=(βij)存在且有

引理4若A=(aij)∈Mn，且A-1=(βij)是双随机矩阵，则

引理5若A=(aij)∈Cn×n,G是N={1,2,…,n)(n≥2)的任意非空真子集,则矩阵的所有特征值包含在如下集合中

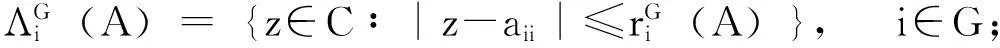
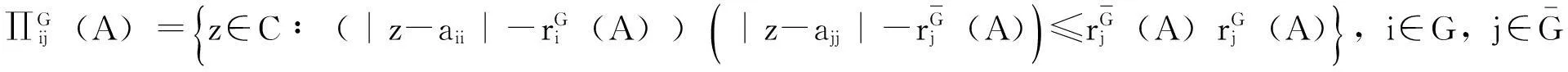
2主要结论

定理1设A=(aij)∈Rn×n是严格行对角占优M-矩阵,B=(bij)∈Mn,A-1=(βij),则

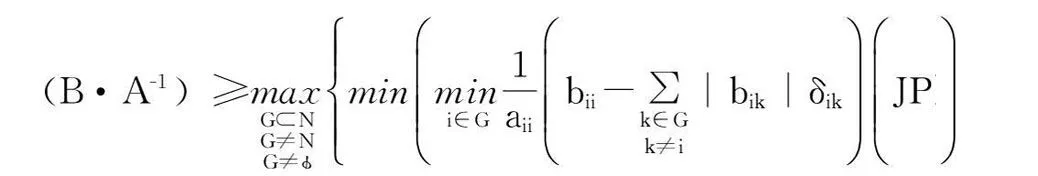
证明：令C=B·A-1=(cij)，根据引理1知，任取i∈N，有cii-q(C)>0。记λ=q(B·A-1)。设 G⊂N且G≠N，G≠φ，应用引理5得

(ⅰ)存在某个i∈G，使得

即

故

(4)

应用引理2，则(4)式得

(5)

应用引理3，则(5)式得

即

(6)

即

故

即

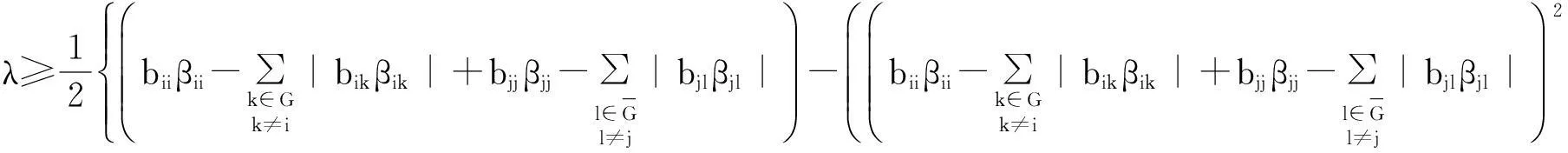
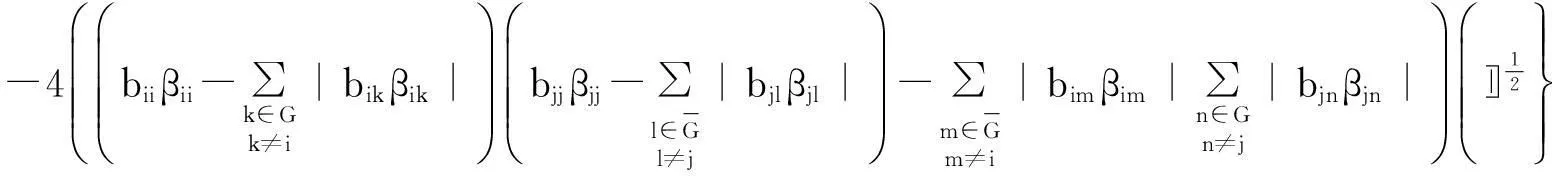
(7)

应用引理2和引理3，则(7)式得

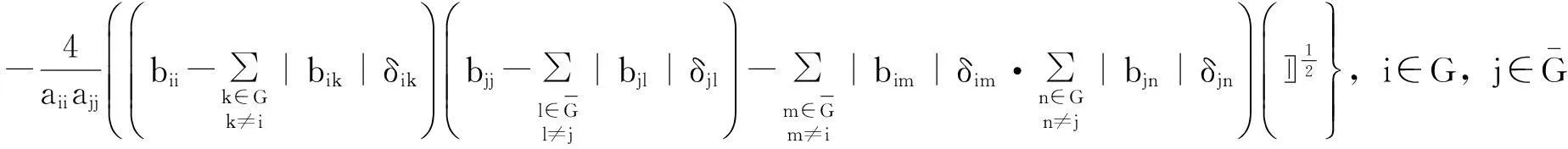
即

根据上述论证，由(ⅰ)(ⅱ)知

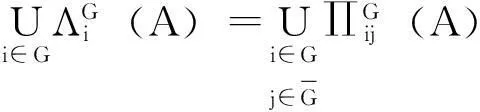
定理2设A=(aij),B=(bij)∈Mn,A-1=(βij),则

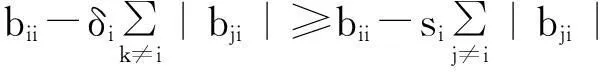
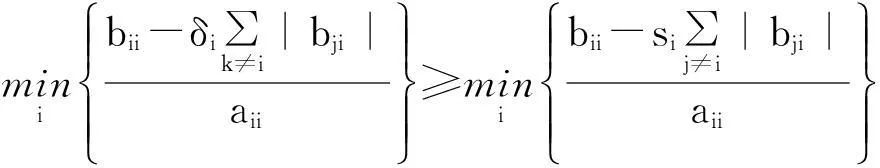
注2根据注释1和定理2的证明便知，文中定理1改进了已有的结果。

当A=B时，应用定理1可得到下面的推论。

推论1设A=(aij)∈Rn×m为严格行对角占优M-矩阵,A-1=(βij),则

当A-1是双随机矩阵时，可得到下面的结果。

定理3设A=(aij),B=(bij)∈Mn,且A-1=(βij)是双随机矩阵，则

证明：令E=B·A-1=(eij)，根据引理1知，任取i∈N，有eii-q(E)>0。记λ=q(B·A-1)。设H⊂N且H≠N,H≠φ，应用引理5得

(Ⅰ)存在某个i∈H,使得

即

故

(8)

应用引理2，则(8)式得

(9)

应用引理4，则(9)式得

即

(10)

即

故

即

(11)

应用引理2和引理4，则(11)式得

即

综合上述(Ⅰ)(Ⅱ)得

3数值例子

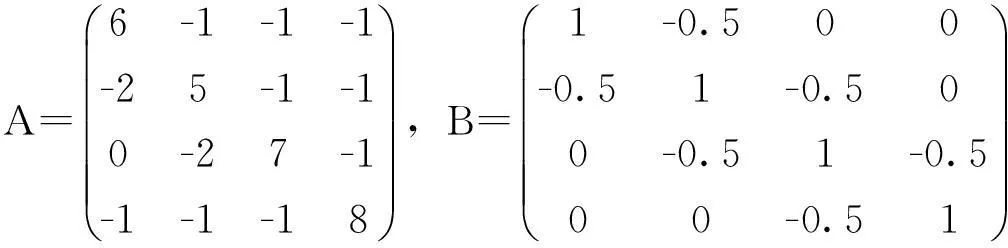
显然A，B∈Mn，且A是严格行对角占优矩阵，应用Matlab计算得q(B·A-1=0.128 5。应用(2)式计算得q(B·A-1)≥0.026 8；应用(3)式计算得q(B·A-1≥0.055 5；应用(4)式计算得q(B·A-1≥0.071 4；应用文献中定理2.1计算得q(B·A-1)≥0.109 3。而由本文给出的定理1得q(B·A-1)≥0.117 3。

4结论

对上述例子的计算结果进行比较可知，文中对q(B·A-1)的下界的估计比文献[2～4,6]的估计更精确，且只与矩阵的元素有关，更容易计算。

参考文献：

[1]黄廷祝,杨传胜.特殊矩阵分析及应用.北京:科学出版社,2003：15-27.

[2]Horn R A,Johnson C R.Topic in Matrix Analysis.New York：Cambridge University Press,1991：103-124.

[3]Huang R.Some inequalities for the Hadamard product and the Fan product of matrices.Linear Algebra Appl,2008,428:1551-1559.

[4]Li Y T,Li Y Y,Wang R W,et al.Some new bounds on eigenvalues of the Hadamard product and the Fan product of matrices.Linear Algebra Appl,2010,432:536-545.

[5]Berman A,Plemmmons R J.Nonnegative matrices in the mathematical sciences.SIAM,1994,101:1068-1072.

[6]Chen F B.Some new inequalities for the Hadamard product M-matrices.Inequ Appl,2013,581:1-10.

[7]Li Y T,Chen F B,Wang D F.New lower bounds on eigenvalue of the Hadamard product of an matrix and inverse.Linear Algebra Appl,2009,430：1423-1431.

[8]Cvetkovic L. H-matrix theory vs.eigenvalue localization.Numer Algor,2006,42:229-245.

[责任编辑：郑秀亮英文编辑：刘彦哲]

New Estimations of Hadamard Product ofM-matrices

ZHOU Ping,GAO Mei-ping，LI Yan-yan

(School of Mathematics,Wenshan University，Wenshan，Yunnan 663000，China)

Abstract:The Hadamard product of M-matrices is a special kind of multiplication on matrices,which has a widely important range of application background.Some problems have a strong association with it in the fields of probability and statistics,economics,combinatorial theory,biology and the social sciences.It has been concerned with research by many experts and scholars.Many definitions and properties are introduced.Then the theorem for localizations of Matrix eigenvalues is used,combining with some properties of nonsingular M-matrices and characteristics of its inverse elements.Hadamard product of two M-matrices is further researched in different situations,and some new estimations of smallest eigenvalue are given.Theoretical analysis and numerical figure showed that these inequalities are more exact than some of the current results in some cases.The estimations obtained improve the existing results.

Key words:M-matrix;Hadamard product;smallest eigenvalue;estimation

DOI：10.3969/j.issn.1673-1492.2016.01.001

中图分类号：O 151.21

文献标识码：A

作者简介：周平(1987-)，女，云南永平人，讲师，硕士，主要从事数值代数和矩阵理论及其应用研究。

基金项目：国家自然科学基金支助项目(11261049)；云南省科技厅应用基础研究项目(2013FD052)；文山学院重点学科“数学”建设项目(12WSXK01)

来稿日期：2015-12-16