杨义先，钮心忻

(北京邮电大学 信息安全中心，北京 100083)

安全通论(8)
——黑客篇之“战略研究”

杨义先，钮心忻

(北京邮电大学 信息安全中心，北京 100083)

编者按：对技术水平有限的(经济)黑客来说，如何通过“田忌赛马”式的组合攻击策略来实现“黑产收入”最大化呢？是否存在这种最优的攻击组合呢？本文作者借助股票投资领域中的相关思路和方法，得到了一些有趣的结果。比如，给出了黑客同时攻击m个系统的对数最优攻击组合策略，它不但能使黑客的整体收益最大化，而且能够使每轮攻击的收益最大化；如果采用对数最优的攻击组合策略，那么黑客攻击每个系统的“投入产出比”不会在本轮攻击结束后发生变化；如果黑客还能够通过其他渠道获得一些“内部消息”，那么他因此多获得“黑产收入”的增长率不超过“被攻击系统的“投入产出比”与“内部消息”之间的互信息”；如果随时间变化的被攻击系统是平稳随机过程，那么黑客的最优攻击增长率是存在的。所得结论是，熵越小的黑客攻击策略，所获得的“黑产收入”越大。阅读原文可登录科学网：http://blog.sciencenet.cn/blog_453322_950146.html。

杨义先

教授，博士生导师，灾备技术国家工程实验室主任，北京邮电大学信息安全中心主任，教育部网络攻防重点实验室主任，《微型机与应用》编委，主要研究方向：网络空间安全、现代密码学和纠错编码等。

钮心忻

博士，教授，博士生导师。北京邮电大学学士和硕士学位，香港中文大学电子工程系博士学位。1997年起在北京邮电大学信息工程学院(现计算机学院)从事教学与科研工作。主要研究方向：网络与信息安全、信号与信息处理等。

0 引言

由于政治黑客后台很硬，不计成本，不择手段，耐得住寂寞，因此，从纯技术角度看，政治黑客是最牛的黑客，他们的攻击力远远超过经济黑客等普通黑客。

为了量化分析(因为政治问题无法量化)，参考文献[1]不得不用“宰牛刀”来“杀鸡”(即用政治黑客的技术来为经济黑客的利益服务)，给出了最牛黑客的完整静态描述，并且给出了他们的最佳组合攻击战术。但是，并不是所有黑客都能够达到如此高的技术极限，甚至这样的黑客也许可望而不可及。

幸好，经济黑客的主要目标是获取最大的“黑产收入”，而不是要伤害被攻击系统(政治黑客刚好相反，他的目标是伤害对方，而非获得经济利益)，当然，经济黑客也不会有意去保护对手。所以，经济黑客的技术水平虽然有限，但是，他们可以依据已有的技术水平，像“田忌赛马”那样，通过巧妙地“组合攻击”来尽可能实现收益最大化。

黑客攻击和炒股其实很相像。实际上，政治黑客的攻击就像“庄家炒股”，虽然他对被攻击系统(待炒的股票)的内部情况了如指掌，但是，他的期望值也很高，不出手则已，一旦出手就要摧毁目标(赚大钱)，因此，一旦行动起来，其战术就非常重要，不能有任何细节上的失误，否则前功尽弃。事实证明，“庄家炒股”也有赔钱的时候，同样，政治黑客的攻击也有失手的时候，基本上都是输在战术细节上。

经济黑客的攻击就像“散户炒股”，虽然整体上处于被动地位，资金实力也很差，但是自身的期望值并不很高，只要有钱赚，哪怕刚够喝稀饭。经济黑客的攻击(散户的炒股)当然不能靠硬拼，必须讲究战略，比如：(1)正确选择被攻击系统(待炒的股票)，若目标选错了，当然要赔本；(2)合理分配精力去攻击所选系统(炒作所选股票)，既不要“在一棵树上吊死”，也不能“小猫钓鱼”(既不能把资金全部投到某一支股票，也不要到处“撒胡椒粉”)。事实证明，散户炒股也有赢钱的时候，只要他很好地运用了相关战略(即选股选对了，在每支股票上的投资额度分配对了)。同样，如果经济黑客正确地把握了相关战略,他也有可能获利。本文将给出一些确保黑客获利的“对数最优”战略，当然，本文的结果也可帮助散户股民炒股，前提是他们能够读懂此文(我相信普通的经济黑客是可以读懂此文的)。

过去若干年以来，人们已经在投资策略(包括炒股)方面进行了大量研究，并由此丰富了博弈论的内容。本文的许多思想、方法和结果也是来源于这些理论。

1 对数最优攻击组合

设黑客想通过攻击某m个系统来获取其经济利益，并且根据过去的经验，他攻击第i个系统的“投入产出比”是随机变量Xi(≥0,i=1,2,…,m)，即攻击第i个系统时，若投入1元钱，则其收益是Xi元钱。记收益列向量X=(X1,X2,…,Xm)T服从联合分布F(x)，即，X～F(x)。

从经济角度看，所谓黑客的一个攻击组合，就是一个列向量b=(b1,b2,…,bm)T,bi≥0, ∑bi=1，它意指该黑客将其“用于攻击的资金总额”的bi部分，花费在攻击第i个系统上(i=1,2,…,m)。于是，在此组合攻击下，黑客的收益便等于S=bTX=∑i=1mbiXi。S显然也是一个随机变量。

当本轮组合攻击完成后，黑客还可以发动第2轮、第3轮等组合攻击，即黑客将其上一轮结束时所得到的全部收益按相同比例b分配，形成新一轮的攻击组合b。下面将努力寻找最佳的攻击组合b，使得经过n轮组合攻击后，黑客的收益S在某种意义上达到最大值。

定义1：攻击组合b关于收益分布F(x)的增长率，定义为：

W(b,F)=∫log(bTx)dF(x)=E[log(bTX)]

如果该对数的基底是2，那么，该增长率W(b,F)就称为双倍率(见参考文献[1])。攻击组合b的最优增长率W*(F)定义为：

W*(F)=maxbW(b,F)

这里的最大值遍取所有可能的攻击组合b=(b1,b2,…,bm)T,bi≥0, ∑bi=1。如果某个攻击组合b*使得增长率W(b,F)达到最大值，那么，这个攻击组合就称为“对数最优攻击组合”。

为了简化上角标，本文对b*和b(*)交替使用，不加区别。

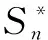
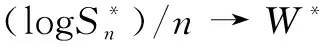
证明：由强大数定律可知：

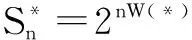
引理1：W(b,F)关于b是凹函数，关于F是线性的，而W*(F)关于F是凸函数。

证明：增长率公式为W(b,F)=∫log(bTx)dF(x)，由于积分关于F是线性的，因此，W(b,F)关于F是线性的。又由对数函数的凸性可知：

(1-λ)log(b2TX)

对该公式两边同取数学期望，便推出W(b,F)关于b是凹函数。最后，为证明W*(F)关于F是凸函数，假设F1和F2是收益列向量的两个分布，并令b*(F1)和b*(F2)分别是对应于两个分布的最优攻击组合。令b*(λF1+(1-λ)F2)为对应于λF1+(1-λ)F2的对数最优攻击组合，那么，利用W(b,F)关于F的线性特性，有：

W*(λF1+(1-λ)F2)

=W*[b*(λF1+(1-λ)F2), λF1+(1-λ)F2]

=λW*[b*(λF1+(1-λ)F2),F1]+(1-λ)W*[b*(λF1+(1-λ)F2),F2]

≤λW*[b*(F1),F1]+(1-λ)W*[b*(F2),F2]

因为b*(F1)和b*(F2)分别使得W(b,F1)和W(b,F2)达到最大值。证毕。

引理2：关于某个分布的全体对数最优攻击组合构成的集合是凸集。

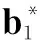
W[λb1+(1-λ)b2,F]≥λW(b1,F)+(1-λ)W(b2,F)=W*(F)

也就是说，λb1+(1-λ)b2还是一个对数最优的攻击组合。证毕。

定理2：设黑客欲攻击的m个系统的收益列向量X=(X1,X2,…,Xm)T服从联合分布F(x)，即X～F(x)，那么，该黑客的攻击组合b*是对数最优(即使得增长率W(b,F)达到最大值的攻击组合)的充分必要条件是：

证明：由于增长率W(b)=E[log(bTX)]是b的凹函数，其中b的取舍范围为所有攻击组合形成的单纯形。于是，b*是对数最优的，当且仅当W(·)沿着从b*到任意其他攻击组合b方向上的方向导数是非正的。于是，对于0≤λ≤1，令bλ=(1-λ)b*+λb，可得：

[dW(bλ)/dλ]│λ=0+≤0，b∈В

由于W(bλ)在λ=0+处的单边导数为：

=limλ→0{E[log[[(1-λ)b*TX+λbTX]/[b*TX]]]}/λ

=E{limλ→0{[log[1+λ[(bTX)/(b*TX)-1]]]/λ}}

=E[(bTX)/(b*TX)]-1

这里λ→0表示从正数方向趋向于0。于是，对所有b∈В都有：E[(bTX)/(b*TX)]-1≤0。如果从b到b*的线段可以朝着b*在单纯形В中延伸，那么W(bλ)在λ=0点具有双边导数且导数为0，于是，E[(bTX)/(b*TX)]=1；否则，E[(bTX)/(b*TX)]<1(注：此定理的更详细证明可参考文献[1]的定理16.2.1的证明过程)，证毕。

由上面的定理2，可以得出如下推论：

定理3：设S*=b*TX是对应于对数最优攻击组合b*的黑客收益，令S=bTX是对应于任意攻击组合b的随机收益，那么，对所有的S有E[log(S/S*)]≤0 当且仅当对所有S有E(S/S*)≤1。

证明：对于对数最优的攻击组合b*，由定理2可知，对任意i有E[Xi/(b*TX)]≤1。对此式两边同乘以bi，并且关于i求和，可得到：

这等价于E[(bTX)/(b*TX)]=E(S/S*)≤1，因为E[log(S/S*)]≤log[E(S/S*)]≤log1=0，其逆可由Jensen不等式得出，证毕。

此定理表明，对数最优攻击组合不但能够使得增长率最大化，而且，也能使得每轮攻击的收益比值E(S/S*)最大化。

因此，第i个系统在本轮攻击结束后的收益占整个攻击组合收益的比例的数学期望值，与本轮攻击开始时第i个系统的攻击投入比例相同。一旦选定按比例进行攻击组合，那么在期望值的意义下，该攻击组合比例将保持不变。

现在深入分析定理1中n轮攻击后黑客的收益情况。令

W*=maxbW(b,F)=maxbE(log(bTX))

为最大增长率，并用b*表示达到最大增长率的攻击组合。

定义2：一个因果的攻击组合策略定义为一列映射bi:Rm(i-1)→В，其中bi(x1,x2,…,xi-1)解释为第i轮攻击的攻击组合策略。

由W*的定义可以直接得出：对数最优攻击组合使得最终收益的数学期望值达到最大。

引理3：设Sn*为定理1所指的在对数最优攻击组合b*之下n轮攻击后黑客的收益。又设Sn为采用定义2中的因果攻击组合策略bi在n轮攻击后黑客的收益。那么，E(logSn*)=nW*≥E(logSn)。

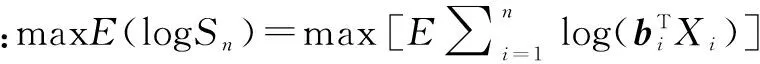
到此就知道：由定理2中的b*给出的攻击组合能够使得黑客收益的期望值达到最大值，而且所得的收益Sn*以高概率在一阶指数下等于2nW(*)。其实还可以得到如下更强的结论。

定理4：设Sn*和Sn如引理3所述，那么依概率1有，

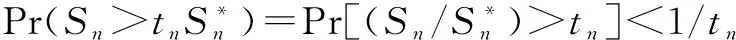
取tn=n2，并对所有n求和，得到：

利用Borel-Cantelli引理得：

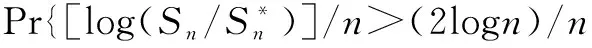
该定理表明，在一阶指数意义下，对数最优攻击组合的表现相当好。

散户炒股都有这样的经验：如果能够搞到某些“内部消息”(学术上称之为“边信息”)，那么炒股赚钱的可能性就会大增；但是，到底能够增加多少呢？下面就来回答这个问题。当然，这里将其叙述为：边信息对黑客收益的可能影响。

定理5：设X服从分布f(x)，而bf为对应于f(x)的对数最优攻击组合。设bg为对应于另一个密度函数g(x)的对数最优攻击组合。那么采用bf替代bg所带来的增长率的增量满足如下不等式：ΔW=W(bf,F)-W(bg,F)≤D(f|g)。这里，D(f|g)表示相对熵(见参考文献[1])。

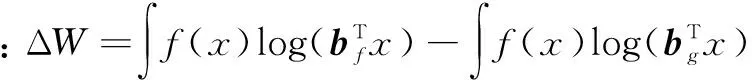
≤log1+D(f|g)=D(f|g)。证毕。

定理6：由边信息Y所带来的增长率的增量ΔW满足不等式：ΔW≤I(X;Y)。这里I(X;Y)表示随机变量X与Y之间的互信息。

证明：设(X,Y)服从分布f(x,y)，其中X是被攻击系统的“投入产出比”向量，而Y是相应的边信息。当已知边信息Y=y时，黑客采用关于条件分布f(x|Y=y)的对数最优攻击组合，从而在给定条件Y=y下，利用定理5，可得：

ΔWY=y≤D[f(x|Y=y)│f(x)]

=∫xf(x|Y=y)log[(f(x|Y=y))/f(x)]dx

对Y的所有可能取值进行平均，得到：

ΔW≤∫yf(y){∫xf(x|Y=y)log[(f(x|Y

=y))/f(x)]dx}dy=∫y∫xf(y)f(x|Y=y)log[(f(x|Y

=y))/f(x)][f(y)/f(y)]dxdy

=∫y∫xf(x,y)log{f(x,y)/[f(x)f(y)]}dxdy=I(X;Y)

从而，边信息Y与被攻击的系统向量序列X之间的互信息I(X;Y)是增长率的增量的上界。证毕。

该定理6形象地说明，“内部消息”能够使黑客的“黑产收益”增长率的精确上限不超过I(X;Y)。

下面再考虑被攻击系统依时间而变化的情况。

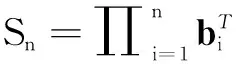
W*(X1,X2,…,Xn)=maxbElogSn

该链式法则在形式上与熵函数H的链式法则完全一样(见文献[1])。确实，在某些方面W与H互为对偶，特别地，条件作用使H减小，而使W增长，换句话说：熵H越小的黑客攻击策略所获得的“黑产收入”越大。

定义3(随机过程的熵率)：如果存在如下极限：

定理7：如果黑客“投入产出比”形成的随机过程X1，X2，…，Xn，…为平稳随机过程，那么黑客的最优攻击增长率存在，并且等于

证明：由随机过程的平稳性可知，W*(Xn|X1,X2,…,Xn-1)关于n是非减函数，从而其极限是必然存在的，但是有可能是无穷大。由于

证毕。

在平稳随机过程的情况下，还有如下的渐近最优特性。

2 结束语

至此，《安全通论》的三块基石(安全经络、安全攻防、黑客本质)就基本奠定。

接下来将努力探索《安全通论》的另一个重要篇章，即第四块基石：红客篇。虽然，红客是被黑客逼出来的，但是，毕竟红客是“女一号”(如果把黑客看成“男一号”的话)，因此，也需要对其进行深入研究。

到现在为止，《安全通论》的基本架构已经显现出来了。当然，还有许多更细致的工作要做，特别是，如何用《安全通论》去指导网络空间安全的技术与实践，即要使《安全通论》“落地”，这当然需要安全界全体同仁的共同努力。

回过头来考查《安全通论》(1)～(7)时发现了一个很奇怪的现象，即在《安全通论》的全部成果中[2-8]总有一个“幽灵”始终挥之不去。这个“幽灵”便是“熵”。其实，在《安全通论》的研究过程中并未刻意依赖(或回避)“熵”，但是，这个“熵”却总是要主动跳出来，这到底是为什么呢？是必然还是偶然？

下面试图来回答这个问题，特别是把“熵”和老子的“道”[9]放在一起进行比较。

“熵”是什么？在化学及热力学中，“熵”是“在动力学方面不能做功的能量”；最形象的“熵”定义为“热能除以温度”，它标志热量转化为功的程度。在自然科学中，“熵”表示系统的不确定(或失序)程度。在社会科学中，“熵”用来借喻人类社会某些混乱状态的程度。在传播学中，“熵”表示情境的不确定性和无组织性。根据文献[2]，“安全”也是一种“负熵”，或“不安全”是一种“熵”。在信息论中，“熵”表示不确定性的量度，即“信息”是一种“负熵”，是用来消除不确定性的东西。总之，“熵”存在于一切系统之中，而且在不同的系统中，其表现形式也各不相同。其实，老子的“道”(见文献[9])也是这样的，即，天地初之“道”，称为“无”；万物母之“道”，称为“有”；“有”与“无”相生。“道”体虚空，功用无穷；“道”深如渊，万物之源；“道”先于一切有形。“道”体如幽悠无形之神，是最根本的母体，也是天地之本源。“道”隐隐约约，绵延不绝，用之不竭。“道”具无形之形，无象之象，恍恍惚惚；迎面不见其首，随之不见其后。幽幽冥冥，“道”中有核，其核真切，核中充实。对“道”而言，尝之无味，视之无影，听之无声，但是，却用之无穷。天得道，则清静；地得道，则安宁；神得道，则显灵；虚谷得道，则流水充盈；万物得道，则生长；侯王得道，则天下正。“道”很大，大得无外；“道”很小，小得无内。

“熵”都有哪些特点？在热力学中，“熵”的特征由热量表现，即热量不可能自发地从低温物体传到高温物体；在绝热过程中，系统的“熵”总是越来越大，直到“熵”值达到最大值，此时系统达到平衡状态。从概率论的角度来看，系统的“熵”值直接反映了它所处状态的均匀程度，即系统的熵值越小，它所处的状态就越有序，越不均匀；系统的熵值越大，它所处的状态就越无序，越均匀。系统总是力图自发地从熵值较小的状态向熵值较大(即从有序走向无序)的状态转变，这就是封闭系统“熵值增大原理”。从社会学角度来看，“熵”就是社会生存状态及社会价值观，它的混乱程度将不断增加；现代社会中恐怖主义肆虐、疾病疫病流行、社会革命和经济危机爆发周期缩短、人性物化等都是社会“熵”增加的表征。从宇宙论角度看，“熵”值增大的表现形式是：在整个宇宙当中，当一种物质转化成另外一种物质之后，不仅不可逆转物质形态，而且会有越来越多的能量变得不可利用，宇宙本身在物质的增殖中走向“热寂”，走向一种缓慢的“熵”值不断增加的死亡。总之，“熵”的有效性始终在不断地减少，这是一种“反动”，与“道者反之动”完全吻合，即“道”被荒废后，才出现仁义。智慧出来后，才滋生伪诈。六亲不和，才倡导孝慈。国家昏乱，才需要忠臣。失“道”后，才用德；失德后，才用仁；失仁后，才用义；失义后，才用礼；失礼后，才用法。

若将物质看成“道体”，将能量看成“道用”，将熵看成“道动”，那么老子在2 500年前撰写的《道德经》就已活灵活现地描绘了宇宙大爆炸学说。因此，我们再结合宇宙爆炸学说，对比一下老子的“道”：“道”是一种混沌物，它先天地而生，无声无形，却独立而不改变；周而复始不停息。它可做天地之母，“道”在飞速膨胀，膨胀至无际遥远；远至无限后，又再折返。“道”生宇宙之混沌元气，元气生天地，天地生阳气、阴气、阴阳合气，合气生万物。

综上所述，“熵”在哲学中就变为“道”；“道”在科学中，就变成“熵”。由于“道生一，一生二，二生三，三生万物”，即“道”能生万物，那么“道”生《安全通论》也就名正言顺了。这也许就是“熵”的身影在《安全通论》中始终挥之不去的根本原因吧。

[1]COVERTM，THOMASJA.信息论基础[M]. 阮吉寿，张华,译.北京：机械工业出版社,2007.

[2] 杨义先，钮心忻，安全通论(1)——经络篇[J].微型机与应用，2016，35(16)：1-4.

[3] 杨义先，钮心忻.安全通论(2)——攻防篇之“盲对抗”[J].微型机与应用，2016，35(16)：1-5.

[4] 杨义先，钮心忻.安全通论(3)——攻防篇之“非盲对抗”之“石头剪刀布”[J].微型机与应用，2016，35(17)：1-3.

[5] 杨义先，钮心忻，安全通论(4)——攻防篇之“非盲对抗”之“童趣游戏”[J].微型机与应用，2016，35(18)：1-4.

[6] 杨义先，钮心忻，安全通论(5)——攻防篇之“非盲对抗”之“劝酒令”[J].微型机与应用，2016，35(19)：2-6.

[7] 杨义先，钮心忻，安全通论(6)——攻防篇之“多人盲对抗” [J].微型机与应用，2016，35(20)：1-4.

[8] 杨义先，钮心忻，安全通论(7)——黑客篇之“战术研究”[J].微型机与应用，2016，35(21)：1-4.

[9] 杨义先，最形似的《道德经》[EB/OL].(2014-11-22)[2016-02-25]http://blog.sciencenet.cn/blog-453322-845400.html.

(未完待续，系列之九《安全通论(9)——红客篇》见下期)