陈春玲，齐年强，余 瀚

(南京邮电大学 计算机学院，江苏 南京 210003)

RSA算法的研究和改进

陈春玲，齐年强，余 瀚

(南京邮电大学 计算机学院，江苏 南京 210003)

为了提高RSA算法的安全性，避免RSA密码体制中的模n被因子分解，导致私钥d泄露，采取消除密钥中n的分布方法以及对三个因素因子的加密方法。采用消除密钥中n的分布方法可以成功避免在公布的公钥和保密的私钥中出现n，防止攻击者通过因子分解法分解出公钥中n的因子，推导出解密密钥d；采用三因子的加密算法，即使攻击者知道了φ(n)，但对于分解n的三个素数没有一个具体的公式，所以加大了分解的困难性，并且因为大素数适当减小了位数，降低了计算量。实验结果表明，该方法提高了RSA算法的安全性，时间复杂度与传统RSA算法相同。

RSA；安全性；公钥；私钥；时间

0 引 言

在RSA算法中两个密钥之间存在一种数学上的联系。基于这个事实，如果某个人发现了这种数学联系并成功获取了私钥，这样体制就会被破坏。算法中公钥和私钥都包含大数n，n可以被分解为因子p和q。众所周知，公钥是公开的，因此，如果某人猜到了n的因子那就很容易获取私钥。为了阻止该事件的发生，算法中尝试消除私钥和公钥中n的分布，在n上运用一种数学变换，通过使用X来替代n，使得攻击者无法分解到n的因子。文中同时提出了三因子的RSA加密算法，指的是选取三个素数因子a1、a2、a3，它们的乘积为n，即n=a1×a2×a3。该算法可以降低大素数选择所需要的时间，适当地减少大素数的位数，降低计算量。

1 传统RSA密码算法的研究与分析

RSA算法[1]是1978年由三位数学家Rivest、Shamir和Adleman根据Whitfield与Martin Hellman的理论框架设计出的一种非对称加密算法。RSA密码体制的安全性取决于其加密算法的数学函数的求逆困难性，称之为大数因子分解的困难性[2-4]。RSA包含了产生密钥、加密信息和解密信息三个步骤：

步骤1：产生密钥。

选取两个大素数p和q，p≠q。计算乘积：

n=p×q

(1)

得到欧拉函数：

φ(n)=(p-1)×(q-1)

(2)

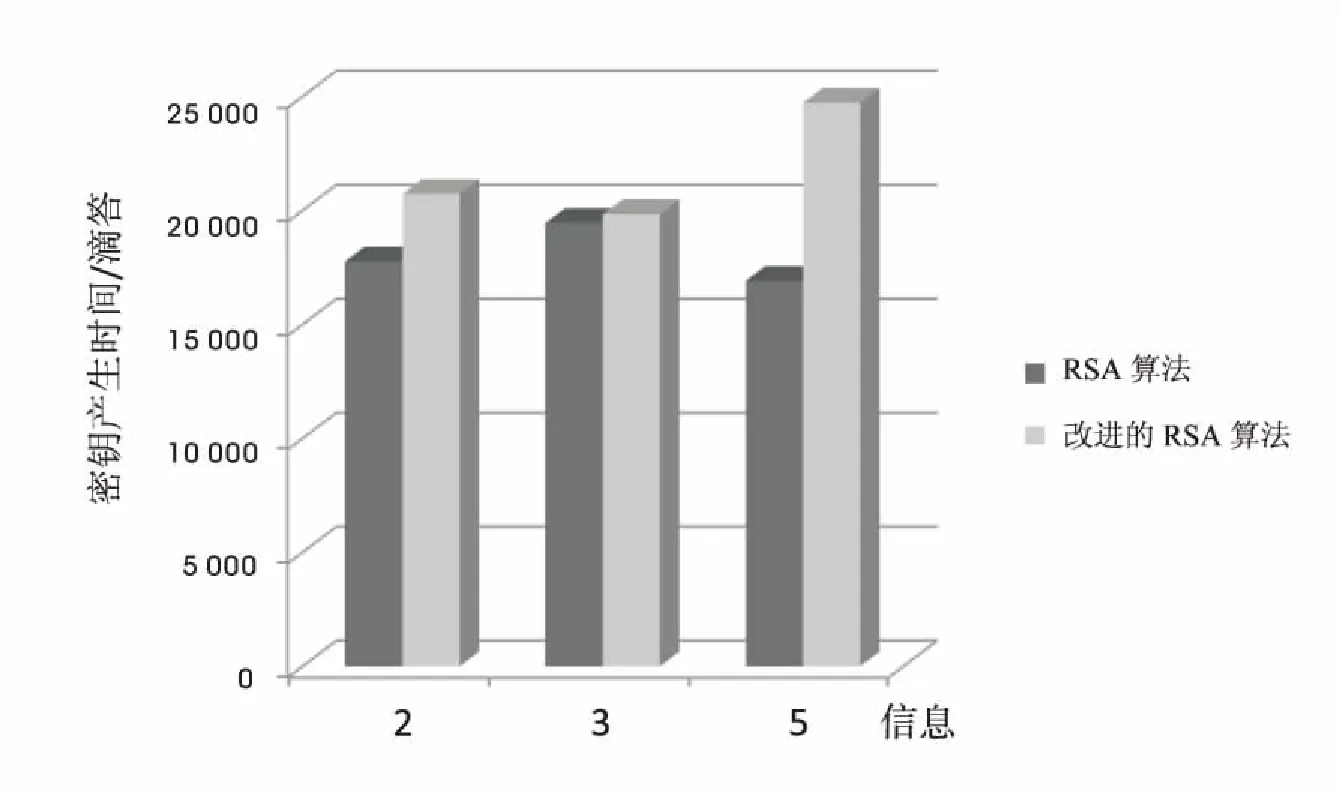
选择随机整数e，使得GCD(e,φ(n))=1且1

计算:

d=e-1Modφ(n)

(3)

其中，d为e的关于模φ(n)的乘法逆元,满足ed=1Modφ(n)。

公钥为(e,n)，私钥为(d,n)。

步骤2：加密信息。

发送者通过式(4)来加密信息M。

C=MeMod(n)

(4)

其中，C是加密后产生的密文。

步骤3：解密信息。

接收者通过式(5)来解密密文C。

M=CdMod(n)

(5)

其中，M是加密前的信息。

传统RSA算法密钥生成过程时间主要是求取最大公约数的时间及计算公钥和私钥模乘法逆元的时间[5-6]。求取最大公约数采用欧几里得算法，其时间复杂度为O(φ(n)/2)，模乘法逆元的计算方法采用穷举法，时间复杂度为O(φ(n))，因此密钥生成的时间复杂度为O(3φ(n)/2)。加密解密计算的时间主要是模幂运算的时间，即形式为XnMod(m)的函数运算时间，其采用递归法实现，时间复杂度为O(n)。所以传统RSA算法密钥生成的时间复杂度为O(φ(n)/2)，加密算法时间复杂度为O(e)，解密算法时间复杂度为O(d)。

在传统的RSA公钥密码体制中一共出现了六个变量：p、q、n、φ(n)、e、d。但是在加密端只能知道n和e，在解密端可以知道p、q、n和d。其中可以将密文解密成明文的密钥是d，即解密密钥。如果d被泄露了，那么加密是无效的。

在加密端，在已知n和e的情况下如何推导出解密密钥d。

由式(3)知，推导d需要知道公钥e和φ(n)。

由式(2)知，只有知道p和q，才能算出φ(n)。

由式(1)知，要想知道p和q，必须对n进行大整数的因子分解。

所以在RSA密码体制中，如果模n被因子分解，那么其私钥d也会被泄露出去[7-9]。虽然至今还未能在理论和事件中证明有分解大整数的有效办法，但大数因子分解未被证明是NP问题，且随着计算机计算能力的提高，原来被认为不可能分解的某些大整数可能会被成功分解，这对RSA密码体制的安全性构成了潜在的威胁[10]。

为了确保RSA加密算法的安全性，只有不断地增加密钥长度。目前，一般要求密钥长度在2 014bit位到2 048bit位之间，甚至更高。

2 RSA算法的改进

改进的RSA算法引进了对三个素数因子的RSA加密算法[11-12]和两个以上的步骤来消除密钥中的n。引进的三个素数因子虽然增加了素数因子的个数，但是减少了素数因子的位数，消除密钥中的n可以使攻击者无法通过因式分解n分解得到因子p和q。所以，一定程度上使得RSA算法更加安全。算法包括三个部分：产生内部密钥(n已经被消除)、加密信息和解密信息。

步骤1：产生密钥。

选择大素数a1、a2、a3，a1≠a2≠a3。计算乘积：

n=a1×a2×a3

(6)

得到欧拉函数：

φ(n)=(a1-1)×(a2-1)×(a3-1)

(7)

根据a1、a2、a3的大小关系，计算X来替代n：

如果a1>a2>a3或者a1>a3>a2，解出X得：

GCD(X,n)=1,n-a1

(8)

如果a2>a1>a3或者a2>a3>a1，解出X得：

GCD(X,n)=1,n-a2

(9)

如果a3>a1>a2或者a3>a2>a1，解出X得：

GCD(X,n)=1,n-a3

(10)

将求得的X代入式(11)，求解出k2：

(11)

现在，公钥是(k1,X)，私钥是(k2,X)。

步骤2：加密信息。

发送者通过公钥(k1,X)来加密信息M，公式为：

C=Mk1Mod(X)

(12)

其中，C是加密后产生的密文。

步骤3：解密信息。

接收者通过私钥(k2,X)来解密密文C，公式为：

(13)

其中，M是加密前的信息。

根据上述步骤，可以设计出改进RSA算法密钥生成的流程，见图1。

通过用X替换n成功消除了n。这让算法变得相对安全，因为攻击者无法通过X分解到a1、a2和a3。

RSA算法的约束是，加密时所取的信息值必须小于大数的值，即小于n的值[13]。

图1 改进RSA密钥生成算法流程图

再者，能够通过另外一层的加密扩展该算法，但是这种大于一层的加密只能运用于二因子的RSA算法，并不适用于三因子的RSA算法。这个可以在计算完X通过重复改进算法中的式(8)～(10)并且得到k2来实现。

但是这一次需要采用获取答案的四次方根。这个方法可以应用更多次，只要取得的值满足所有的约束。

改进的RSA算法密钥生成以及加解密算法所采用的方法是一样的，但是步骤上有所不同。密钥生成算法增加了根据a1、a2、a3的大小替换n的X的计算，时间复杂度为O(2φ(n))，加密算法的时间复杂度为O(k1)；解密算法在模幂运算结果的基础上增加了平方根运算，因为平方根运算的时间复杂度为常数阶，因此解密算法的时间复杂度为O(k2)。

3 实验结果与分析

以计算φ(n)的攻击方法为例，如果在传统的RSA加密算法中，攻击者可以计算出来φ(n)，就能够分解出n的素数因子。这是由于φ(n)=(p-1)(q-1)=pq-(p+q)+1=n-(p+q)+1→p+q=n+1-φ(n)且pq=n，那么可以构造一元二次方程x2-(n+1-φ(n))x+n=0，方程的根就是p和q[14-15]。

例如：如果n=221，φ(n)=192，那么，一元二次方程x2-30x+221=0的两个根为x1=13，x2=17。因此，n=13×17=221。

改进的RSA算法中，在已知公钥的前提下，无法知道公钥中的n，因此无法通过方程分解出n的因子；再者，采用三个素数因子的RSA算法，就算攻击者知道了φ(n)，但是对于分解n的三个素数因子没有一个具体的公式去求解，所以分解的困难度会大大增加，提高了算法的安全性。

表1和表2分别为RSA算法和改进RSA算法在时间上的差异。以滴答(1ms等于10 000滴答)为单位，并只用单层加密，即使用X作为系数。因为此算法专注于RSA算法的安全方面，密钥的生成以及加解密方面增加了计算量，所以时间会有一些增加。

表1 RSA算法的时间

表2 改进RSA算法的时间

图2是RSA算法和改进RSA算法之间产生密钥的时间对比，以滴答为单位。

密钥的产生过程在时间上有很多的变化，因为多余的一些加密步骤或消除n的分布消耗了时间。

图3为RSA算法和改进RSA算法之间加密和解密的时间对比，以滴答为单位。

图2RSA算法和改进RSA算法之间

图3RSA算法和改进RSA算法之间

信息的加密和解密存在时间上的差异，因为解密算法发生了改变。后者更加复杂并会消耗更多时间。

图4为RSA算法和改进RSA算法之间的总体时间对比，以滴答为单位。

图4 RSA算法和改进RSA算法之间的总时间对比

根据上述对传统的RSA算法和改进算法的时间复杂度的分析，两种算法的时间复杂度级别相同，又因为增加的时间并不影响密钥生成以及加解密的过程，消耗的时间并不是很高，因此可以忍受。

4 结束语

由于改进RSA算法克服了传统RSA算法因素数选择问题位数要求越来越多使得素数产生效率下降、n被因子分解密码体制安全性下降等缺点[16]，所以，改进RSA算法具有独特的优势，实现了对信息的安全加密。由于在最初的RSA算法中加入三个素数因子并且消除n，用来替代n最新生成的数不仅可以在公钥和私钥中使用，而且还能成功避免受到因子分解的攻击，使得RSA算法更加安全，但是在时间上会有一些增加，因此还需要对密钥生成、信息的加解密速度和时间进行深入研究。

[1]DiffieW,HellmanME.Newdirectionsincryptography[J].IEEETransactionsonInformationTheory,1976,22(6):644-654.

[2] 胡 云.RSA算法研究与实现[D].北京:北京邮电大学,2010.

[3]AboudSJ.AnefficientmethodforattackRSAscheme[C]//Procofsecondinternationalconferenceonapplicationsofdigitalinformationandwebtechnologies.[s.l.]:IEEE,2009:587-591.

[4]MehrotraV.AneffectivemethodforattackRSAstrategy[J].InternationalJournalonAdvancedNetworkingandApplications,2012,3(5):1362-1366.

[5]RSALaboratory.RSAalgorithmtimecomplexity[EB/OL].2009.http://www.rsa.com/rsalabs/node.aspid=2215.

[6] 靳丽君.非对称加密体制中RSA算法的研究[J].电子设计工程,2011,19(11):29-30.

[7] 李 青,李雄伟,金 涛.RSA算法的研究与简单实现[J].网络安全技术与应用,2007(6):88-91.

[8]JonssonJ,KaliskiB.Thepublic-keycryptographystandards[J].RSADataSecurity,1993,8(5):33-35.

[9]AmbedkarBR,GuptaA,GautamP,etal.AnefficientmethodtofactorizetheRSApublickeyencryption[C]//Procofinternationalconferenceoncommunicationsystemsandnetworktechnologies.[s.l.]:[s.n.],2011.

[10] 鄢喜爱,杨金民,田 华.RSA公钥密码算法的分析[J].长春工业大学学报:自然科学版,2006,27(2):142-144.

[11] 安吉旺,徐凯宏.基于RSA和密钥的二维码加密编码的研究[J].森林工程，2014，30(2):125-129.

[12] 谢仁康.非对称加密二维码防伪系统的设计[D].成都:电子科技大学,2013.

[13]MilanovE.TheRSAalgorithm,UniversityofWashington:DepartmentofMathematics[EB/OL].2013-10-08.http://www.math.washington.edu/～morrow/336_09/papers/Yevgeny.pdf.

[14]DhakarRS,GuptaAK,SharmaP.ModifiedRSAEncryptionAlgorithm(MREA)[C]//ProcofACCT.[s.l.]:[s.n.],2012.

[15]SarkarS,MaitraS.CryptanalysisofRSAwithtwodecryptionexponents[J].InformationProcessingLetters,2010,110(5):178-181.

[16] 刘项洋.基于RSA的随机密钥交换系统的研究与设计[D].合肥:合肥工业大学,2004.

Research and Improvement of RSA Algorithm

CHEN Chun-ling,QI Nian-qiang,YU Han

(College of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

In order to improve the security of the RSA algorithm and avoid the mathematical factorization of the moduleninRSAcrytosystemwhichleadstoprivatekeydleaking,themethodofeliminatingthedistributionofnandthree-factorencryptionalgorithmareadopted.Theresultsshowthattheformercansuccessfullyavoidtheappearanceofninpublickeyandprivatekey,preventingtheattacterfromusingthemethodofmathematicalfactorizationtogetthenfactorsanddeducingthedecryptionkeyd.Adoptingthelatter,eveniftheattackerknowstheφ(n),butitdoesn’thaveaspecificformulatobreakdownthethreeprimenumberfordecompositionofn.Sothedifficultyoffactoringincreasesandthecomputationisreducedduetothereductionoflargeprimenumbers’sbits.TheexperimentalresultsindicatethatthemethodincreasesthesecurityoftheRSAalgorithmanditstimecomplexityissametothetraditionalalgorithm.

RSA;security;public key;private key;time

2015-11-23

2016-03-04

时间：2016-08-01

国家自然科学基金资助项目(11501302)

陈春玲(1961-)，男，教授，硕士，研究生导师，研究方向为软件工程、分布式组件技术、网络信息安全及其应用；齐年强(1991-)，男，硕士研究生，研究方向为网络安全。

http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0904.026.html

TP

A

1673-629X(2016)08-0048-04

10.3969/j.issn.1673-629X.2016.08.010