常庆龙,严谦泰

(1.江苏省泰兴教师进修学校，江苏 泰兴 225400;2.安阳师范学院 数学与统计学院，河南 安阳 455000)



论偶优美图与偶强协调图

常庆龙1,严谦泰2

(1.江苏省泰兴教师进修学校，江苏 泰兴 225400;2.安阳师范学院 数学与统计学院，河南 安阳 455000)

给出了连通图为偶优美图和偶强协调图的充要条件，并对不连通的偶优美性和偶强协调性进行了一些探讨.

优美图；强协调图；偶优美图；偶强协调图

1 引言

1972年，Golomb明确给出了优美图的定义[1].1991年，Gnanajothi定义了奇优美图，并提出猜想：所有的树都是奇优美的[2].1982年，FrankHsu引入了强协调图的概念[3].在此基础上，2003年，王卫军，严谦泰又给出了奇强协调图的概念[4].循此思路，2014年，吴跃生等也提出了偶优美图和偶强协调图的概念[5].目前，国内关于偶优美图和偶强协调图的研究尚属于空白.本文给出一些初步结果，以期抛砖引玉.

本文涉及的图均指有限、无向、简单图，通常用G表示一个图，用V(G)、E(G)、|V(G)|、|E(G)|分别表示图G的顶点集、边集、顶点数、边数.并把有p个顶点q条边的图叫(p,q)图.

定义1[1]对于(p,q)图G，如果存在一个单射(— —映射)

使得对一切uv∈E(G),由θ' (uv)=|θ(u)-θ(v)|导出一个双射(一一对应)

则称θ是G的一个优美标号(或优美值)，称G为优美图，θ'为G的边标号.

定义2[6]设图G是一个优美图，其优美值为θ.如果存在V(G)的一个划分(X,Y),使E(G)中的每条边的两端均分属于X和Y，且满足：

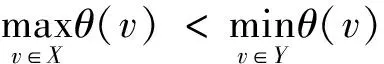
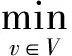
定义3[5]对于(p,q)图G，如果存在一个单射

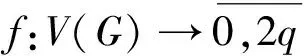
使得对一切uv∈E(G),由f' (uv)=|f(u)-f(v)| 导出一个双射

则称f为G的一个偶优美标号，称G为偶优美图.

定义4[3]对于(p,q)图G，如果存在一个单射

使得对一切uv∈E(G),由φ' (uv)=φ(u)+φ(v) 导出一个双射

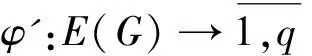
则称φ为G的一个强协调标号，称G为强协调图.

定义5[5]对于(p,q)图G，如果存在一个单射

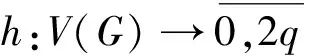
则称h为G的一个偶强协调标号，称G为偶强协调图.

2 主要结果

定理1 任何优美图都是偶优美图.

证 设G是优美图，θ是其优美标号，令f(v)=2θ(v),v∈V(G)，易知f即为G的偶优美标号.

定理2 连通图G为偶优美图的充要条件是G为优美图.

证 由定理1即知充分性成立.

设G为偶优美图且是连通的，易知G的偶优美值均为偶数，只须将所有顶点的偶优美值取其半，即得G的优美值，必要性得证.

定理3 任一优美图与交错图的不交并是偶优美图.

证 设G1为优美图，其优美标号为θ，|E(G)|=q1.G2为交错图，其交错标号为h，|E(G)|=q2，X、Y分别为其小号点集和大号点集.

定义图G1∪G2的顶点标号：

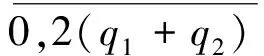
另一方面，由于

{f' (uv)|uv∈E(G2)}

={2(h(u)-h(v) )

+2q1|uv∈E(G2),v∈X,u∈Y}

所以

{f' (uv)|uv∈E(G1∪G2) }

因此

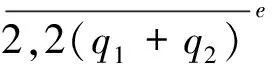
的双射.

综上，f是E(G1∪G2)的偶优美标号，即G1∪G2是偶优美图.

定理4 任何强协调图均为偶强协调图.

证 (显然).

定理5 连通图为偶强协调图的充要条件是其为强协调图.

证 (显然).

定理6 设(p,q)图G为交错图，交错数位m，则当n≥m时，图G∪St(n)为偶强协调图.

证 设G的交错标号为θ，|E(G) |=q，V(St(n))={x0,x1,x2,…xn}，定义图G∪St(n)的顶点标号f如下：

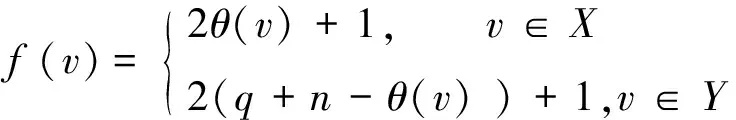
另一方面，由于

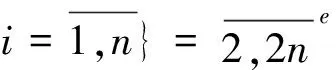
{f' (uv)│uv∈E(G),v∈X,u∈Y}

={2[q+n-(θ(u)-θ(v) ) ]

+2│uv∈E(G),v∈X,u∈Y}

所以，

f' (E(G∪St(n) ) )

由此可知f是G∪St(n)的偶强协调标号.

定理7 设G是强协调图，则并图G∪St(n)(n∈N+)是偶强协调图.

证 设V(St(n) )={x0,x1,x2,…xn}，|E(G) |=q，G的强协调标号为θ.

若n≡1(mod2)，则定义G∪St(n)的顶点标号f如下：

f(v)=2θ(v)+n,v∈V(G)

若n≡0(mod2)，则定义f如下：

f(v)=2θ(v)+n-1,v∈V(G)

容易验证f是G∪St(n)的偶强协调标号.

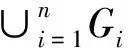
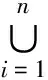
[1]S.W.Golomb.HowtonumberaGraphtheoryandcomputing.AcademicPrees,NewYork(1972),23-37.

[2]R.B.Gnanajothi.Topicsingraphtheory[D].Madurai:MaduraiKamarajUniversity,1991.

[3]FrankHsu.D.HarmoniousLabelingofWindmillgraph,JournalofGraphTheory. 1982,6(1),85-87.

[4]王卫军，严谦泰. 关于图D_(m,4)的奇优美性和奇强协调性[J]. 南阳师范学院学报(自然科学版)，2003,2(9):1-2.

[5]吴跃生，王广富，徐保根. 交错图的奇优美性和协调性. 武汉大学学报(理学版),2014,12(24):10-12.

[6]杨显文. 关于C_(4,m)的优美性[J]. 工程数学学报，1995(4)：108-112.

[责任编辑：张怀涛]

Study on Even Graceful and Even Strongly Harmonious Graphs

CHANG Qing-long1, YAN Qian-tai2

(1.Taixing Teacher’s Sraining School, Taixing 225400，China；2.School of Mathematics and Statistics, Anyang Normal University, Anyang 455000，China)

This paper gaves a necessary and sufficient condition of even graceful and even strongly harmonious graph for connected graphs. Even gracefulness and even strongly harmoniousness are studied for nonconnected graphs.

Graceful graphs; Strongly harmonious graph; Even graceful graph; Even strongly harmonious graph

2016-04-06

河南省自然科学基金(0511013800)；河南省教育厅自然科学基金(12A11003)

常庆龙，男，高级教师，主要研究组合排序与图论;严谦泰(1964-),男，湖北武汉人，教授，主要从事图论及其应用研究。

O

A

1671-5330(2016)05-0059-03