余云彩

（湖北师范大学数学与统计学院，湖北黄石 435002）

稳健方法在线性回归模型中的应用

余云彩

（湖北师范大学数学与统计学院，湖北黄石 435002）

从影响函数和崩溃点角度分析了线性回归模型中最小二乘估计的不稳健性，进而引出M估计这类稳健估计，从理论上分析稳健估计的抗差性，并用R软件对实际数据进行实证研究．结果表明，在处理含有异常点的数据过程中，稳健估计优于最小二乘估计．

线性回归模；M估计；稳健性

0 引言

考虑线性回归模型：

写成向量形式为：

其中，Y＝（Y1，…，Yn）T是n×1的观测向量，β＝（β1，…，βn）T是p×1未知参数向量，e＝（e1，…，en）T是n×1误差向量．

为估计向量β，最常用的方法是最小二乘法，即

其中x＇i＝（x1i，x2i…，xni）．在X满秩的条件下求得β的最小二乘估计：

最小二乘估计虽然有许多优良性质，如在Gauss－Markov假设下，最小二乘估计βLS具有很好的渐近效率，并且βLS是β估计的最佳线性无偏估计（简称BLUE），这一事实奠定了它在线性回归估计中的重要地位．然而它并不是一个稳健的估计，下面我们将从估计量稳健性的两个基本指标影响函数和崩溃点来说明βLS的不稳健性．

假设样本X1，…，Xn独立同分布，X1～H（x），样本协方差阵正定且有界，误差e1，…，en，独立同分布，e1～F（x）．

在模型（1）下，（x1，y1），（x2，y2），…（xn，yn）独立同分布，其联合分布为：

最小二乘估计βLS的统计泛函（记为βLS）是下列方程的解

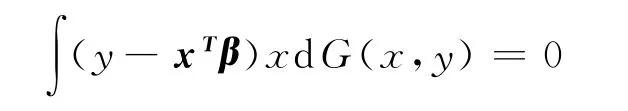
它的影响函数为：

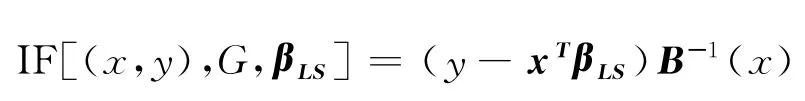
其中B＝∫xxTd H（x）是正定矩阵．显然βLS的影响函数无界，无论是响应变量y还是x的观测数据受到污染，都可能对βLS的估计有很大的影响，并且βLS的渐近崩溃点为：

1 稳健方法

一个非常稳健的估计应该具有受限制的影响和高崩溃点，显然最小二乘估计表现出非常不稳健的特性．为克服这一缺点，我们引入稳健统计中一类常用的M估计．

设X1，…，Xn是来自某总体的一个样本，ρ（x；θ）为非负函数，若θ ＝θ （X）满足

M估计包括很多估计方法，如那些分类为M估计，GM估计，S估计及MM估计的方法，它们都是将最大似然的思想推广用于尺度和位置的稳健测度（Huber［1］）M估计的性质取决于选取的ρ（·），或者与之等价的ψ．如果选取ρ（x；θ）＝－logf（y；θ），得到的是普通最大似然估计．如果ψ无界，渐近崩溃点则为0．为了产生一个能抵抗特异值干扰的估计，我们应该对分布尾部靠外的观察值给予较小的权重，如Huber估计，双权数估计．

Huber估计由Huber函数决定：

对（4）式求导，得到影响函数：

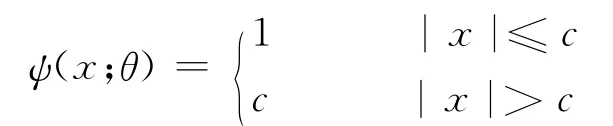
其中c是一个常数，由上述Huber权重的函数可以看出M估计非常稳健，并且与其他用于大样本的稳健测量相比，M估计具有较高的渐进效率，并且随着样本量的增大而具有更高的效率（参考Hogg［2］）．下面我们将定义线性回归模型中的M估计：

其中Q（β）为目标函数，β＝（β1，β2，…，βp）是p维向量．

将目标函数Q（β）限定为带有非降的导数ψ（·），即ρ为凸函数，则（5）可等价地写成

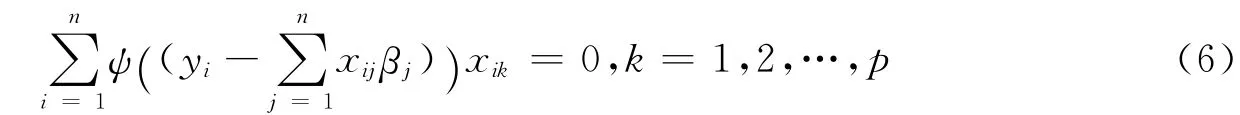
回归的M估计是位置M估计的一种扩展，从形式上看，它是将残差的某种函数进行最小化，其稳健性也取决于函数ρ和ψ的选择．

求解回归M估计的过程是一个复杂过程，因为残差在模型未建立起来之前是一个未知量，而估计结果在残差未知的情况下也无法直接求出来，所以必须用迭代程序．主要做法是开始给一个好的初始估计β（0），然后在式（5）中应用一步牛顿法，一般地，把最小二乘估计作为初始估计β（0）（尽管最小二乘估计具有比较差的稳健性质）．

M估计对重尾误差和不定误差具有很好的耐抗性，通常也有很高的渐近效率和崩溃点，然而它不能处理杠杆效应，对异常变化的随机量X没有很好的抵抗性．通常情况下可以用改进的M估计，利用M－S算法得到MM估计来处理杠杆效应，详细过程可参考Rousseeuw［3］．

2 实际应用

下列是来源于Rousseeuw［3］（p．27，table 3）的天鹅座方向郝－罗素图数据，变量log．Te表示的是恒星表面的实际温度（取对数），变量log．light表示的是光密度（取对数）．

表1 天鹅座方向郝－罗素图数据

考察星座光密度与星座表面的实际温度的关系，可以模拟一元线性回归模型：

用最小二乘法得到回归直线：

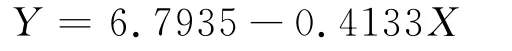
我们将这条直线与星座光密度对星座表面的实际温度的散点图共同绘制在图1中．

图1 光密度对星座表面的实际温度的散点图和拟合的最小二乘回归直线

从散点图看，光密度与星座表面的实际温度应该是正相关，而我们拟合的最小二乘回归线的斜率为负，意味着负相关，与实际情况不同．从图1可以发现，回归线被拉向第11，20，30，34这4个点，说明这四个点严重影响了我们建立的回归模型，我们称这4个点为异常点，也可以叫杠杆效应点．为了处理异常点，下面采取稳健的方法来模拟模型（7）．

1）用M估计（用Huber函数）得到稳健回归直线：

2）用MM估计得到稳健回归直线：

为了方便比较，我们把散点图和所有模拟的回归直线共同绘制在图2中．

图2 光密度对星座表面的实际温度的散点图和拟合的最小二乘和稳健回归直线

图2表明，M估计（Huber函数）虽然降低了异常点的权重，但是斜率仍然是负值，甚至其模拟结果比最小二乘还要差，可见Huber估计还是会受杠杆效应的影响，而改进后的MM估计能很好地抵抗异常的干扰．

参考文献：

［1］Yohai V J．Robust estimation in the linear model［J］．Ann Statist，1974，2：562～567．

［2］Hogg R V．Adaptive robust procedures［J］．Amer Statist Associ，1974，69：909～927．

［3］Rousseeuw P J，Leroy A M．Robust regression and outlier detection［M］．New York：Wiley，1987．

［4］陈希孺，赵林城．线性模型中的M方法［M］．上海：上海科学技术出版社，1996．

［5］Huber P J．Robust statistics［M］．New York：Wiley，1981．

［6］Yohai V J，Maronna R A．Asymptotic behavior of M－estimates for the linear model［J］．Ann Statist，1979，7：258 ～268．

［7］Zhao L C．Strong consistency of M－estimates in linear models［J］．Sci China Ser A，2002，45：1420～1427．

［8］Wu L，Qiu J．Applied multivariate statistical analysis and related topics with R［M］．Beijing：Science Press，2013．

［9］Chatterjee S，Hadi A S．Regression analysis by example，5th edn［M］．Beijing：China Machine Press，2013．

［10］Yohai V J．High Breakdown－Point and high efficiency robust estimates for regression［J］．Ann Statist，1987，15：642～656．

［11］Chatterjee S，Price B．Regression analysis by example［M］．New York：Wiley，1977．

Robust methods applied in linear regression models

YU Yun－cai

（College of Mathematics and Statistics，Hubei Normal University，Huangshi 435002，China）

This paper considers some estimators in linear regression model，least－squares estimator is Confirmed the lack of robustness by analyzing their influence function and breakdown point，robust estimators such as M－estimator is investigated．In addition，the resistant of the robust estimators are analyzed theoretically and empirical application to the actual data by R software illustrates that robust estimators are significantly superior to least squares estimate when data contain outliers．

linear regression model；M－estimator；robustness

O212．1

A

1009－2714（2016）04－0035－05

10．3969／j．issn．1009－2714．2016．04．009

2016—02—18

余云彩（1990— ），男，湖北阳新人，硕士，研究方向为回归分析．