汪丽仙

（浙江省常山县第一中学）

小构造 大智慧
——例谈“特例法”在解几何问题中的应用

汪丽仙

（浙江省常山县第一中学）

俗话说：“授人以鱼，不如授人以渔.”然而“渔”的方式也是多种多样的，学在平时，但也只为六月试锋，金榜题名.恰逢学校举行了一场教学比武，本人选择的课题是“特例法在解几何问题中的应用”，一是出于所任教的文科班级学生基础薄弱，在提升其知识掌握量及度上较困难时，如何帮助他们多得分的考虑，二是想尝试一下学生对特例法的接受及应用程度，以便在平时的教学中加以渗透和推广.下面就这堂课的一些教学片断展开，谈谈本人的一些想法.

根据平时的教学、作业和测试，选取了学生较惧怕的平面向量运算，并结合平时的教学进行了选题.

问题1：已知正方形ABCD的边长为1，点E是AB边上的动点，则的值为.

学生2：以直线AB、AD分别为x、y轴建立平面直角坐标系，则B（1，0），C（1，1），D（0，1），设E（x，0）

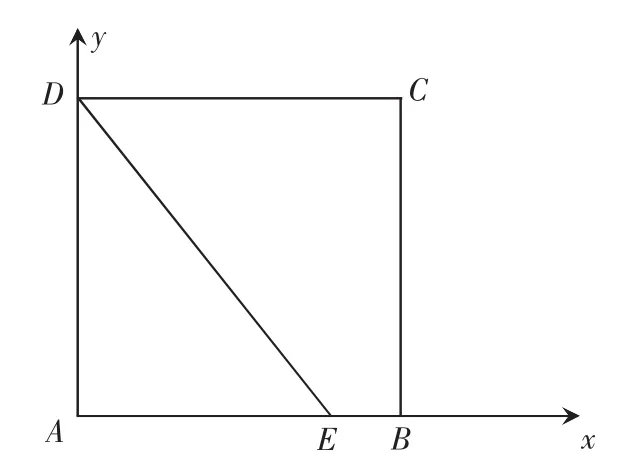
学生3：取E为AB中点，用学生1或学生2的方式求出的结果是一样的.笔者趁机提出“是不是可以将E点取得更为特殊一些呢？”

这时从学生表情上可以明显地感觉到他们心灵的震撼.

问题2：在△ABC中，M是BC的中点，AM=3，BC=10，则·=______ _.

学生5：取△ABC为等腰三角形，则AM⊥BC

以M为坐标原点，直线MC、MA分别为x、y轴

建立平面直角坐标系，则B（-5，0），C（5，0），A（0，3）

学生6：取△ABC为等腰三角形，则AM⊥BC

大多数学生都能想到以上的解法，转化成学生熟悉的三角形计算问题对多数学生来说易接受，这也说明了特例法具有较强的实用性和可操作性.

三角形中的外心、内心、重心、垂心对很多学生来说概念不清、易混淆，这一问题又牵涉了向量，所以成为多数学生口中的难题.但如果从特例入手，却有种“拨开云雾见晴青天”的意境，而事实证明确实如此.此题一给出，不到3分钟便有了回应.

学生10：取△ABC为直角三角形，则O为斜边的中点.若BC为斜边，则，即P与A重合，所以P为△ABC的垂心.

这堂课是在高二学生中开设的，选取的题目基本是高考题，但随着课题的给出，学生处理起来游刃有余，而且积极性高涨，这足以证明特例法易被学生接受和应用.教学比武虽然落下了帷幕，但这一方法一直延续到笔者的课堂里，而且学生受益匪浅.

例1.如下图所示，在平行四边形ABCD中，E为BC的中点，F为CD的四分之一点，设，则m+n=______ _.

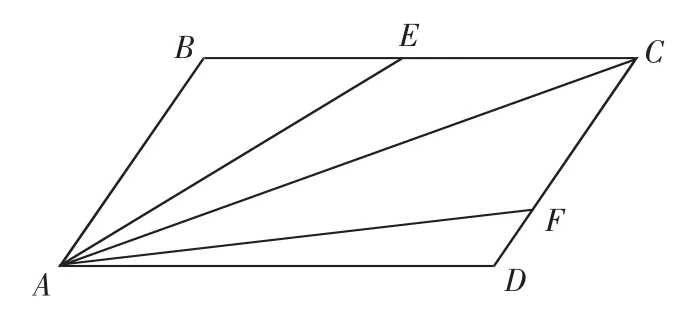
取平行四边形ABCD为正方形，以直线AB、AD分别为x、y轴建立平面直角坐标系，设AB=1，

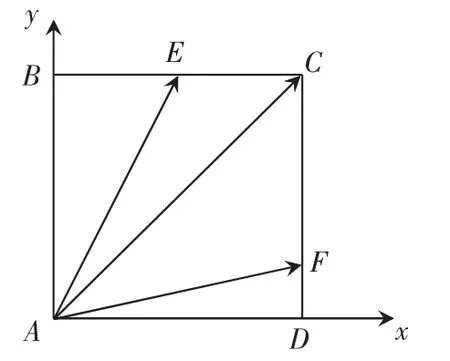
此题错误率极高，原因是学生表示向量时很混乱，这一特例则省去了平面向量的表示，转化成为坐标的运算，思路清晰.

这一特例的处理让学生从复杂的设未知数运算中得到了“解脱”.

例3.如图，在等腰梯形ABCD中，AB∥CD且AB=2AD，设∠DAB=θ，θ∈（0，），以A、B为焦点且过点D的双曲线的离心率为e1，以C、D为焦点且过点A的椭圆的离心率为e2，则e1·e2= _____.

此题题干让较多学生有“晕”的感觉，加之已知量少，所以运算较难进行，这一特例则使运算得以开展.

例4.在三棱锥T-ABC中，TA，TB，TC两两互相垂直，T在底面ABC上的正投影为D，下列命题：

①TA⊥BC，TB⊥AC，TC⊥AB；

②△ABC是锐角三角形；

其中正确的是______.（写出所有正确命题的编号）

在正方体中取三棱锥T-ABC，则易得①②③均正确，④错误.

此类题是大多数学生惧怕的题型，多选怕错，所以很多学生宁可少选，也不多选，通过取特例建立模型既节省了时间又提高了正确率，更重要的是学生克服了恐惧敢于下手去做，提升了自信心.

诸如此类的例子举不胜举，可以说，学生对特例法的接受、理解、应用程度是笔者始料不及的.作为教师，如果我们能多去观察并了解学生的“需求”，“供应”得恰到好处，相信我们离“供需平衡”的目标就更近了一步.

·编辑 孙玲娟