班桂宁，聂婷婷，陈科成

（广西大学 数学与信息科学学院，广西 南宁530004）

群论是数学史上的一座丰碑，从1829年伽罗瓦通过运用群的方法解决方程根式求解的充要条件至今，群论已有了翻天覆地的发展.群论普遍地被认为是数学及其它许多应用中的基本工具.有限p－群与群的自同构［1］是群论的基础.在有限非交换p－群中有一类有限p－群被定义为LA－群，即p－群G的阶能整除其自同构Aut（G）的阶，则｜G｜｜｜Aut（G）｜，｜G｜＞p2.关于LA－群及有限p－群自同构的研究俞曙霞、班桂宁等已取得了大量有价值的成果［2～5］.本文结合Rodney James关于p2－p6阶的分类［6］针对p6阶群的Φ36家族进行群的有效扩张，得到一类新非交换的p－群，然后运用自由群理论证明该群的存在性，并给出该群的一些基本性质，最后利用群的中心内自同构特性证明该群是LA－群.

1 基本引论

公式1［7］设G是群，a，b，c∈G，则有：

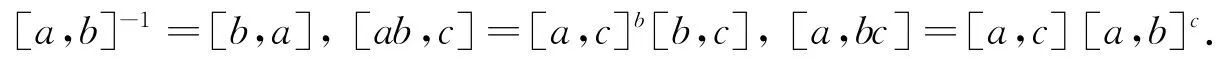
公式2［7］设G是群，a，b∈G且［a，b］∈Z（G），n是正整数，则有：

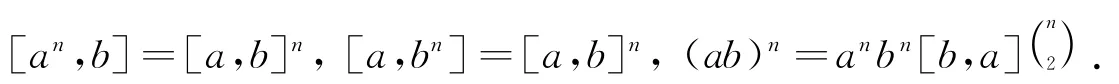
公式3［7］设G是亚交换群，a，b∈G，m≥2，i，j是正整数，则有：

其中：求积符号中的i，j为正整数，且满足i＋j≤m.

引理1［7］设G是有限p－群，若c（G）＜p，则G正则.

引理2［7］设G是有限群，则G的全体中心内自同构组成Aut（G）的子群，且它与Z（G/Z（G））是同构的.

引理3［8］设G是PN群，G/G′和Z（G）的不变型分别为m1≥m2≥… ≥mt≥1和k1≥k2≥…≥ks≥1，则｜Ac（G）｜＝pa，其中a＝∑min｛mj，ki｝.

2 结果

定理1 设

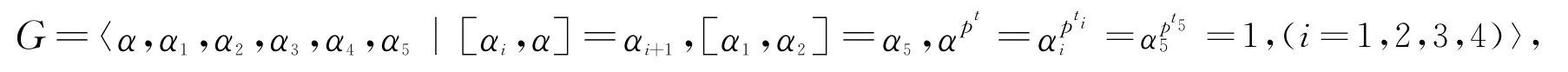
则G构成群的充要条件是：

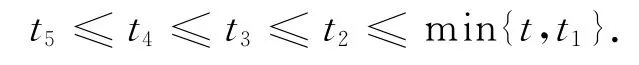
在G成群的条件下，有：

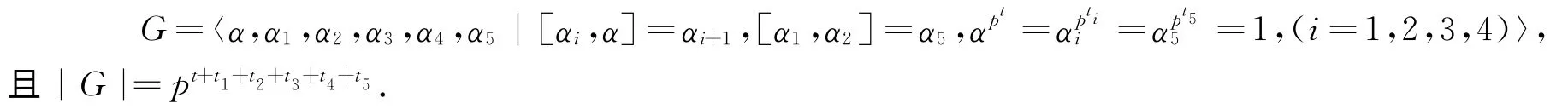
证明（I）假设定理中所给的G是一个群.由［αi，α］＝αi＋1，［α1，α2］＝α5，得：

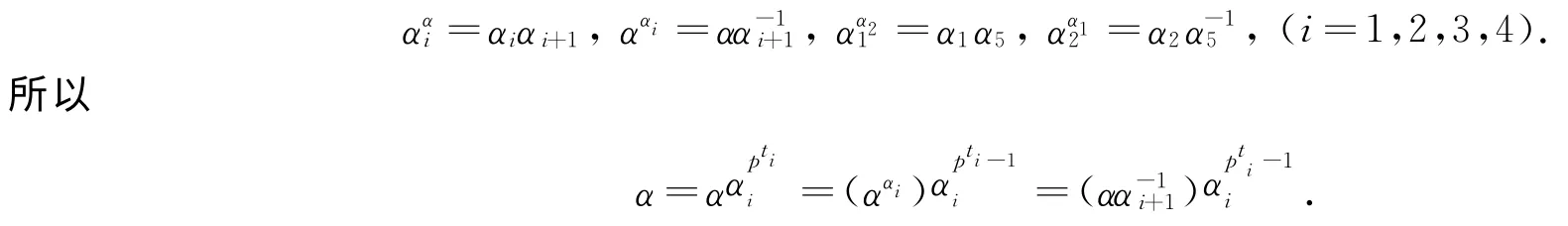
（1）当i＝1时，有：

（2）当i≠1时，有：

综上可得：

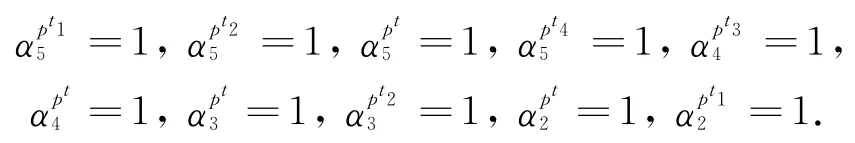
因为

所以

综合上述条件有：

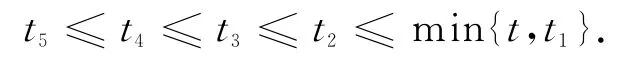
（II）证明G的存在性.

令

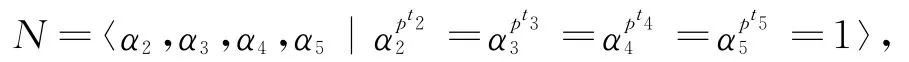
设F＝〈α〉为阶循环群，映射τ如下的作用在N上：

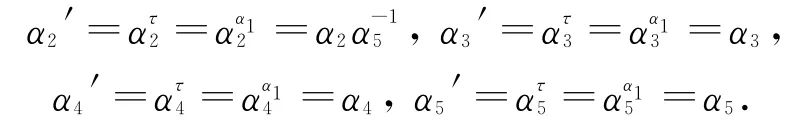
则由t5≤t2，得：

由t5≤t4≤t3≤t2≤t1，得：

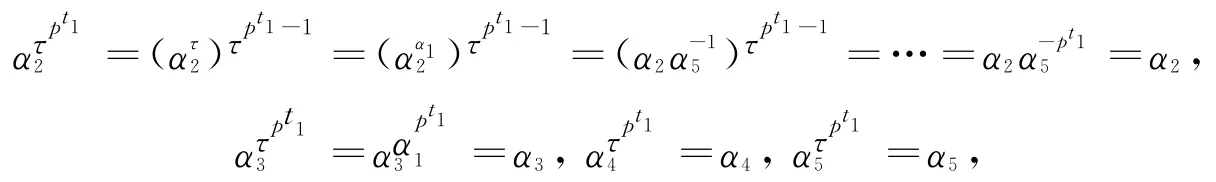
若此时记扩张函数f：F×F→N和α：F→Aut（N）有如下形式：

则由Schreier扩张理论得到N被F的一个扩张.

设在同构σ：F→G1/N下t的像为为陪集中选定的代表元，满足.令，则有：

且

即

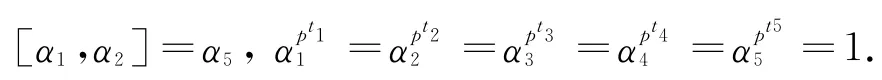
因此G1是存在的，且.

根据自由群理论证明G1即为群G1的定义关系.

设F＝｛x1，x2，x3，x4，x5｝是一个自由群，

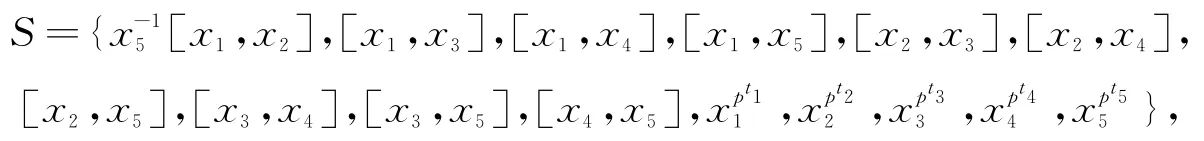
则

因此

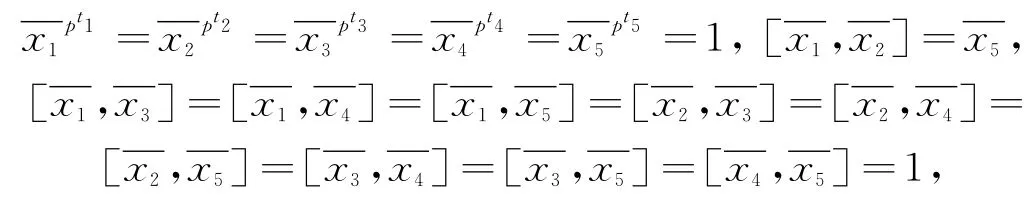
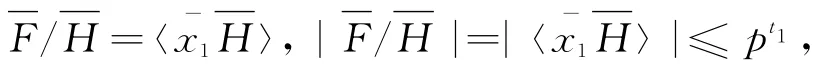
故

所以

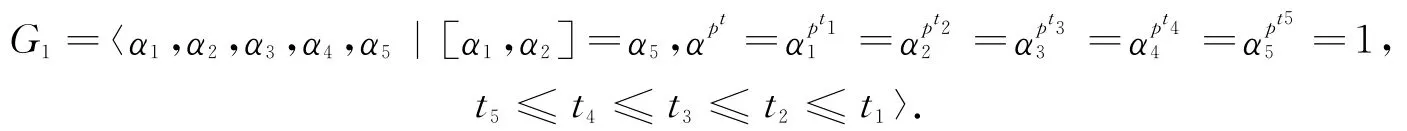
令

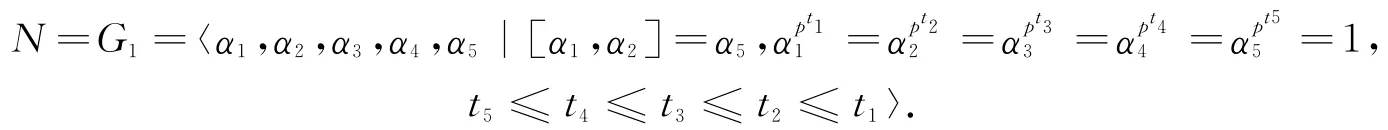
设F＝〈a〉为pt阶循环群，映射τ如下作用在N上：

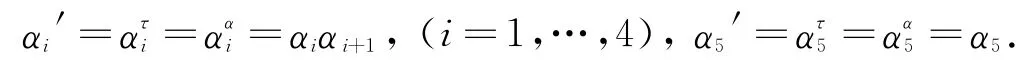
由t5≤t4≤t3≤t2≤t1，得：

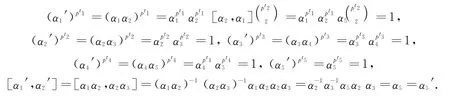
因此有：

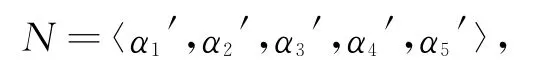
故τ∈Aut（N），显然1τ＝1，下证.

由t5≤t4≤t3≤t2≤min｛t，t1｝，得：

则由Schreier扩张理论得到N被F的一个扩张G＝Ext（N，pt；1，τ）且.

即［αi，α］＝αi＋1.因此G是存在的，且.

根据自由群理论证明G1即为群G1的定义关系.

设F＝｛x，x1，x2，x3，x4，x5｝是一个自由群，

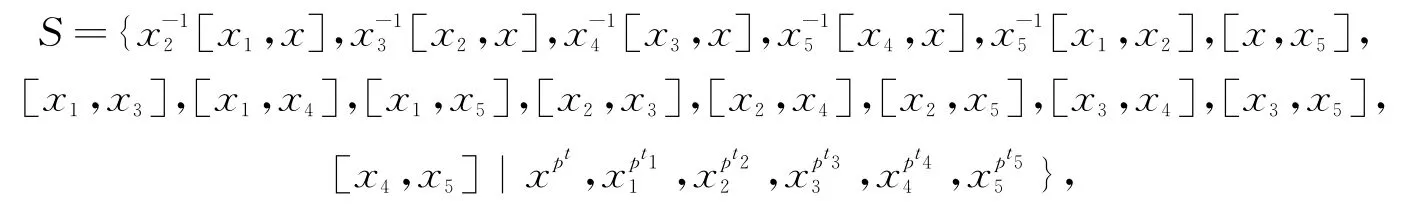
则

因此

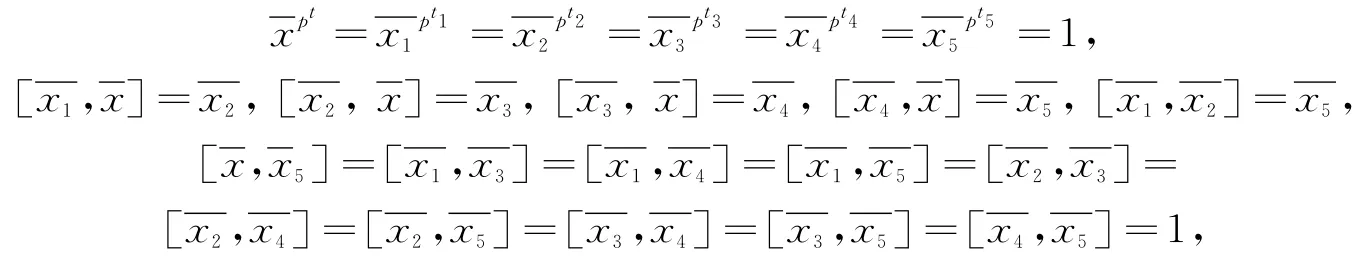
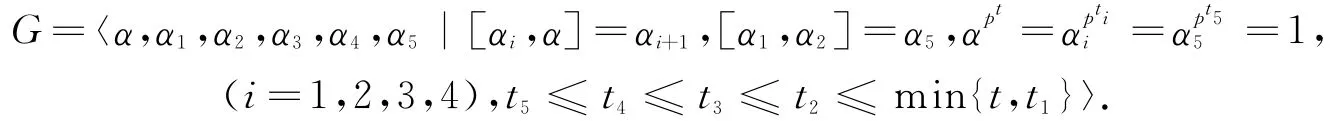
定理2 群G有下列性质：

（1）G′＝G2＝〈α2，α3，α4，α5〉，G3＝〈α3，α4，α5〉，G4＝〈α4，α5〉，G5＝〈α5〉，G/G′＝〈αG′，α1G′〉，P（G）＝〈gp｜g∈G〉，Φ（G）＝〈α2，α3，α4，α5〉〈αp，α1p〉.

（2）G为亚交换p－群.

（3）若p＞5，则G为正则p－群.

（7）若t＝t1＝t2＝t3＝t4＝t5＝1，则.

证明（1） （i）由G的定义关系，显然有〈α2，α3，α4，α5〉≤G′，且〈α2，α3，α4，α5〉◁G′.令N＝〈α2，α3，α4，α5〉，则G/N＝〈αN，α1N〉，因为［α1，α］＝α2∈N，所以［αN，α1N］＝N，故G/N为交换群，可以得到.证明如下：

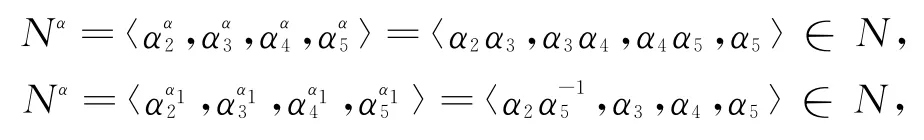
由引理2得G′≤N，即G′＝G2＝〈α2，α3，α4，α5〉，从而可得G/G′＝〈αG′，α1G′〉.

（ii）因为

［α1，α］＝α2，［α2，α］＝α3，［α3，α］＝α4，［α1，α2］＝α5，

从而G3＝［G，G2］＝〈α3，α4，α5〉.

同理G4＝［G，G3］＝〈α4，α5〉；G5＝［G，G4］＝〈α5〉；G6＝1.可得c（G）＝5.

（iii）由有限群G的子群P（G）定义有P（G）＝〈gp｜g∈G〉，即的frattini子群.

（2）因为［α2，α3］＝［α2，α4］＝［α2，α5］＝［α3，α4］＝［α3，α5］＝［α4，α5］＝1，所以G″＝［G′，G′］＝1，故G为亚交换p－群.

（3）当p＞5时，由（1）知c（G）＝5＜p，所以G为正则p－群.

（4）对任意的z∈Z（G），设，则

由此可得：

这使得

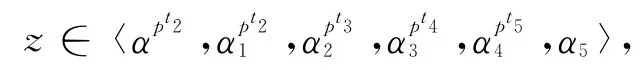
即

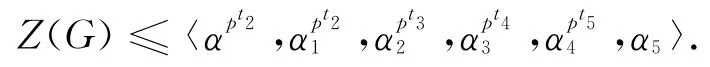
由z的任意性可得，于是

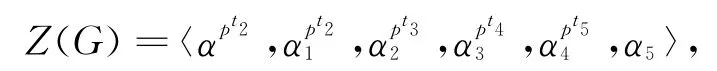
从而

（5）因为Z2（G）/Z1（G）＝Z（G/Z1），所以［Z2（G），G］⊆Z1（G），那么对任意的Z2（G），有：

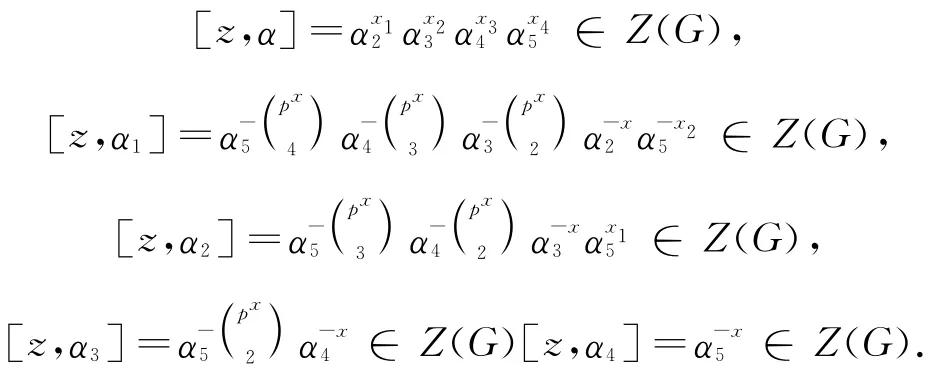
由此可得：

使得

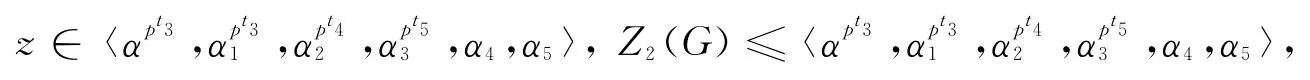
即由z的任意性可得：

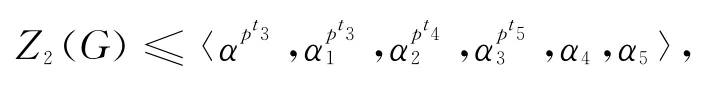
于是：

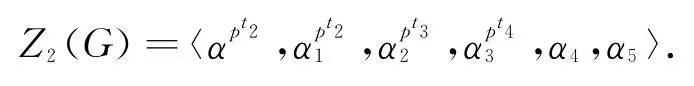
所以

（6）因为Z3（G）/Z2（G）＝Z（G/Z2），且有［Z3（G），G］⊆Z2（G），那么对任意的Z3（G），由（5）得所以

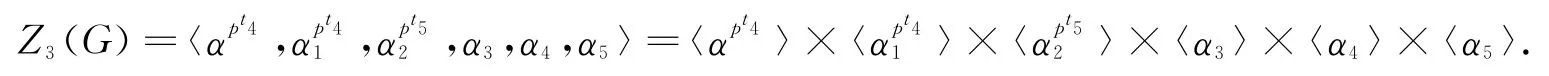
于是

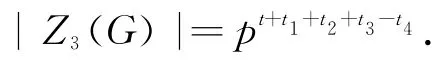
同理

综上可得：

是G的中心群列.

（7）若t＝t1＝t2＝t3＝t4＝t5＝1，则.

定理3 证明新群G为LA－群

证明 令R＝Inn（G）Ac（G）（Ac（G）为G的中心自同构），则易知R为Aut（G）的正规p子群.于是只需证明｜R｜≥｜G｜，即可知G为LA－群.

由引理3得：

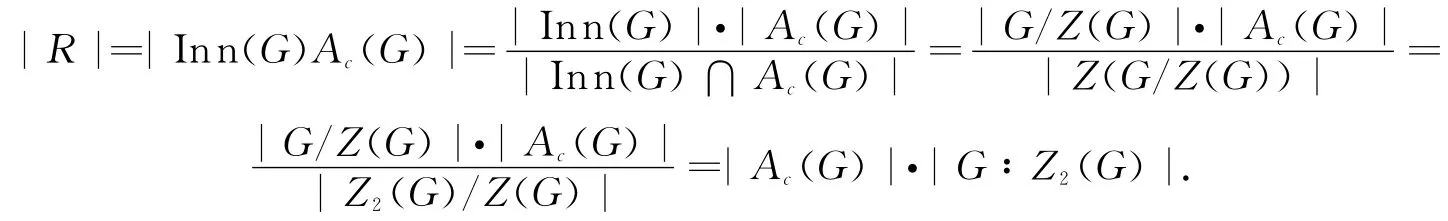
由定理2的（1）知：

其不变型为（t，t1）.

由定理2的（3）知：

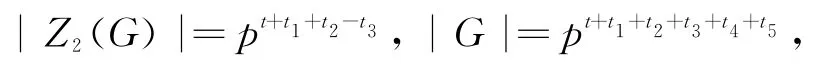
所以

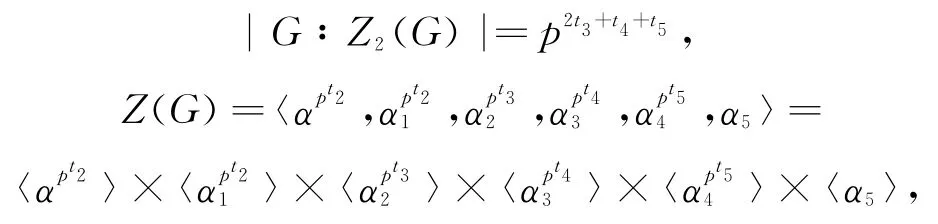
其不变型为：

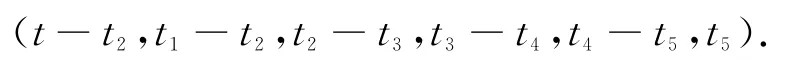
由G/G′的不变型为（t，t1）根据引理3把G分成两组讨论：t≥t1与t≤t1.只要证明这两种情况，即证得G均为LA－群.

（A）证明t≥t1时G为LA－群.

t≥t1时已有t－t2≥t1－t2，t≥t1≥t5成立，Z（G）的不变形为：

下面分析t，t1，t－t2，t1－t2，t2－t3，t3－t4，t4－t5，t5的大小关系.

（I）当t1－t2≥t2－t3时，

（i）t1－t2≥t2－t3≥t3－t4≥t4－t5≥t5时t－t2≥t1－t2≥t2－t3≥t3－t4≥t4－t5≥t5.

计算a时分以下两类：

（1）t1≥t－t2时，

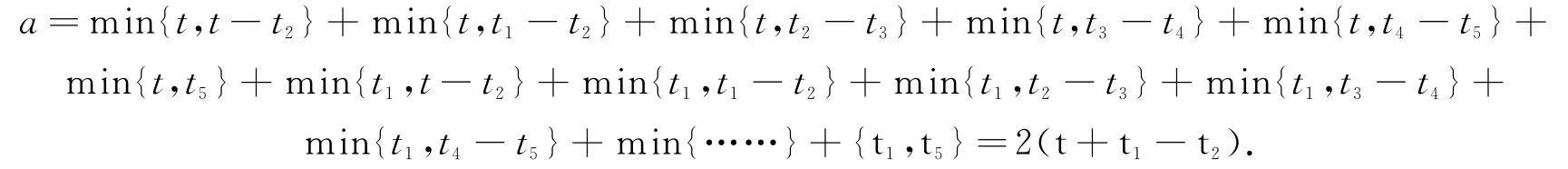
因此

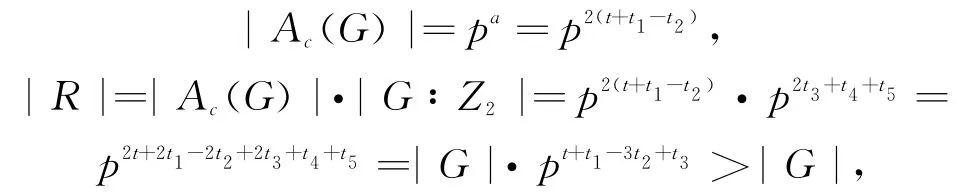
故群G为LA－群.

（2）t－t2≥t1时，a＝t＋3t1－t2，故，故群G为LA－群.

（ii）同理关于t1－t2≥t2－t3时的其它大小关系：

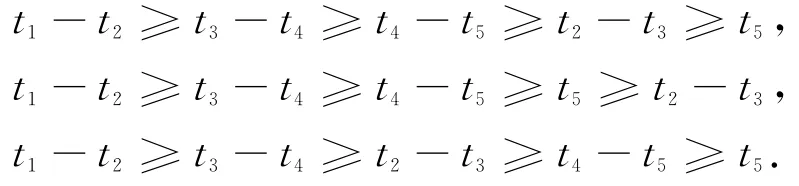
完全可按（i）中的方式验证G是LA－群.

（II）当t－t2≥t2－t3≥t1－t2时，分以下4种情况：

（i）t2－t3≥t1－t2≥t3－t4≥t4－t5≥t5时，t－t2≥t2－t3≥t1－t2≥t3－t4≥t4－t5≥t5.

计算a时分以下3类：

（1）t1≥t－t2时与上述（I）（i）（1）相同，因此G为LA－群.

（2）t－t2≥t1≥t2－t3时，a＝t＋t1＋t2，因此，G为LA－群.

（3）t2－t3≥t1≥t1－t2时，a＝t＋3t1－t2，因此，G为LA－群.

（ii）t2－t3≥t3－t4≥t4－t5≥t1－t2≥t5时，t－t2≥t2－t3≥t3－t4≥t4－t5≥t1－t2≥t5.

计算a时分以下两类：

（1）t4－t5≥t1≥t1－t2时，a＝t＋6t1－2t2＋t5，因此，G为LA－群.

（2）t3－t4≥t1≥t4－t5时，a＝t＋5t1－2t2＋t4，因此，G为LA－群.

（iii）t2－t3≥t3－t4≥t1－t2≥t4－t5≥t5时，t－t2≥t2－t3≥t3－t4≥t1－t2≥t4－t5≥t5.

计算a时分以下两类：

（1）t2－t3≥t1≥t3－t4时，a＝t＋3t1－t2，故，故群G为LA－群.

（2）t3－t4≥t1≥t1－t2时，a＝t＋5t1－2t2＋t4，故，故群G为LA－群.

（iv）t2－t3≥t3－t4≥t4－t5≥t5≥t1－t2时，a＝t＋6t1－2t2＋t5，故G｜，G为LA－群.

（B）证明t≤t1时群G为LA－群.t≥t1与t≤t1是完全相同的讨论方法.同理t≤t1时G为LA－群.

综上可知扩展的群：

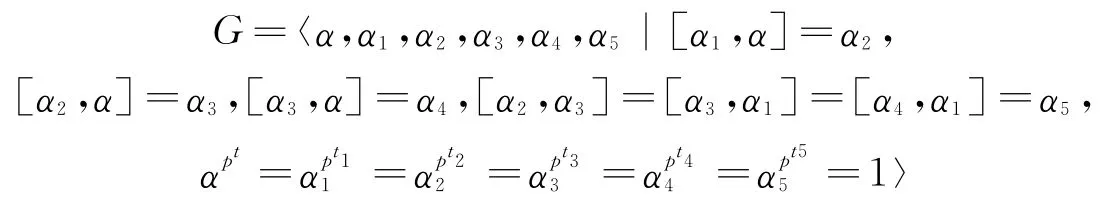
是LA－群.

［1］Flynn J，MacHale D，O’Brien E A，etal.Finite groups whose automorphism groups are 2－groups［J］.Proc Roy Irish Acad Sect A，1944，94（2）：137－145.

［2］Yu S X，Ban G N，Zhang J S.Mininalp－group with automorphism groups of order［J］.Alg Colloq，1966，3（2）：97－106.

［3］俞曙霞，班桂宁.具有循环中心和小中心商的有限p－群［J］.广西大学学报（自然科学版），1993，18（3）：15－23.

［4］Ban G N，Zhang J S，Yu S X.The lower bound for the order of the automorphism groups［J］.Proc Roy Irish Acad.Vol.A，1996，96（2）：159－167.

［5］Ban Guining，Chen Liying，Zhou Yu.A new series of LA－groups［J］.J Guangxi Teachers Education University，2007，24（4）：5－7.

［6］James R.The groups of orderp6（pan odd prime）［J］.Math Comput，1980，34：613－637.

［7］徐明曜.有限群导引（上，下）（第二版）［M］.北京：科学出版社，2001.

［8］Exarchakos T.LA－groups［J］.J Math Soc Japan，1981，33（2）：185－190.