唐永超，王同科

（天津师范大学数学科学学院，天津 300387）

奇异两点边值问题改进的梯形公式外推方法

唐永超，王同科

（天津师范大学数学科学学院，天津 300387）

研究奇异两点边值问题的高精度数值方法.首先，将奇异两点边值问题转化为奇异积分的计算问题.其次，利用改进的复合梯形公式离散奇异积分，针对几种不同情形给出了误差渐近展开式.再次，由误差估计式设计了一种改进的龙贝格算法，利用该算法可以得到问题的高精度数值解.最后，通过数值算例说明了算法的有效性.

奇异两点边值问题；复合梯形积分公式；分数阶泰勒展开式；误差渐近展开；龙贝格算法

1 引言与预备知识

奇异两点边值问题在现代化学、物理及相关学科中具有广泛的应用，其数值算法的研究一直受到重视，该问题的数值算法主要有有限差分方法[1]及其样条求解[2]或外推[3]、Adomian分解方法及改进的ADM方法[4-5]，还有研究利用格林函数将其转化为积分方程，再利用插值离散积分方程进行求解[6-7].本研究考虑奇异两点边值问题，设其源项中不含有未知函数.基本思想是将其转化为奇异积分的计算问题，再利用改进的梯形公式及其外推，得到问题的高精度数值解.

下面简要给出奇异积分梯形公式的误差渐近展开式，详细推导见文献[8].设函数f（x）在除端点x= a、b外充分光滑，考虑如下积分：

设f（x）在x=a和x=b处分别有分数阶泰勒展开式：

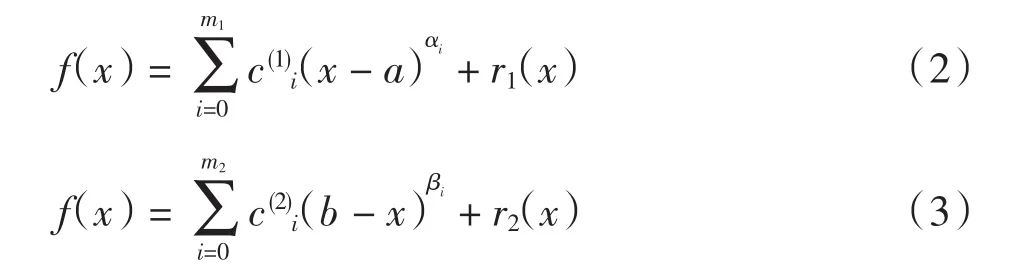
其中：αi、βi为整数或分数，且满足α0＜α1＜…＜αm1和β0＜β1＜…＜βm2；r1（x）和r2（x）充分光滑.这里假定α0＞-1，β0＞-1，以保证积分（1）存在.将区间[a，b]剖分为n等份，步长h=（b-a）/n，节点xi=a+ih，i=0，1，…，n.在区间[a，b]上定义如下改进的梯形公式：

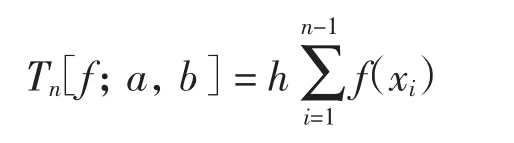
当α0≥0时，

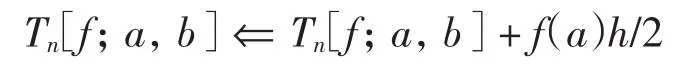
当β0≥0时，

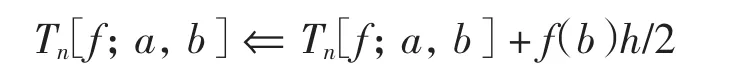
记

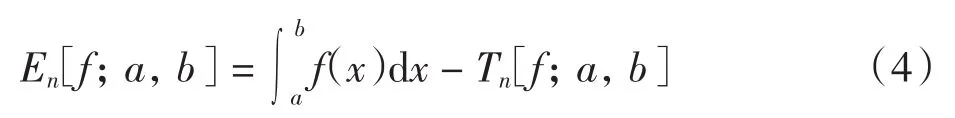
引理1[8]若f（x）在［a，b］上充分光滑，则有

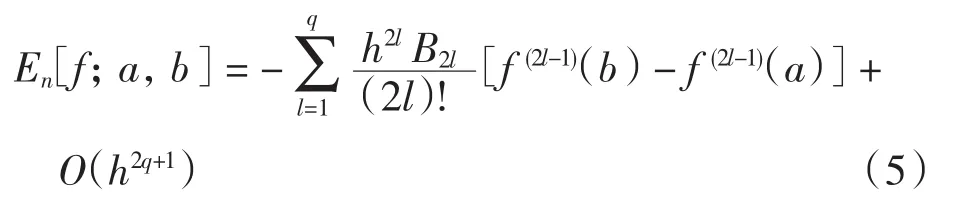
引理2[8]若f（x）在（a，b］上充分光滑，且在x=a处有分数阶泰勒展开式（2），则有

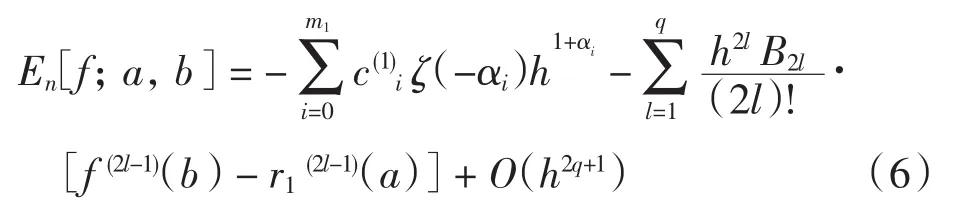
其中：ζ（s）是黎曼zeta函数，当s＞1时，ζ（s）=，并由解析延拓使其当s≠1时有意义；Bk（k=0， 1，2，…）是伯努利数，满足：

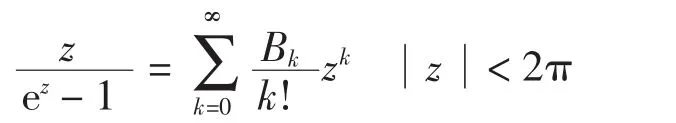
引理3[8]若f（x）在［a，b）上充分光滑，且在x=b处有分数阶泰勒展开式（3），则有

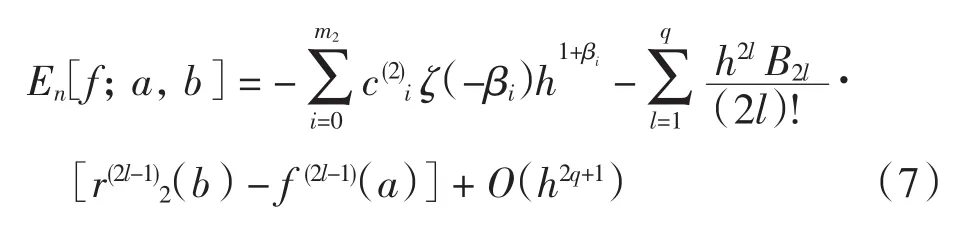
引理4[8]若f（x）在（a，b）上充分光滑，且在x=a和x=b处分别有分数阶泰勒展开式（2）和（3），则有

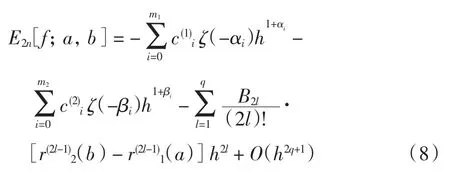
2 计算格式与误差估计

考虑线性奇异两点边值问题：

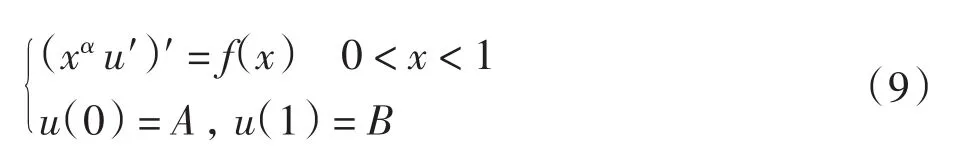
其中：0＜α＜1，f（x）在区间[0，1]上非充分光滑或奇异.

对式（9）在区间[0，1]上直接积分，得到其积分形式的精确解为：

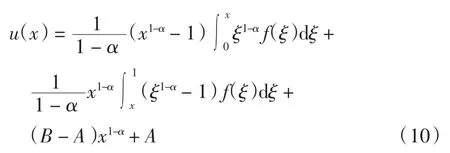
若式（10）右端可以准确求出，则自然得到方程（9）的精确解.但通常情况下，需使用数值积分公式求其在[0，1]区间某点的数值解.下面使用改进的梯形公式和龙贝格外推算法处理.对上述问题考虑以下2种情形：

情形1：f（ξ）仅在ξ=0处分数阶可导，其分数阶泰勒展开式如式（2）所示，则F（ξ）=ξ1-αf（ξ）也在ξ=0处分数阶可导，其分数阶泰勒展开式为

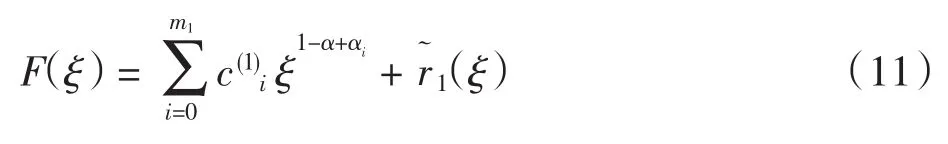
令h=x/n，由引理2有

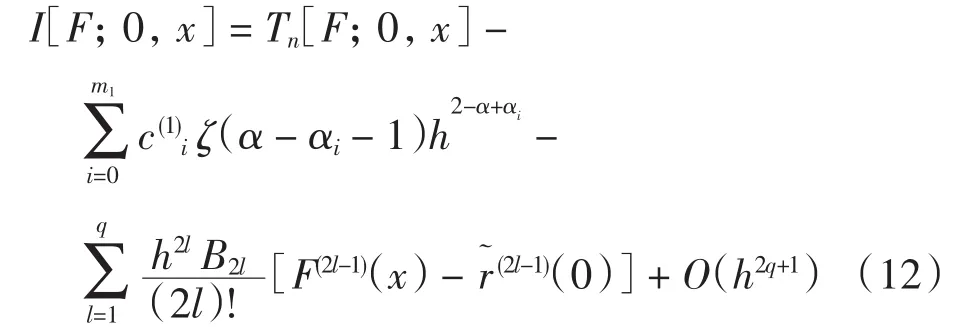
式（10）右端第2个积分为正常积分，令G（ξ）=（ξ1-α-1）f（ξ）及h=（1-x）/n，由引理1有

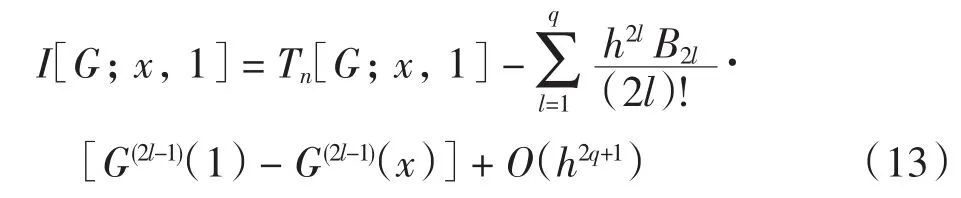
由式（10）、式（12）和式（13），可以得出方程（9）的数值解及误差估计.

情形2：f（ξ）在ξ=0和ξ=a处有分数阶导数，分为2种情形，即0＜a＜x和x＜a＜1.

情形2.1：0＜a＜x.此时，F（ξ）分别在ξ=0和ξ=a处有分数阶导数.F（ξ）在ξ=0处的分数阶泰勒展开式为式（11），F（ξ）在ξ=a处的分数阶泰勒展开式为

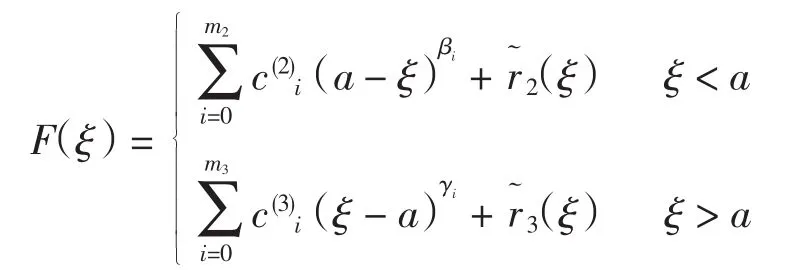
将式（10）的第1个积分分解，得

令h=a/n，由引理4有

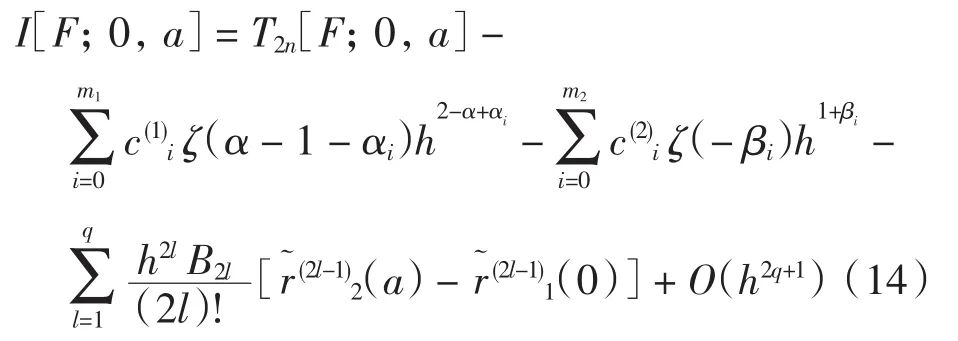
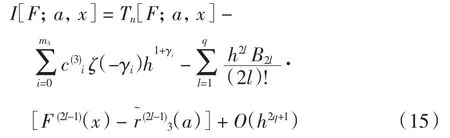
对于正常积分 ，其计算公式及误差估计仍为式（13）.由式（10）、式（13）和式（14），可以得出方程（9）的数值解及误差估计.

情形2.2：x＜a＜1.F（ξ）在ξ=0处的分数阶泰勒展开式仍为式（11）.G（ξ）在ξ=a处的分数阶泰勒展开式为

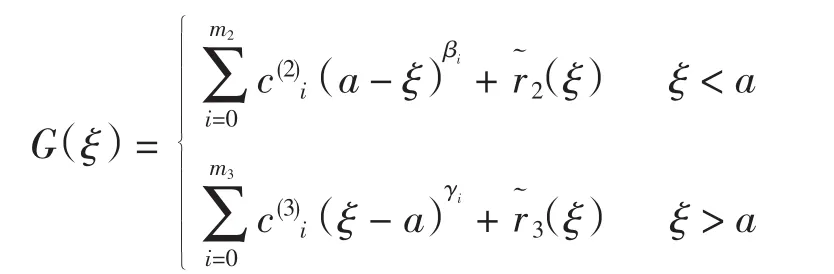
令h=x/n，I［F；0，x］的梯形公式及误差估计式为式（12）.令h=（a-x）/n，由引理3有

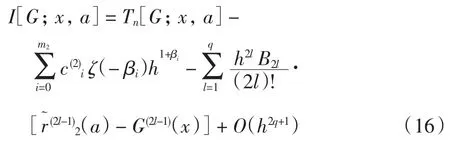
再令h=（1-a）/n，由引理2有

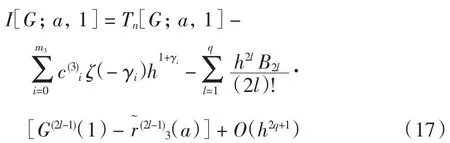
由式（10）、式（12）、式（16）和式（17），可以得出方程（9）的数值解及误差估计.

前面给出3种情形的复合梯形公式的误差估计式，在实际计算时，应对梯形公式进行外推，以消去误差低阶项，提高计算精度.下面给出修正的龙贝格外推算法，以式（14）为例，记

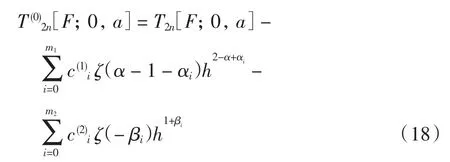
则龙贝格外推公式为

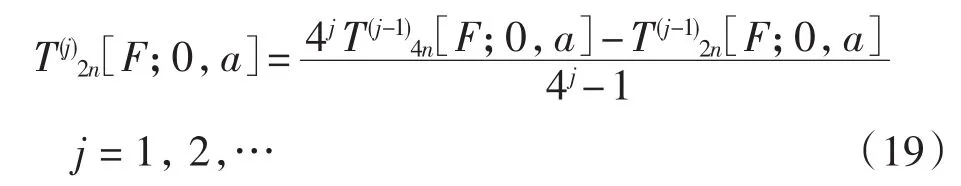
公式（19）中，精度控制要求为前后2次外推结果之差绝对值小于10-10，则可得方程（9）的高精度计算结果.

3 数值算例

例1 考虑奇异两点边值问题

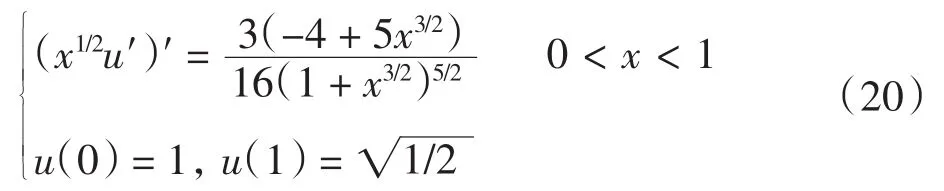
方程（20）的精确解为u（x）=1/（1+x3/2）1/2.该例中，右端项f（x）在x=0处分数阶可导，其他点处充分光滑，其精确解u（x）在x=0处仅一阶可导.利用式（12）、式（13）进行计算，并利用式（18）、式（19）进行外推，记所得数值解为uh（x）.表1给出了一些节点处的精确解u（x）和数值解uh（x）及其误差的绝对值.

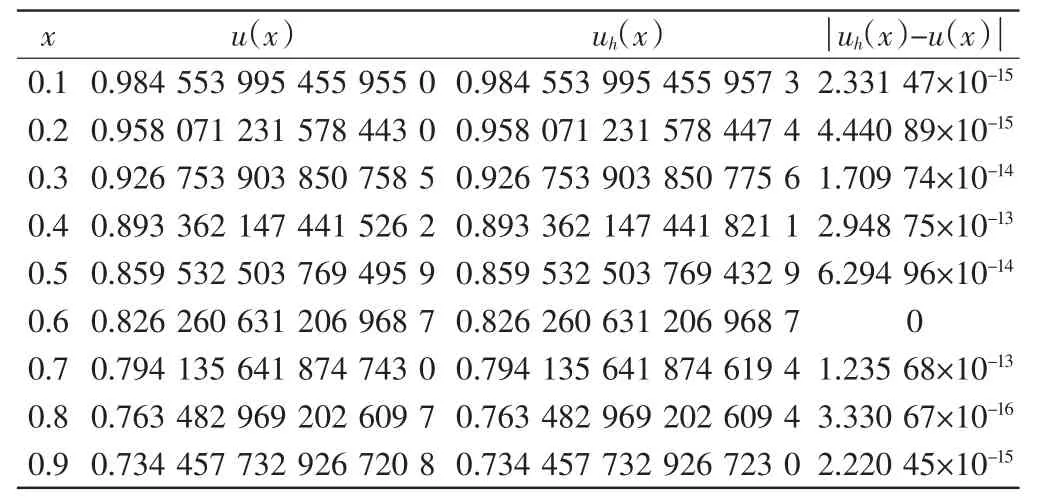
表1 例1中计算结果及误差Tab.1 Results and errors of example 1

例2 考虑两点边值问题：

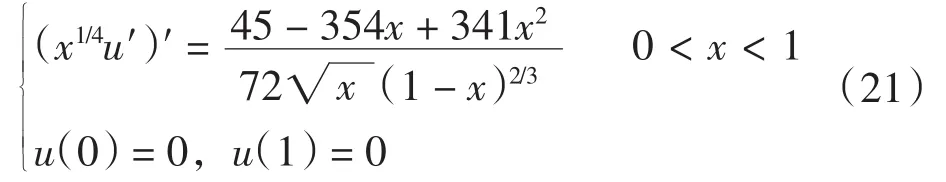
方程（21）的精确解为u（x）=x5/4（1-x）4/3.该例中右端项f（x）在x=0和x=1处均奇异，其精确解u（x）在x=0和x=1处均仅一阶可导.利用式（12）、式（16）和式（17）进行计算，并利用式（18）和式（19）进行外推.表2给出了一些节点处的精确解u（x）和数值解uh（x）及其误差的绝对值.

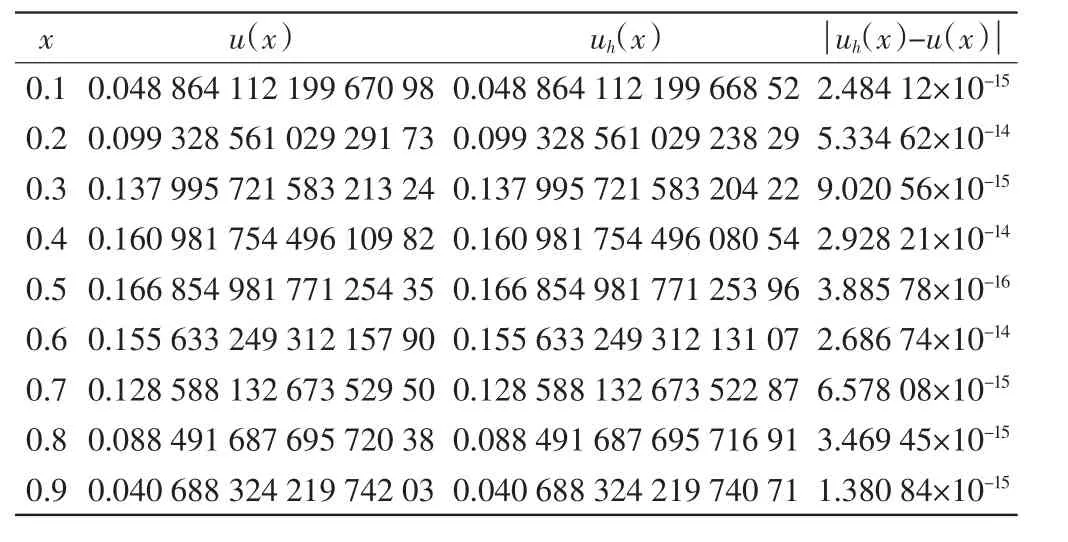
表2 例2中计算结果及误差Tab.2 Results and errors of example 2

由表1可知，例1的最大绝对误差为2.948 75× 10-13，由表2可知，例2的最大绝对误差为5.334 62× 10-14.2个算例的数值解和精确解都非常接近，优于Adomian分解法和插值方法，格式的计算效果令人满意.且由例1和例2的计算结果可知，无论方程右端的源项是否奇异，本研究方法均得到了高精度的数值结果，因此该方法对于这类奇异两点边值问题具有良好的计算效果.

[1] CHAWLA M M，KATTI C P.Finite difference methods and their convergence for a class of singular two point boundary value problems[J]. Numerische Mathematik，1982，39：341-350.

[2]韩国强.一类奇异方程两点边值问题的差分-样条校正解[J].计算数学，1991，13（2）：187-192.

[3] HAN W M.Asymptotic error expansions for numerical solutions of onedimensional problems with singularities[J].Mathematical and Computer Modeling，1991，15（12）：67-76.

[4] SINGH R，KUMAR J.Solving a class of singular two point boundary value problems using new modified decomposition method[J].ISRN Computational Mathematics，2013，23（3）：1-11.

[5] SINGH R，KUMAR J.An efficient numerical technique for the solution of nonlinear singular boundary value problems[J].Computer Physics Communications，2014，185（4）：1282-1289.

[6]STAKGOLD I.Green’s function and boundary value problems[M].New York：John Wiley and Sons，2011.

[7] CEN Z D.Numerical study for a class of singular two-point boundary value problems using Green’s functions[J].Applied Mathematics and Computation，2006，183（5）：10-16.

[8] WANG T K，LI N，Gao G H.The asymptotic expansion and extrapolation of trapezoidal rule for integrals with fractional order singularities[J]. International Journal of Computer Mathematics，2015，92（3）：579-590.

[9] PHILIP J D，PHILIP R.Methods of numerical integration[M].2nd. ed.San Diego：Academic Press，1984.

（责任编校 马新光）

Extrapolation of modified trapezoidal rule for a class of singular two-point boundary value problems

TANG Yongchao，WANG Tongke
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

High precision numerical method for singular two-point boundary value problems（SBVPs）is studied.Firstly，the SBVPs are transformed into the computation of singular integrals.Secondly，the singular integrals are discretized by modified composite trapezoidal rule and the error asymptotic expansions are obtained for some kind of cases.Thirdly，a modified Romberg extrapolation algorithm is designed to obtain high precision numerical results based on the error expansions.Finally，numerical examples show the effectiveness of the algorithm.

singular two-point boundary value problem；composite trapezoidal integration rule；fractional Taylor's expansion；error asymptotic expansion；Romberg algorithm

1671-1114（2015）04-0005-03

O241.82

A

2015-01-22

国家自然科学基金资助项目（11471166）.

唐永超（1989—），男，硕士研究生.

王同科（1965—），男，教授，主要从事微分方程数值解方面的研究.