马颖超，刘文德

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨　150025）

四维Filiform李超代数的谱序列及上同调

马颖超，刘文德

（哈尔滨师范大学数学科学学院，黑龙江 哈尔滨150025）

利用复数域上四维 Filiform李超代数的分类，通过计算，刻画了所有四维Filiform李超代数的谱序列，进而得到所有四维Filiform李超代数的上同调.

Filiform李超代数；谱序列；上同调

1　引言

在同调代数中，谱序列是一个非常重要的概念，它既是一种理论，也是研究同调模的有效方法.二战期间，J.Leray在研究代数拓扑学时，引入了层的概念，从而面临着计算层上同调的问题，为此，他提出了一种计算方法称为Leray谱序列［1］.不久，很多数学家发现，Leray谱序列只是一个特例，谱序列还应用于解决纤维化等几何问题.抽象地说，对合成函子取导函子也会得到谱序列，这样的谱序列称为Grothendieck谱序列［2］.1947年，J.L.Koszul将谱序列与代数理论有机的结合起来［3］.随着研究范围的扩大，谱序列成为计算同调的重要方法，备受国内外学者关注，现已成为同调代数、代数拓扑、代数几何、环论及群论等学科的一种有力的工具.1991年，J.A.Dixon利用谱序列计算了BRS的上同调［4］.2001年，D.W.Barnes证明了李代数的扩张的谱序列的长度最多是其商代数的维数加一，当代数是幂零的且扩张是可裂的时，谱序列的有界性能够得到一个任意大的商代数［5］.2004年，K.Kuribayashi利用Eilenberg-Moore谱序列计算了函数空间的上同调［6］.2006年，A.Romero、J.Rubio和F.Sergeraert优化了J.L.Koszul给出的计算谱序列的程序，这些程序能够计算Serre谱序列，Eilenberg-Moore谱序列等［7］.2012年，B.Edalazadeh计算了李代数的Hochschild-Serre谱序列，进而得到其上同调并给出了简化计算谱序列的方法［8］.2013年，V.J.Barco阐述了简化计算李代数谱序列的一些性质并计算了低维幂零李代数的谱序列［9］.

1970年，M.Vergne在计算幂零李代数的上同调时，提出了Filiform李代数的概念［10］.2001年，M.Gilg对复数域上维数小于等于8的Filiform李超代数进行了分类并给出了Filiform李超代数Ln，m的形变［11-12］.2006年，A.Fialowski和D.Millionschikov计算了H∗（m0）和H∗（m1）的上同调并讨论了与表示论的关系［13］.

事实上，大多数代数方面的谱序列是与滤过复形相关的.本文利用这种方法并受文献［9］的启发，计算了四维Filiform李超代数的谱序列，进而得到其上同调.

2　基本概念

设V，W 为超空间，σ：V→W 是一个线性映射.σ称为偶的，如果σ（Vα）⊂Wα；σ称为奇的，如果

Z2-分次向量空间具有双线性乘法［，］：g×g→g，称g是李超代数，如果满足以下三条：

定义 2.1［11］设是幂零李超代数，称g的超幂零指数为（p，q），如果但但其中设且称g是Filiform李超代数，如果它的超幂零指数是（n，m），记为F（n，m）.

引理 2.1［11］四维Filiform李超代数在同构意义下分为如下三类（用｛X0，X1|Y1，Y2｝表示它的一个齐次基）：

定义 2.2［14］谱序列是一个双分次Abel群族连同微分算子满足其中r∈N，p，q∈Z.

3　四维 Filiform李超代数的谱序列及上同调

利用文献［9］中的思想，即由F1，2降中心列的零化子空间构造F1，2如下滤过，令

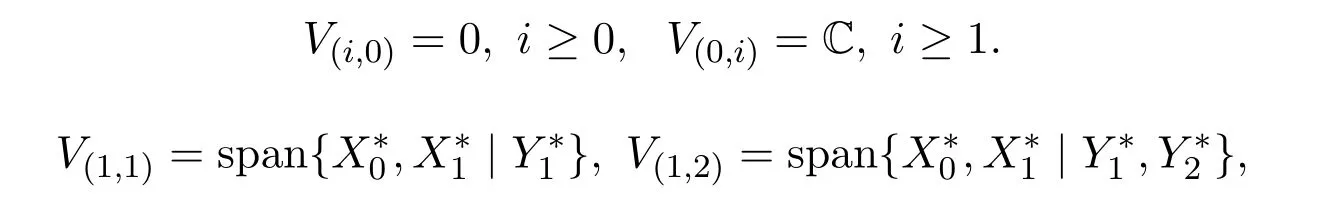
进而有表1，表2成立.

表1　V（n，1）的基及其维数

表2　V（n，2）的基及其维数

其中j≥0，u=0，1.下文不加注释的用V（n，v）表示ΛnV（1，v），v=1，2，简记F1，2=g.

表3　E0的基及其维数

其中j≥0，u=0，1，v=1，2.

证明由（6）式知，表6，表7成立.

表6　的基及其维数

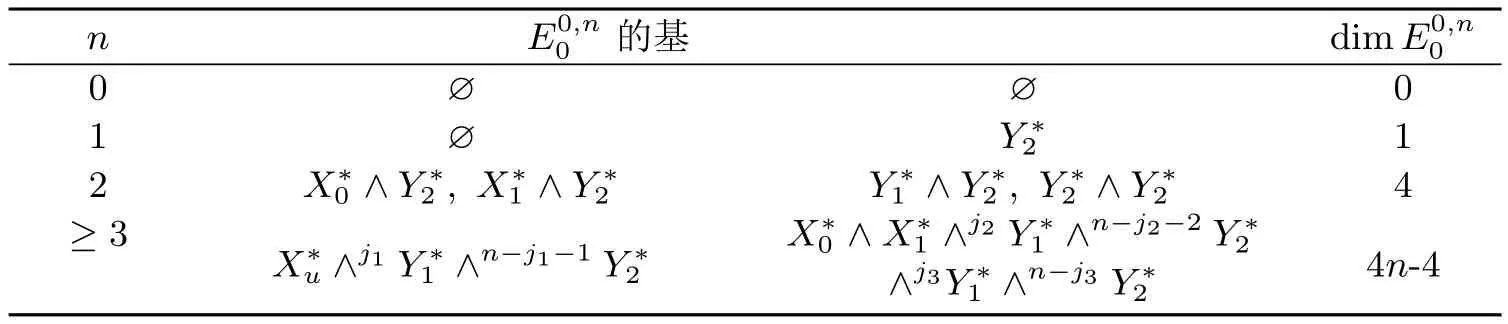
表6　的基及其维数

n E0，n0的基　dimE0，n00∅∅0 1 ∅Y∗2 1 2 X∗0∧Y∗2，X∗1∧Y∗2 Y∗1 ∧Y∗2，Y∗2∧Y∗2 4 ≥3　X∗u∧j1Y∗1∧n-j1-1Y∗2 X∗0∧X∗1∧j2Y∗1∧n-j2-2Y∗2 4n-4 ∧j3Y∗1 ∧n-j3Y∗2

表7　的基及其维数

表7　的基及其维数

n E1，n-10　　的基　dimE1，n-100 i ∅1 1 X∗0，X∗1 Y∗1 3 ≥2　X∗u∧n-1Y∗1 X∗0∧X∗1∧n-2Y∗1，∧nY∗1 4

其中0≤j1≤n-2，0≤j2≤n-3，0≤j3≤n-1，u=0，1.

由（7）式知，表8，表9成立.

表8　的基及其维数

表8　的基及其维数

n E0，n1　　的基dimE0，n10∅∅0 1 ∅Y∗2 1 2 X∗0∧Y∗2，X∗1∧Y∗2 Y∗1 ∧Y∗2 3 ≥3　X∗0∧n-1Y∗2，X∗1∧n-2Y∗1∧Y∗2　∧n-1Y∗1∧Y∗2，X∗0∧X∗1∧n-3Y∗1∧Y∗2 4

表9　的基及其维数

表9　的基及其维数

n E1，n-11　　的基　dimE1，n-110 i ∅1 1 X∗0，X∗1 Y∗1 3 ≥2　X∗u∧n-1Y∗1 X∗0∧X∗1∧n-2Y∗1，∧nY∗1 4

由（8）式知，表10，表11成立.

表10　=的基及其维数

表10　=的基及其维数

n E0，n2　=E0，n∞　的基　dimE0，n2　=E0，n∞0，1　∅　∅　0 2 X∗0∧Y∗2 ∅1 ≥3　X∗0∧n-1Y∗2 X∗0∧X∗1∧n-2Y∗2 2

表11　=的基及其维数

表11　=的基及其维数

n E1，n-1 2　=E1，n-1∞　的基　dimE1，n-1 2　=E1，n-1∞0 i ∅1 1 X∗0，X∗1 Y∗1 3 2 X∗1∧Y∗1 X∗0∧X∗1，Y∗1∧Y∗1 3 ≥3　X∗1∧n-1Y∗1 ∧nY∗1 2

表12　E0的基及其维数

表13　E1的基及其维数

表14　E2=E∞的基及其维数

其中j≥0，u=0，1，v=1，2.

证明类似定理3.1的证明可得表12，表13，表14.

表15　E0的基及其维数

表16　E1的基及其维数

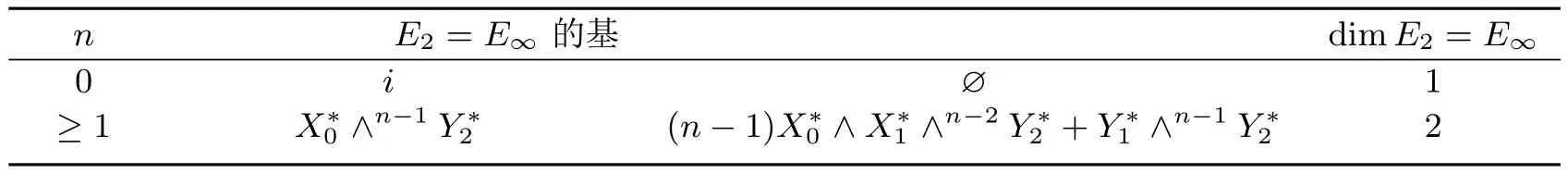
表17　E2=E∞的基及其维数

证明类似定理3.1的证明可得表15，表16，表17.

注3.1当n为奇（偶）数时，文中所有的表格的第2列为偶（奇）元素，第三列为奇（偶）元素.

由（9）式，可得到四维Filiform李超代数的任意阶同调群，于是有如下推论.

表18　的基及其维数

表18　的基及其维数

n Hn（F（1）1，2）的基　dimHn（F（1）1，2）0 i ∅1 1 X∗0，X∗1 Y∗1 3 ≥2　X∗0∧n-1Y∗2，X∗1∧n-1Y∗1 X∗0∧X∗1∧n-2Y∗2，∧nY∗1 4

表19　的基及其维数

表19　的基及其维数

n Hn（F（2）1，2）的基　dimHn（F（2）1，2）0 i ∅1 1 X∗0，X∗1 Y∗1 3 ≥2　X∗0∧n-1Y∗1，X∗0∧n-1Y∗2-X∗1∧n-1Y∗2　X∗0∧X∗1∧n-2Y∗2，∧nY∗1 4

表20　的基及其维数

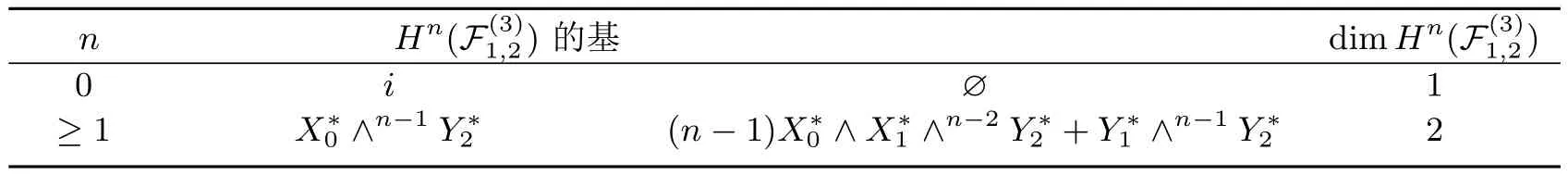
表20　的基及其维数

n Hn（F（3）1，2）的基dimHn（F（3）1，2）0 i ∅1 ≥1　X∗0∧n-1Y∗2 （n-1）X∗0∧X∗1∧n-2Y∗2+Y∗1∧n-1Y∗2 2

［1］Leray J.L′anneau d′homologie d′une représentation［J］.C.R.Acad.Sci.，1946，222：1366-1368.

［2］Weibel C A.An Introduction to Homological Algebra［M］.Cambridge：Cambridge University Press，1994.

［3］Koszul J L.Sur les opérateurs de dérivation dans un anneau［J］.C.R.Acad.Sci.Paris.，1947，225：217-219.

［4］Dixon J A.Calculation of BRS cohomology with spectral sequences［J］.Commun.Math.Phys.，1991，139：495-526.

［5］Barnes D W.On the length of the spectral sequence of a Lie algebra extension［J］.Proc.Amer.Math.Soc.，2001，129：347-350.

［6］Kuribayashi K.Eilenberg-Moore spectral sequence calculation of function space cohomology［J］.Manu.Math.，2004，114：305-325.

［7］Romero A，Rubio J，Sergeraert F.Computing spectral sequence［J］.J.Sym.Compu.，2006，41：1059-1079.

［8］Edalatzadeh B.On Hochschild-Serre spectral sequence of Lie algebras［J］.J.Math.，2012，355：61-66.

［9］Viviana J B.On a spectral sequence for the cohomology of a nilpotent Lie algebra［J］.J.Alg.App.，2015，14，ID：145007817；arXiv：1204.4123v3.

［10］Vergne M.Cohomologie des algèbres de Lie nilpotentes.Applicationà l′étude de la varièté des algèbres de Lie nilpotentes［J］.Bull.Soc.Math.France，1970，178：81-116.

［11］Gilg M.Low-dimensional Filiform Lie superalgebras［J］.Rev.Math.Compu.，2001，14：463-478.

［12］Gilg M.On deformation of Filiform Lie superalgebra Ln，m［J］.Commun.Alg.，2004，32：2099-2115.

［13］Fialowski A，Millionschikov D.Cohomology of graded Lie algebra of maximal class［J］.J.Alg.，2006，269：157-176.

［14］Musson I.Lie Superalgebras and Enveloping Algebras［M］.Rhode Island：Amer.Math.Soc.，2012，355-361.

Spectral sequences and cohomology of four-dimensional Filiform Lie superalgebras

Ma Yingchao，Liu Wende

（Department of Mathematics，Harbin Normal University，Heilongjiang150025，China）

In this paper，employing the classification of Filiform Lie superalgebras of dimension 4 over the complex field，we determine all spectral sequences of four-dimensional Filiform Lie superalgebras by means of computation.As a result，we obtain all cohomology of four-dimensional Filiform Lie superalgebras.

Filiform Lie superalgebras，spectral sequences，cohomology

O154.2

A

1008-5513（2015）03-0282-09

10.3969/j.issn.1008-5513.2015.03.009

2015-01-01.

国家自然科学基金（11171055，11471090）；黑龙江省杰出青年基金（JC201004）.

马颖超（1990-），硕士生，研究方向：李代数与李超代数.

刘文德（1965-），博士，教授，研究方向：李代数与李超代数.

2010 MSC：17B30，16E40，55T99