张节松，肖庆宪

（1.上海理工大学管理学院，上海　200093；2.淮北师范大学数学科学学院，安徽 淮北　235000）

随机累积相依索赔的矩及分布逼近

张节松1，2，肖庆宪1

（1.上海理工大学管理学院，上海200093；2.淮北师范大学数学科学学院，安徽 淮北235000）

在索赔序列具有一阶自回归相依结构的条件下，给出了随机累积索赔前三阶矩的解析表达式，并应用矩匹配的方法讨论了所得结果在总索赔分布逼近中的应用.数值实验表明了结论的正确性和有效性.

相依风险；自回归；矩；分布逼近

1　引言

经典风险模型及许多推广形式常假定索赔风险相互独立且同分布，这便于S的均值、方差、偏度系数等数字特征的获得，也可利用卷积法、矩母函数法、递推法等计算S的分布［1］，在风险理论中起着非常重要的作用.然而，现代（再）保险产品的种类和数量日渐增多，保险业务组合前期的索赔对当期索赔会产生直接的影响，学者们已越来越关注索赔风险之间的相依关系［2-7］.文献［2］采用自回归结构刻画此类相依现象，文献［3］利用线性过程描述年收益，文献［4］则假定随机保费与索赔额均具有自回归的相依结构.在此基础上，文献［5-7］进一步考虑了利率或投资收益的影响，并讨论了渐进破产概率或Lundberg上界.

与破产概率一样，随机累积索赔的矩函数是保险人所关心的重要精算量.文献［8-9］在常利率因素影响下，分别利用更新论证和鞅理论得到了现值复合Poisson风险过程的前两阶矩；文献［10-11］则在索赔次数不必服从Poisson分布的条件下推导出折现索赔复合更新和关于各阶矩的递推公式；文献［12］假定利率是随机的，并计算了更新过程和延迟更新过程的前两阶矩及协方差；文献［13］进一步将模型推广到二元复合更新情形，研究了累积折现索赔的递推矩、联合矩、矩母函数等；文献［14］考虑了索赔时间间隔与索赔量大小之间的相依关系，在索赔次数服从Poisson分布的条件下，应用Laplace变换等方法，给出了累积折现索赔各阶矩的表达式，文献［15］针对同一相依结构，应用连续逼近与Neumann级数展开的方法得到了累积折现索赔的前两阶矩；文献［16］应用文献［8，10］的技巧，导出了索赔时间间隔与索赔大小相依的Sparre Andersen风险过程折现累积索赔的矩递推公式.需要说明的是，上述工作在研究各类风险模型的矩函数时，均假定索赔风险是独立同分布的.

作为矩函数的应用之一，在累积索赔分布的矩匹配算法中，前三阶矩至关重要.文献［17］详细讨论了基于前三阶矩将一般分布映射为混合Erlang分布的方法，在索赔分布轻尾的情形下十分适用.对于重尾索赔情形，文献［18］指出应用广义Pareto分布进行逼近，但同样基于累积索赔的前三阶矩.

总结可以发现，文献［8-16］在索赔序列独立同分布的条件下，研究了随机累积索赔的矩函数，文献［2-7］则考虑了索赔序列的相依关系，但研究的是破产相关问题.受此启发，本文在索赔风险相依的条件下，考虑随机累积索赔的矩函数.假定索赔序列具有一阶自回归相依结构、索赔次数服从Poisson过程，首先计算随机累积索赔的前三阶矩，得到了与相依参数密切相关的解析表达式.然后，以索赔分布轻尾的情形为例，利用所得结果和矩匹配方法，近似计算出累积索赔的分布.最后通过数值实验进一步验证了结论的正确性与有效性.

2　自回归相依风险模型

假定保险公司在（0，t］时间内的索赔风险｛Xk，k≥1｝具有一阶自回归的相依结构，即

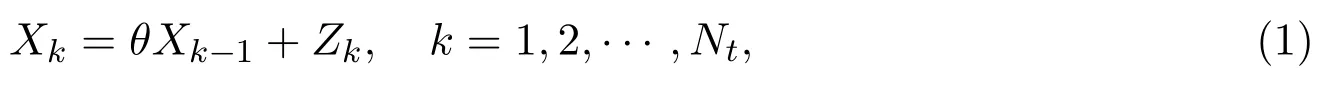
其中 θ称为相依参数，X0=x0称为初始索赔，均为常数；索赔计数过程 Nt服从参数为λt的Poisson分布；随机变量列｛Zk，k≥1｝可理解为新增业务或随机干扰项，独立同分布且非负，前三阶矩存在并记为

由（1）式不难发现，与经典风险模型中独立同分布的假定不同，这里的索赔序列具有相依结构，分布函数也不一定相同.如果特别取θ=0，即得到经典的集体风险模型.

由文献［19］可知，（1）式等价于

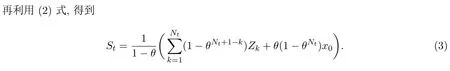
3　累积索赔的矩

有了上述φr（θ，λ），r=1，2，3的计算结果，现在根据（3）式及多项式展开给出St前三阶矩的计算结果.

定理3.1设｛Xk，k≥1｝具有（1）式所示的一阶自回归相依结构，Nt服从强度为λ的Poisson分布，则随机和St的前三阶矩分别为：

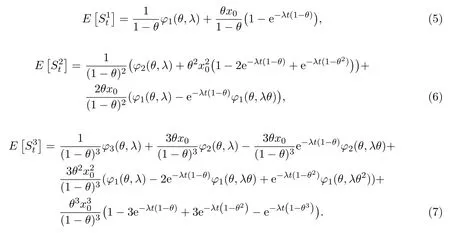
注3.1 由（5）式-（7）式可知，累积索赔风险的矩与相依参数θ密切相关，较独立同分布情形复杂很多.实际上，如果令θ=0即得到经典复合Poisson过程的前三阶矩，即λtα1，和其中m=1，2，3.

4　分布逼近

即使在索赔序列独立同分布的情形下，要计算随机累积索赔的精确分布函数，计算量也非常大，特别是个体理赔服从连续分布时，要利用常规的卷积法几乎是不可能的［20］，矩母函数法在索赔重尾情形下也可能失效.本文中的索赔序列具有相依关系且分布不必相同，随机累积索赔精确分布的计算将更为复杂，甚至难以实现.作为前述结果的应用，下面应用矩匹配（moment matching）的方法逼近St的分布.根据拟逼近分布不同的尾部特征，存在多种矩匹配的方法.当St的分布轻尾时，可选择混合Erlang分布［14］.这里参照文献［17］，采用具有相同形状参数（shape parameter）的两分支混合Erlang分布.

设共同的的形状参数为n，两分支的率参数（rate parameter）分别为λ1和λ2，则混合分布函数为：

文章最后通过具体的算例，进一步验证前述结论并观察分布逼近的效果.在给定参数下，首先运用定理3.1与矩匹配方法给出St的近似分布，然后与随机模拟的结果进行比较.

设索赔强度λ=20，Z1服从均值为8的指数分布，初始索赔x0=10，θ=0.3，t=1.根据（5）式-（7）式，借助mathematica软件计算St的前三阶矩分别为：

由此并选定n=15，计算得

于是，根据矩匹配的方法知St的分布函数可近似表示为：

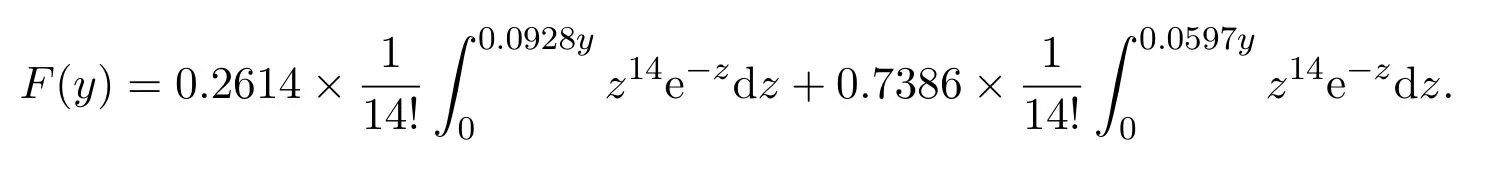
运用mathematica软件绘制出F（y）在y∈［0，400］上的图形，同时随机模拟St≤s的概率，s=1，2，···，400，得到散点图，并将二者在同一坐标系下显示，结果如图1.

从图1可以看出，利用St前三阶矩的解析表达式，并运用矩匹配方法得到的分布函数，与随机模拟的结果基本一致，特别是在St均值附近高度吻合，表明了累积索赔矩表达式的正确性及分布逼近的有效性.

图1基于矩匹配（MM）和随机模拟（SM）的累积分布函数

5　结论

本文考虑了前期保险业务组合的索赔对现在索赔的影响，以一阶自回归结构描述此类相依现象.在此条件下，推导得出了随机累积索赔前三阶矩的解析表达式.由这一结果，即可直接得到累积索赔的方差、离散系数、偏度系数等重要数字特征，还可以通过矩匹配的方法逼近随机累积索赔的分布.文章在累积索赔分布轻尾的情形下，利用混合Erlang分布示例说明了这一应用的操作方法.结果表明是有效的.实际上，当累积索赔分布重尾时，同样可利用其前三阶矩，选用逆Gamma分布、广义Pareto分布等进行逼近.这为近似计算随机累积相依索赔的分布函数带来了很大的方便.

随机累积变量的矩函数，不仅在精算实务中很有意义，也常常应用在维修成本、土木工程可靠性等其它领域.

［1］方世祖，孙歆.一类广义复合Poisson过程［J］.纯粹数学与应用数学，2009，25（1）：34-38.

［2］Bowers N L，Gerber H U，Hickman J C，et al.Actuarial Mathematics［M］.2nd ed.Schaumberg，IL：The Society of Actuaries，1997.

［3］Gerber H U.Ruin theory in the linear model［J］.Insurance：Mathematics and Economics，1982，1（3）：213-217.

［4］Yang H，Zhang L.Martingale method for ruin probability in an autoregressive model with constant interest rate［J］.Probability in the Engineering and Informational Sciences，2003，17（2）：183-198.

［5］Peng J，Huang J.Generalized Lundberg-type upper bounds for ruin probability in an autoregressive model［C］.Computer Application and System Modeling.Taiyuan：IEEE，2010：V5-650-V5-652.

［6］程建华，王德辉.Markov链利率下相依风险模型破产概率的上界［J］.吉林大学学报：理学版，2012，50（2）：173-178.

［7］Guo F，Wang D.Uniform asymptotic estimates for ruin probabilities of renewal risk models with exponential Lévy process investment returns and dependent claims［J］.Applied Stochastic Models in Business and Industry，2013，29（3）：295-313.

［8］Léveillé G，Garrido J.Moments of compound renewal sums with discounted claims［J］.Insurance：Mathematics and Economics，2001，28（2）：217-231.

［9］Jang J W.Martingale approach for moments of discounted aggregate claims［J］.Journal of Risk and Insurance，2004，71（2）：201-211.

［10］Léveillé G，Garrido J.Recursive moments of compound renewal sums with discounted claims［J］.Scandinavian Actuarial Journal，2001，2001（2）：98-110.

［11］Léveillé G，Garrido J，Fang Wang Y.Moment generating functions of compound renewal sums with discounted claims［J］.Scandinavian Actuarial Journal，2010，2010（3）：165-184.

［12］Léveillé G，Adékambi F.Joint moments of discounted compound renewal sums［J］.Scandinavian Actuarial Journal，2012，2012（1）：40-55.

［13］Léveillé G.Bivariate compound renewal sums with discounted claims［J］.European Actuarial Journal，2012，2（2）：273-288.

［14］Barges M，Cossette H，Loisel S，et al.On the moments of aggregate discounted claims with dependence introduced by a FGM copula［J］.Astin Bulletin，2011，41（1）：215-238.

［15］Mohd Ramli S N，Jang J.Neumann Series on the Recursive Moments of Copula-Dependent Aggregate Discounted Claims［J］.Risks，2014，2（2）：195-210.

［16］Woo J K，Cheung E C K.A note on discounted compound renewal sums under dependency［J］.Insurance：Mathematics and Economics，2013，52（2）：170-179.

［17］Johnson M A，Taaffe M R.Matching moments to phase distributions：Mixtures of Erlang distributions of common order［J］.Stochastic Models，1989，5（4）：711-743.

［18］Lindskog F，McNeil A J.Common Poisson shock models：applications to insurance and credit risk modelling［J］.Astin Bulletin，2003，33（2）：209-238.

［19］李炜，柳向东.自回归模型的Chover型重对数律［J］.纯粹数学与应用数学，2013，29（1）：19-24.

［20］肖争艳.风险理论［M］.北京：中国人民大学出版社，2008.

On the moments and distribution approximation of stochastic aggregate claims with dependence

Zhang Jiesong1，2，Xiao Qingxian1
（1.Business School，University of Shanghai for Science and Technology，Shanghai200093，China；2.School of Mathematical Science，Huaibei Normal University，Huaibei235000，China）

Under the condition that the claim sequence has dependent AR（1）structure，analytic expressions for the first three moments of stochastic aggregate claims are derived.The results are illustrated with applications to distribution approximations based on moment matching method.Numerical experiment shows the correctness and validity of the conclusions.

dependent risks，autoregressive，moments，distribution approximation

O213

A

1008-5513（2015）03-0252-08

10.3969/j.issn.1008-5513.2015.03.005

2014-10-02.

国家自然科学基金（11171221）；上海市一流学科（系统科学）资助项目（XTKX2012）；淮北师范大学青年科研基金（2013XQZ12）.

张节松（1981-），博士生，讲师，研究方向：保险数学，金融风险管理.

2010 MSC：97M30