裴海杰，杜宛娟

(西华师范大学 数学与信息学院，四川 南充 637009)

用观察法求二阶微分方程的非零特解*

裴海杰，杜宛娟

(西华师范大学 数学与信息学院，四川 南充 637009)

运用观察法求解二阶微分方程的非零特解.一方面对欧拉方程进行推广；另一方面对一些带有特殊系数、结构上具有某种对称形式的二阶微分方程在求取非零特解的问题进行了探讨，得到了一些相关的结论.而这些方法将有助于我们对微分方程的求解.

二阶微分方程；非零特解；特殊系数；观察法

微分方程是数学专业的基础课，更是近现代数学发展的一个重要方向.而对微分方程的求解一直都是研究的热点.基于此，一系列新方法、新手段的产生正不断丰富着微分方程的内容.用观察法求解微分方程的非零解便是其中的一个方面.文献[1]对二阶齐次线性微分方程的通解作了一定程度的探讨.作者设出相应的微分方程为f(x)y″+p(x)y′+q(x)y=0,主要针对f(x)+p(x)+q(x)=0,p(x)=-xq(x)以及p(x)=f(x)+q(x)，p(x)=0,可化为欧拉方程等五类情形进行研究.而文献[2]主要对欧拉方程推广，并运用特征方程的方法来求出非零特解，此外还给出了当方程的变系数满足某些关系时的非零特解.本文在此进一步给出欧拉方程又一推广下的非零特解，并对几类带有特殊系数的二阶微分方程利用观察法求解非零特解的问题进行探讨.期待这些结论能够为微分方程求解带来诸多便利.

1 主要结论

1.1Euler方程的推广

二阶Euler方程

x2y″+a1xy′+a2y=0

(I)

对二阶Euler方程推广，有

(1)(kx+b)2y″-m(kx+b)y′+nky=0，其中k≠0,n≠0，且m=n，则方程(I)有非零特解y=kx+b，结论显然成立.

例1 (5x+2)2y″-100(5x+2)y′+500y=0. 解 (5x+2)2y″-100(5x+2)y′+100·5y=0.由(I)知道，方程有一个非零特解y=5x+2.

(2)f(x)y″+f′(x)y=0(f(x)=kx+b,k>0)，则方程(I)有非零特解y=lnf(x).结论易证.

例2 求方程(3x+2)y″+3y′=0的一个非零特解.

解 因为(3x+2)′=3，只需令f(x)=3x+2，则f′(x)=3满足题设前提，所以该方程有一个非零特解y=ln(3x+2).

(3)如果

f(x)y″+p(x)y′-q(x)y=0

(Ⅱ)

例3 求方程3x2y″+(2x+3)y′-2y=0的一个非零特解.

(b)如果p(x)=0，且f(x)-q(x)=0,那么方程(Ⅱ)有非零特解y=ex.

例4 求方程(3x7+5x3+7)y″-(3x7+5x3+7)y=0的一个非零特解.

解 这里p(x)=0，且f(x)=q(x)=3x7+5x3+7满足条件(b),故上述方程有非零特解y=ex.

1.2 含有正余切系数的二阶微分方程

(1)形如或可变形为y″+y′(k2-1)tankx+y=0,(k≠1且k≠0)的方程有非零特解y=sinkx.

例5 求方程y″+(3tan2x)y′+y=0的一个非零特解.

解 令k=2，则(k2-1)tankx=3tan2x，由结论(1)得，该方程有非零特解y=sin2x.

(2)形如或可化为ky″-y′(k2-1)cotkx+ky=0,(k≠1且k≠0)的方程有非零特解y=coskx.

例6 求方程2y″-(3cot2x)y′+2y=0的一个非零特解.

解 令k=2，则(k2-1)cotkx=3cot2x，当然其满足(2)，所以该方程有非零特解y=cos2x.

(3)当(1)与(2)中的k=1时，相应方程等价于y″+y=0，容易知道它的两个非零特解y1=sinx，y2=cosx,并且这两个解是线性无关的,则方程的通解为y=c1sinx+c2cosx，其中c1,c2为任意常数.

1.3 带有正余弦系数的微分方程

(1)如果方程(I)有形如或者可化为y″+y′sinkx+k2coskx+ksin2kx=0,(k≠0)的形式，那么该方程有非零特解y=coskx.特别地，当k=0时，上述方程等价于y″=0，方程的通解显然为y=ax+b，其中a,b为任意实数.

例7 求解方程y″+y′sin2x+4cos2x+2sin22x=0的一个非零特解.

解 令(I)中k=2，则有y″+y′sin2x+4cos2x+2sin22x=0，由条件(I)知，该方程有非零特解y=cos2x.

(2)如果方程(1)有形如或者可化为y″-y′coskx+k2sinkx+kcos2kx=0,(jk≠0)的方程有非零特解y=sinkx. 特别地，当k=0时，上述方程等价于y″-y′=0，方程的通解显然为y=c1ex+c2，其中c1,c2为任意实数.

例8 求方程y″-y′cos2x+4sin2x+2cos22x=0的一个非零特解.

解 令(2)中k=2，则有y″-y′cos2x+4sin2x+2cos22x=0，由条件(2)知，该方程有非零特解y=sin2x.

1.4 某些在结构上具有对称性的微分方程[3]

(1)对于形如f(x)y″-yf″(x)+f(x)y′-yf′(x)=0的二阶微分方程，其中f(x)≠0，它有一个非零特解y=f(x).

例9 求方程(4x3-3x)y″-24xy+(4x3-3x)y′-3(4x2-1)y=0的一个非零特解.

解 考察函数f(x)=4x3-3x，那么f′(x)=3(4x2-1)，f″(x)=24x,与原方程系数相比较，恰好满足条件(1)，故原方程有非零特解y=4x3-3x.

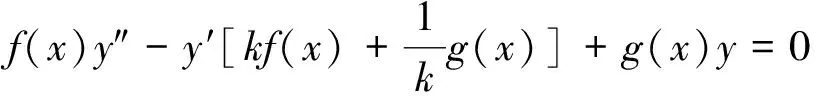
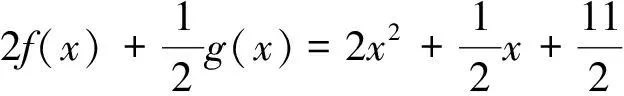
2 结束语

本文对二阶欧拉方程作了进一步推广,并得到相应的非零特解.此外还研究了带有正余切系数、正余弦系数、在结构上具有对称性的微分方程非零解问题.而许多微分方程的非零特解问题至今仍有待解决，期待更多人的加入，能得到更好的结果.

[1]李中平.用观察法求二阶变系数齐线性方程的非零特解[J].高等数学研究,2010,13(3):24-25.

[2]张清芳,库在强.用观察法求二阶变系数齐线性方程的非零特解[J].高等数学研究,2005,8(3):47-48.

[3]王高雄,等.常微分方程[M].北京：高等教育出版社,2006.

10.13877/j.cnki.cn22-1284.2015.08.011

2015-04-20

四川省教育厅自然科学项目“生物种群模型中的抛物方程解的行为分析”(14ZB0143)；西华师范大学大学生科技创新项目“非局部扩散在生物中的应用”(42714081)

裴海杰,四川广安人,西华师范大学数学与信息学院在读硕士研究生.

杜宛娟,女,四川宣汉人,副教授.

O

A

1008-7974(2015)04-0026-02