陈奎孚,李岩峰

(1.中国农业大学,北京 100083;2.解放军总医院第一附属医院,北京 100048)

从逐差法到对差法

陈奎孚1,李岩峰2

(1.中国农业大学,北京 100083;2.解放军总医院第一附属医院,北京 100048)

把逐差法组织成对差法,并以自变量差值平方为权系数进行加权平均来计算比例系数。利用初等数学方法证明了所选权函数的最优性。

逐差法;对差法;最小二乘法;偶然误差

实验所探究的物理规律,尤其是大学和中学的课程学习阶段的实验,大多是比例规律,如弹力随弹簧伸长量的变化,电压随电流的变化(电阻不变)。测量比例系数是该阶段学习的重要任务。逐差法是处理这类实验数据的常规方法,它把测量数据的因变量进行逐项相减,或按顺序分为两组后把对应项相减,最后将所得的差值进行平均以减小偶然误差。在很多中学物理参考资料中,逐差法也是处理匀加速度直线运动实验数据的推荐方法。

逐差法很经典,查中国知网可以找到北京大学普通物理教研组早在1953年的文章就有对学生用逐差法处理实验数据的要求[1]。然而随着近年来MATLAB和ORIGIN等易用计算手段的普及,在计算已不是困难的情况下(至少就高等教学而言),逐差法与最小二乘法之间的精度差异就受到了关注[2-6]。受关注的还有逐差法的计算格式和有效性。特别是,探索计算格式易于上手,因而有很多作者对主流格式进行缝缝补补[7-11]。

无论是邻差法,还是分组逐差法,操作数的选取总有一定人为随意性,这种随意性与强调追求完美的物理哲学理念形成一定反差,因而总是让人觉得心有不甘。但更遗憾的目前发表了大量反思逐差法有效性的文献[12-15],有的作者干脆认为应彻底放弃逐差法[16-17],或至少在高中阶段要放弃[18-19],或不宜过分强调[20-23]。当然也有坚持逐差法的声音[23-26]。

本研究将报告:要达到最小二乘法的精度,无需对广泛使用的逐差法计算框架进行大的变动;只要把分段逐差重组成对称相差,并进行加权修正,也能够实现最小二乘。这就在传统逐差法的手工计算与最小二乘的计算机计算之间架起了桥梁。

1 逐差法的脉络与思考

图1为某一符合比例规律的物理量测量结果示意图。

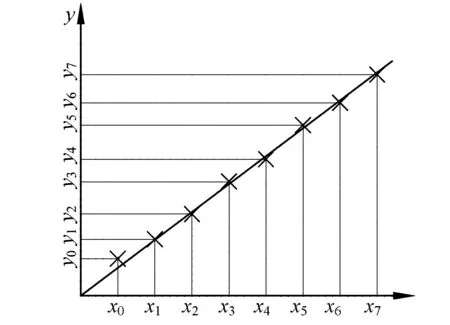
图1 物理量测量结果示意图

图1中x0,x1,X2,…,x7为自变量测量值(间距d=xi+1-xi为常数),y0,y1,y2,…,y7为因变量测量值。常规实验条件是自变量的偶然误差远远小于因变量的偶然误差,因此相对因变量而言,自变量可认为是精确的。

在计算手段比较原始的早期,我们在坐标纸上标出测量值的坐标点,然后用直尺画一条直线,让直线尽可能穿过所有坐标点。如果无法让直线穿过所有数据点,那么就让数据点在直线两侧尽可能对称分布。直线画好后,用量角器量出直线与x轴间的夹角,查数学用表的正切表,就得到了斜率,也就是比例系数。这种方式几乎不需要计算(显然其精度也不可能很高)。另外对因变量偶然误差比较大的情形,也就是数据坐标点偏离直线比较明显的情形,图解法也无法提供客观评价指标来反映比例规律对数据点的吻合程度。

逐差法是比较精确,但计算量又相对小的数据处理方法。它把8个数据中的前四个(y0,y1, y2,y3)分为一组,后四个(y4,y5,y6,y7)分为另一组,然后逐对相差,即从下式得到斜率k,

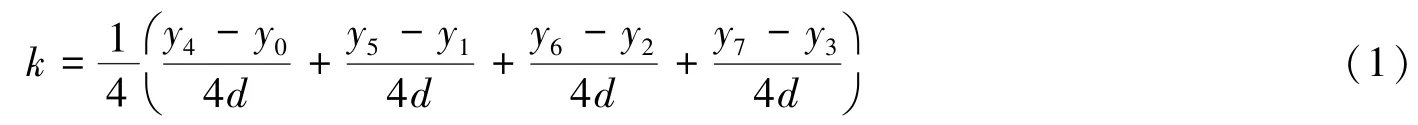
这就是所谓的两段逐差法。也有人建议使用所谓的邻差法计算斜率k,即

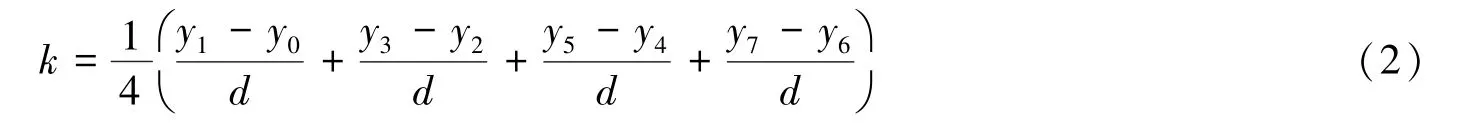
不管式(1)还是式(2)都用上了所有的测量数据,并进行了平均,似乎很完美。但显然,我们会有这样的问题:究竟是式(1)合理还是式(2)合理?(有作者认为两段法的式(1)优于式(2)[13,14])。既然有这两种方式,那么是否还存在其它更合理的计算方式?

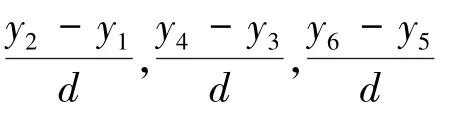
的贡献呢!?当然如果把这三项也包含进去,那就得到了

按照式(3)这样的计算,就如同文献[27],只有首末两个数据被使用了,而不是所有的测量数据。大多文章会强调式(3)没有把所有的数据都用上,而且没有平均操作,所以不宜使用。但也有实验数据支持支持式(3)优于式(2)和式(1)[28]。

下面给出优于式(1)的对差法。

2 对差法的演绎

式(1)还可以组织成如下对称相差的格式

我们记

在无偶然误差的情形下k=k1=k2=k3=k4。利用等比例性质,很容易由式(5)得到式(4)。对偶然误差存在的情形,式(4)可看作是为了抵消误差的某种平均。然而这个平均有改善的空间。

如果我们认为偶然误差分布是均匀的,那么式(5)中(y7-y0),(y6-y1),(y5-y2)和(y4-y3)的绝对误差大小是相匹配的,因为你没有理由说其中一个会比另外一个大。然而,k4误差肯定比k1的误差大。按照偶然误差均匀分布的假定,前者应该是后者的7倍。如果误差大小明显不同,那么等权平均的计算方式肯定不是最合理的。我们应该对精度高者给予更高的权重。

当然,权重选择又带来了随意性。但总的原则是,误差越大,权重越小。对k1,k2,k3,k4权重的最简单选择是7,5,3,1。如果这样选,那么就得到了式(3)。下一个容易想到的方案是72,52, 32,12,这样就有

对于任意2N个测量值的情形,式(6)扩展成通式

我们称式(7)为对称相差法,简称对差法,它将首尾相对的数据求差,再加权平均得到比例系数。其中权系数 (2N-1)2,(2N-3)2,...,12乘以就相当于d2作对差的两个自变量的距离平方。由于权系数只是一个比例系数,所示式(7)也是以自变量差值平方为权的加权平均。

为了评估式(7)的性能,我们使用近期文献发表的数据。文献选择依据是:1)原文有逐差法的处理结果;2)有公认的可信结果;3)与物理相关。经筛选,下面三篇文献比较典型(被引用的原文结果均为逐差法所得)为了避免介绍符号的物理意义,本节的计算直接用数字。需深入了解的,请参阅原始文献。

利用文献[29]的表2数据,用式(6)计算出的氩原子第一激发电位

比原文算出的U0=11.56V,更接近公认的氩原子第一激发电位11.61 V。

利用文献[30]的数据,对差法计算出的电压-电流拟合直线斜率k为

进而得到电阻率

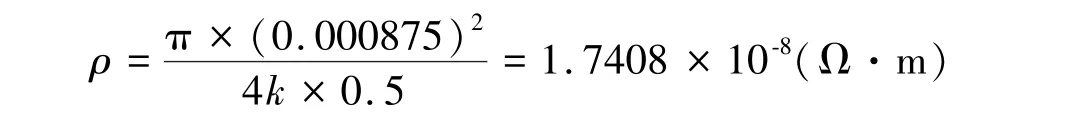
它与ρ=1.75×10-8(Ω·m)的相对误差为0.53%,而原文的相对误差1.14%。利用文献[31]的表1,对差法算出的声波波长

进而得到水的的密度

它原文的ρ=994.9kg·m-3更接近标准值ρ0=1000.0kg·m-3。

上述三个例子表明式(6)的对差法确实有效。

3 测量的优化平均

对多此测量值进行平均一般可减小偶然误差的影响,比如k1,k2是某一物理量的两次测量,我们认为(y1+y2)/2误差比y1y2小。如果两次测量工具不一样,就不能这样简单平均了,比如这里正文字体大小,用文具尺测量的长度和用全球卫星定位系统测量的长度就不能进行简单地平均,因为平均后结果的精度未必比单独用文具尺量出的精度高。不能简单平均的原因是两种测量工具的不确定度不同。

3.1 两测量值

首先有

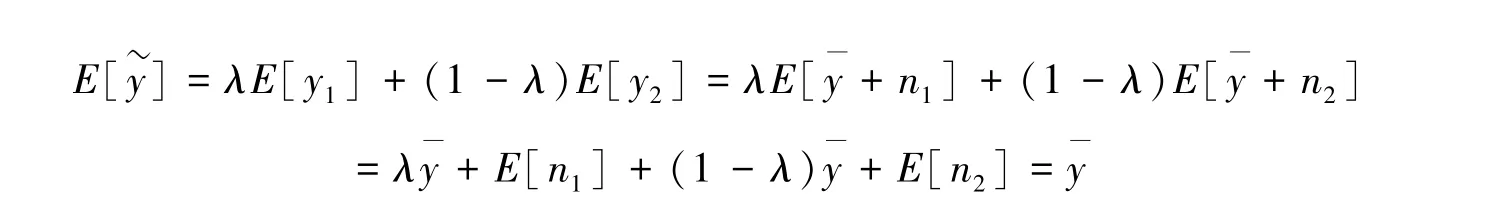
其中最后一个等号利用了偶然误差期望为0的特性了。上式表明的期望确实是真值。

因为我们假定n1,n2相互独立,所以E[n1n2] =0,这样式(8)变为

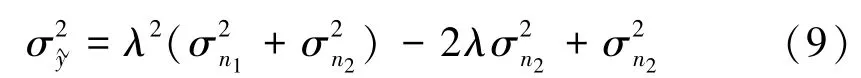
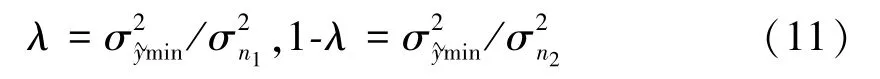
即y1,y2的优化权系数与各自的方差倒数成正比,也就是方差越大(偶然误差越大),在平均中的贡献越小。

3.2 多测量值

如果还有第三个y3=+n3,其中n3与n1,n2独立,且方差为。如何实现对y1,y2,y3加权平均得到最小的方差呢?我们先对y1,y2加权平均得到,显然的偶然误差与n3也独立,因而与y3平均就如同y1和y2的平均。与y3优化权系数分别为

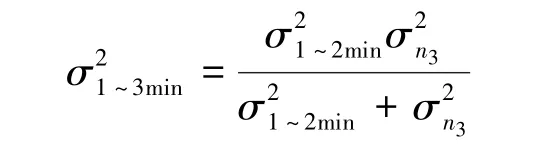
采用数学归纳法,容易证明对偶然误差相互独立的N个测量y1,y2,y3,…,yN,其优化权系数也与各自方差倒数成正比,即优化权系数为

回来看式(5),它给出了四个估计。由于假定了y0~y7的偶然误差是独立的,所以k1,k2,k3, k4的偶然误差也相互独立,因而可以使用式(13)的权系数平均。显然上述四个估计式的方差倒数之比为72∶52∶32∶12。这正是从式(5)得到了式(6)的数学依据。

以上就是对差法的数学基础,它不涉及导数和偏导数。在高中物理阶段,如果能够把期望和方差的运算解释到位,那么学生应能大体理解对差法中权系数的选择。如果没有期望和方差的概念,就只能让学生定性地接受加权平均的权系数应与不确定度的倒数成正比,即不确定度越小,测量值越可靠,在平均中贡献越大。让学生在直觉上接受这一点应该不会很突兀。

4 结 论

本文发现把逐差法重组成对差法,并以自变量间距平方加权,也能够实现最小二乘法。这就在逐差法和最小二乘法之间搭起了桥梁。

对差法适合这样的数据模型:真值部分符合比例规律,误差为独立的偶然误差。通常的匀加速度直线运动的测量值不符合这种模型,所以对差法对这种数据而言不是最优的。对差法是否改善了逐差法,以及改善的幅度需要进一步研究。

通过多次测量可以降低偶然误差,但是如果多次测量的测量工具不确定度不同,那么采用简单的平均无法减小偶然误差。此时,应采用加权平均,即不可信数据在平均中贡献要小,而可信数据的贡献要大。

有些文献认为逐差法把所有数据都用上,并且做了平均,因而误差小—这种观点是不恰当的。减小方差的严谨方法要通过对针对的误差模型用数学方法来建立。对于不具备这方面知识的学生,老师应该定性地介绍问题的相关因素。

有的作者因为逐差法不是最好的而建议放弃逐差,回到图像量斜率的原始做法—这也是不可取的。物理课程对数据处理的定量培养还是非常有必要的。作为教师,应该引导学生思考“不是最好”的影响因素,激发将来深入研究的兴趣。

[1] 北京大学普通物理教研组.北京大学普通物理实验教学经验[J].物理通报,1953(11):527-534.

[2] 潘小青.逐差法及其应用探讨[J].大学物理实验, 2010-04-26.第23(2):86-87.

[3] 夏雪琴.Matlab编程法在测量氦氖激光波长实验数据处理中的应用探索[J].大学物理实验,2015,28 (1):66-68.

[4] 李丹凤,夏雪琴.逐差法和Origin7.0软件在测量氦氖激光的波长实验数据处理中的比较[J].大学物理实验,2014,27(6):106-109.

[5] 冯学超,吴杰,蒋逢春,等.金属导体电阻温度系数实验数据处理方法的比较[J].大学物理实验, 2014,27(3):114-116.

[6] 朱国强.处理实验数据——MATLAB软件在物理教学中的应用之四[J].物理通报,2015(2):77-80.

[7] 何述平.逐差法处理打点纸带数据的研究[J].物理通报,2014(11):98-102.

[8] 赵怀彬,张中玉.应用“两段法”快速求解加速度[J].中学物理教学参考,2014,43(1-2):102-103.

[9] 单明,聂燕萍.线性拟合中的逐差法和最小二乘法的比较[J].大学物理实验,2005,18(2):68-70.

[10]张敬德.逐差法为什么会减小误差[J].中学物理教学参考,2009,38(6):16-17.

[11]张容.基于MATLAB的弗兰克-赫兹实验数据处理[J].大学物理实验,2015,28(2):100-102.

[12]卢炜杰,吴先球,王笑君.三种实验数据处理方法的误差分析和教学探讨[J].物理教学,2013,35(12): 22-23.

[13]吴小娟.应用Excel处理夫兰克赫兹实验数据[J].大学物理实验,2015,28(2):103-105.

[14]王鹏,张季谦,刁山菊.基于逐差法的测定金属电阻率实验数据处理[J].物理通报,2015(3):81-82.

[15]尹少英,刘轩,徐在春,等.基于超声波的食盐溶液物性的研究[J].大学物理实验,2014,27(3):7-10.

From Seriatim Subtraction to Symmetrical Subtraction

CHEN Kui-fu1,LIYan-feng2
(1.China Agricultural University,Beijing 100083;2.First Affiliated Hospital of PLA General Hospital,Beijing 100048)

The seriatim subtraction form is reorganized into the symmetrical subtraction form,and the proportional coefficient is estimated by weighted averaging the symmetrical subtraction with the squared argument differences being theweight coefficients.Its optimality of the selected weight coefficients is proved by elementarymathematics.

seriatim subtraction;symmetrical subtraction;least square error approach;accidental error

241

A

10.14139/j.cnki.cn22-1228.2015.005.033

1007-2934(2015)05-0118-05

2015-06-14