吴子牛*,白晨媛徐珊妹,李娟林景陈梓钧姚瑶

1.清华大学 航天航空学院,北京 100084 2.北京宇航系统工程研究所,北京 100076

翼型到达定常流动状态后,在无黏近似下其升力满足儒科夫斯基升力定理,在薄翼情况下其升力系数正比于迎角[1]。实际上翼型是通过加速达到匀速运动状态的。如果把加速时间看成无限小,那么就是突然启动问题。昆虫扑翼在每个拍动周期都有突然启动和突然停止的过程。突然启动问题在低速扑翼和可压缩流动气动弹性问题中有广泛的研究[2]。

针对不可压缩流动问题,Wagner首次用理论研究了小迎角突然启动问题[3],得出了升力系数从定常升力系数的一半逐渐增加到定常值的结论。该项基于无黏流理论得出的结论得到了考虑黏性的实验验证[4]。在小迎角突然启动过程,从尾缘拖出一个近似沿直线传播的涡层。在大迎角下,人们发现从尾缘脱落的涡,刚开始会卷曲成螺旋形状,从而导致初始升力有奇异性[5-6]。对于平板这样的具有尖前缘的翼型,在大迎角下,前缘也出现涡分离。对于这类突然启动问题,实验和数值计算[7-9]表明,除了前述升力初始奇性和 Wagner升力上升现象,还存在升力二次下降现象。对于小迎角突然启动问题,理论能给出全时间过程的升力特性预测[3]。对于大迎角突然启动问题,理论只能给出小时间的预测[6,10]。最近,Li和Wu[11]导出了可以针对全时间大迎角突然启动问题的分析方法,尤其给出了可以确定任意位置涡对升力贡献的涡升力地图。

对于可压缩流动问题,人们为了研究气动弹性,发展了小迎角下的突然启动问题分析方法[12-21]。平板突然小迎角启动时,在迎风面和背风面分别产生的压缩波和膨胀波是小扰动简单波,引起的压力和在平板上的初始升力有标准的活塞理论[12-14]。随着时间推移,这种压力波影响会快速衰减。这方面的作用也称为升力的无旋效应。同时,类似于不可压缩突然启动问题,也存在环量建立和Wagner升力上升现象,只是这种现象有可压缩性修正。在一定的假设下,Lomax[15]等给出了导出阶跃函数的方法,但针对每个马赫数其具体表达式需要单独推导；后来人们发展了许多近似方法[16-21]。

依据现有研究结果,发现不可压缩和可压缩突然启动问题研究方法相对独立,缺乏二者之间联系的分析。对于可压缩流动尤其是高超声速流动问题[22],在大迎角下,似乎没有突然启动问题报道。为了统一二者之间的关系,需要对二者现有研究现状进行综合介绍,并指出二者之间的关联和遗留的问题。为此,本文对不可压缩和可压缩突然启动问题涉及的现象和发展的研究方法进行综述,介绍现有发展动态,并指出需要进一步研究的问题。

1 不可压缩突然启动问题主要流动现象

如图1所示,在小迎角(Ao A)突然启动过程,从尾缘拖出一个近似沿直线传播的涡层。涡层总的强度与平板内部总的涡量合起来满足开尔文涡量守恒定理。在大迎角下,人们发现从尾缘脱落的涡,刚开始会卷曲成螺旋形状[5],并且导致无黏升力系数曲线初始奇性,即在零时刻,升力系数为无穷大[6]。这是因为,大迎角突然启动时,尾部涡层首先为螺旋,外部涡量贴近尾缘上部,诱导的环量的初始时间变化率为无穷大,而对于非定常问题,升力系数与环量的时间变化率是成比例的。升力系数由无穷大快速下降,达到极低值后,接着遵循Wagner升力演化曲线逐渐增加。

图1 在小迎角(Ao A)下,尾缘涡层为平面；在大迎角下尾缘涡层为螺旋[6]Fig.1 Vortex sheet is in a quasi-planar shape at small angle of attack(Ao A)and in a spiral shape at large Ao A[6]

对于平板这样的具有尖前缘的翼型,在大迎角下,前缘也出现涡分离(见图2[7])。前缘分离产生的前缘涡一方面会增强升力,另一方面,前缘涡移动到尾缘附近后,会诱导新的尾缘涡,使得升力系数出现非定常脉动。图3给出了升力系数随时间演化与典型时刻流线图[11]。升力系数遵循如下规律:①起始过程的升力下降(图3中的ab段)来源于初始奇性的逐渐消失；②升力系数第一次上升(图3中bd段)来源于尾涡的脱落与附着涡的建立,同时因为前缘涡,该段升力系数高于Wagner模型的升力系数；③升力系数的再次下降(图3中ei段)主要来源于新的集中尾涡出现,该集中尾涡来源于脱落的前缘涡平移到尾缘附近时的诱导作用,且运动指向升力减小的方向。升力系数的这种震荡会不断循环,导致一系列的峰值出现。

图2 在15°迎角时,加速运动平板前的前缘涡(LEV)与尾缘(TE)涡[7]Fig.2 Leading edge vortex(LEV)and trailing edge(TE)vortex for an accelerating plate at an Ao A equal to 15°[7]

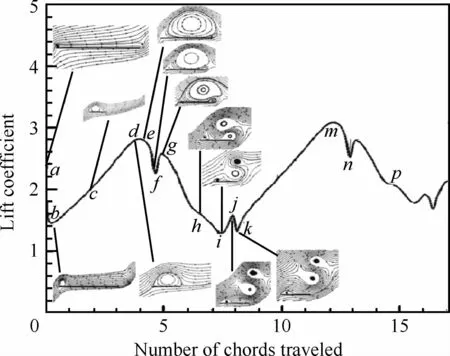
图3 迎角20°时突然启动平板的升力系数演化与典型位置的流线[11]Fig.3 Time-dependent evolution of lift coefficient for an impulsively starting plate at Ao A of 20°[11]

在第2节、第3节和第4节中,将分别给出小迎角和大迎角下的分析方法。为此,先介绍相关符号约定,并简要介绍旋涡的基本作用。约定翼型从静止突然以速度V∞和迎角α向左平动。如果将坐标系固定在翼型上,V∞就是启动后从左向右的来流速度。升力L定义为垂直于翼型平动方向也就是垂直于来流方向的力。

在无黏框架下,定常二维流动的翼型所受的力只有升力,即垂直于运动方向。而在非定常情况下,这种无黏的气动力F有可能并不垂直于来流方向。因此,以下的内容将严格说明力的进一步定义。升力系数定义为

式中:ρ∞为远方空气的密度。突然启动问题涉及的升力与流场结构与时间t有关。对于小迎角问题,有时也用到升力系数斜率CLα=d CL/dα。

定义无量纲时间为

该时间等价于当前时刻翼型以速度V∞移动的弦长cA的个数,是突然启动问题涉及的无量纲时间。在第5节会进一步讨论其他形式的无量纲时间。

在突然启动问题的非定常流场中,一般存在初始时刻甚至后期时刻从尾缘甚至前缘脱落的涡。虽然从严格意义上讲,涡是连续生成的,但为了研究方便,会将连续分布的涡尤其是集中的涡量区用点涡表示。作为约定,某点涡(指标用i)的强度Γi以逆时针为正,顺时针为负。尾缘产生的涡一般为逆时针(Γi＞0),前缘产生的涡一般为顺时针(Γi＜0)。绕翼型的环量也是按这种符号约定。

将点涡的序号记为i=1,2,…,各点涡的坐标记为(xi,yi)。它们在流场中任意一点(x,y)诱导的速度为

式中:ri=为点涡i与当前位置的距离。根据Bai等[23],流场内部的点涡以及翼型内部的镜像涡引起的单位展长上的升力可以表示为

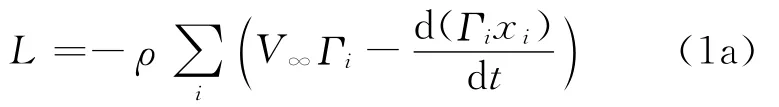
这里每个求和项都是针对物体内部和外部所有的点涡求和并且必须假设Kelvin定理满足,即系统中(包括流场内部和翼型内部)的点涡的总的环量为

对于连续分布的点涡,可以将式(1a)写成积分形式[24]:

式中:ω=ω(x,y)为涡量分布函数,可以用Dirac函数与点涡强度关联。式(1)右端第1项就是定常流动的升力,即由儒科夫斯基升力定理:

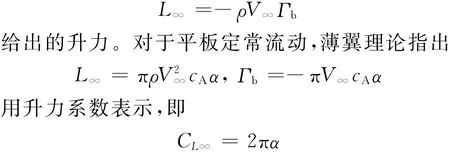
文献[23]和文献[24]从式(1)出发,还给出了多物体流场中单个物体的力的表达式。

对于突然启动问题,在达到定常状态之前,环量Γb是一个逐渐建立的过程,并且前缘和尾缘发出的涡会通过式(1)的右端第2项改变升力。到底是增加升力还是减小升力?并且,升力如何随时间演化?这些演化与外部点涡的关系是什么?这些问题是突然启动问题需要考虑的。

2 小迎角不可压缩问题:经典Wagner问题

2.1 Wagner问题经典解

如图4所示,平板在小迎角下突然启动后,在尾缘会拖出涡层。同时,绕平板逐渐建立环量Γb。如果用涡量分布函数来描述绕平板的环量和涡层强度,那么可以在平板上布置连续分布的强度为γ(x)的点涡,在涡层上布置强度为k(s,t)的点涡。

设s为从尾缘开始沿着涡层切向的距离。作为小迎角下满足的近似,令涡层内部没有相互诱导,并且在当地的流速近似等于来流速度。于是,涡层分布在直线段0＜s＜V∞t上并且满足涡强质点导数为0(开尔文涡强守恒定理)的条件:

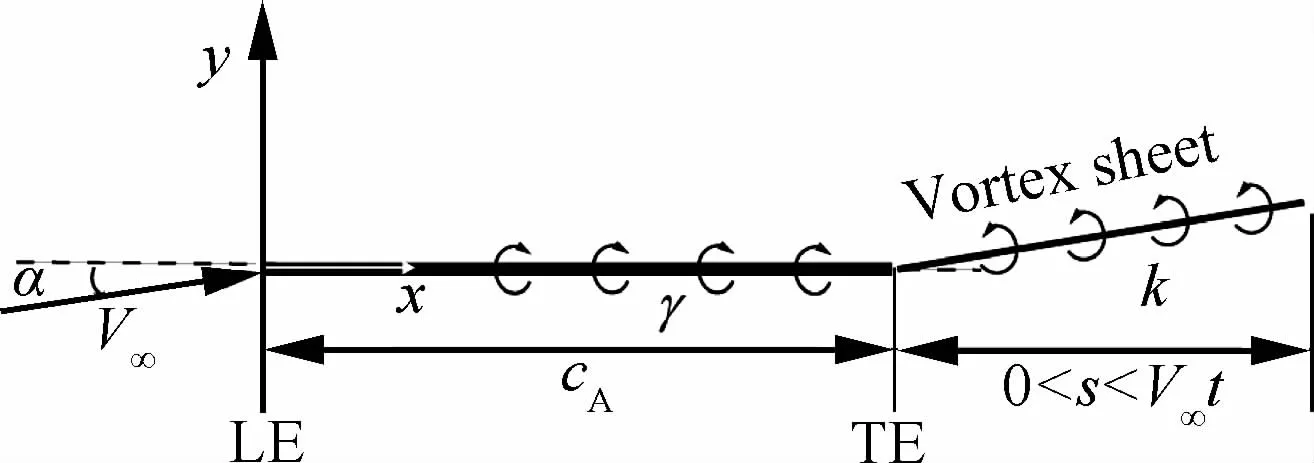
图4 平板小迎角突然启动后的涡分布Fig.4 Vortex distribution for an impulsively starting plate at small Ao A

按照开尔文总涡量守恒定理,平板内的总涡量与尾涡涡层的总涡量合起来等于0,于是

在时刻t外部存在一段分布在0＜s＜V∞t的涡层,其在平板上的诱导速度被平板上的点涡诱导速度平衡,利用薄翼理论不难证明,这样的平衡关系给出[23]

从以上两个式子消去Γb,便得到如下确定k(s,t)的方程:

该方程的解没有解析表达式,但Wagner[3]给出了数值解。文献[11]给出了如下拟合表达式:

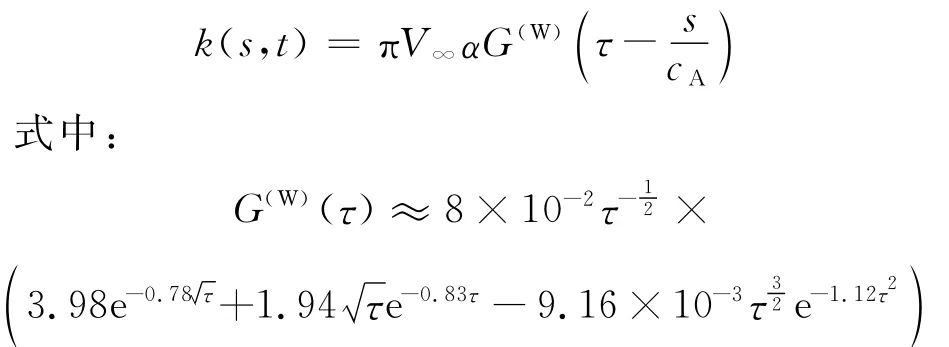
有了k(s,t),按式(2)就可以得到环量表达式Γb=-πcAV∞αF(W)(τ)。这里F(τ)称为环量的Wagner函数。文献[11]结合现有的表达式拟合出

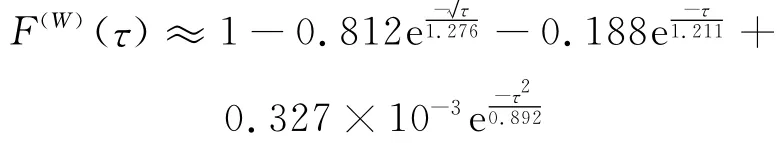
该拟合表达式满足理论上可以证明的渐进规律:

即在初始时刻,虽然环量为0,但其变化率为无穷大。这就导致初始时刻的升力系数是不为0的有限值。对于本问题,将升力的表达式(1)用到涡量沿直线分布的情况,可以将升力表示为

利用考虑了涡层影响的薄翼理论,可以求出γ的表达式,详细表达式见文献[24]。有了γ和k(s,t)的表达式后,就可以求出升力。经过推理,该力的表达式也可以写成[24]

但没有解析表达式。Wagner[3]给出了如图5所示的数值结果。

图5 突然启动问题Wagner给出的原始曲线[3]Fig.5 Curves given by Wagner for impulsively starting flow[3]

为了方便使用,人们将Wagner问题的升力写成

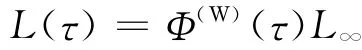
式中:L∞为定常状态下的升力；Φ(τ)为升力的Wagner函数。人们针对Wagner函数进行了各种拟合,其中最简单的拟合表达式为Garrick表达式:

Garrick公式误差不到2%。Jone给出的拟合表达式为

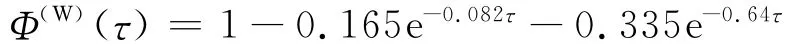
综上所述,小迎角突然启动问题(Wagner问题)有如下结论:

1)初始时刻的环量为0但环量变化率为无穷大。

2)初始时刻的升力系数为定常升力系数的1/2。

3)在无量纲时间为7时,升力系数达到定常升力系数的90%。

4)环量和升力随时间沿着单调增长的Wagner函数变化。

翼型突然启动后,建立环量必然伴随着旋涡从后缘脱落的过程,需一定的时间才可以完成,这就是所谓的Wagner滞后效应。Wagner的结果可以这样总结,对于小迎角突然启动的薄翼,虽然附着涡的初始环量为0,但初始升力却等于定常升力的一半。翼型的环量和升力随着时间按Wagner函数F(τ)和Φ(τ)规律逐渐增加,在无量纲时刻等于7,即翼型移动了7个弦长时,升力达到了最终定常升力的90%。Wagner的结果在1931年被 Walker用实验证实[4]。

2.2 Wagner经典问题的简化分析

当翼型外部有点涡时,可以简单地把翼型本身看成一个点涡。在这种简化处理框架下,翼型所受的升力可表示为[25]

式中:us为所有外部点涡(甚至包括其他物体)在翼型中点的诱导速度。文献[25]用两个集中涡分别替代附着涡和尾涡层,得到了Wagner问题的简化解析表达式。假设处在平板中心x=xb的集中附着涡涡强为Γb(t),处在位置x=xs的尾涡涡强为Γa(t)=-Γb(t)。尾涡在平板中点的诱导速度为

在该诱导速度修正下,平板等效迎角不等于几何迎角。考虑到这种修正并依然使用薄翼理论,得附着涡的环量表达式为

在初始时刻,启动尾涡位置为xs(0)=cA,并且令该启动尾涡以速度d xs/d t=V∞运动。于是xs=cA+V∞t。将此代入式(4)可解得

式中:Γ∞=-πcAV∞α为定常流动附着涡的环量。由于处在水平面的尾涡在平板中点诱导的水平速度近似为0,因此按式(3)得

这与Wagner的结果完全一致。

3 可压缩小迎角问题:活塞理论与阶跃函数法

3.1 初始气动力的活塞理论

由文献[12]提出的活塞理论,可以给出在可压缩流体中翼型小迎角突然启动时初始压力分布和初始升力。先回忆一下特征线理论中的小扰动简单波理论。在小扰动情况下,可压缩流动的某些物理量在某一区域可能是常数。其中,最典型的是黎曼不变量:

式中:下标∞表示某参考点的流动参数；V和a分别为当地流速和声速；γ为比热比。由该式可以解出

由于假设是小扰动从而是等熵流动,所以压力可表示为

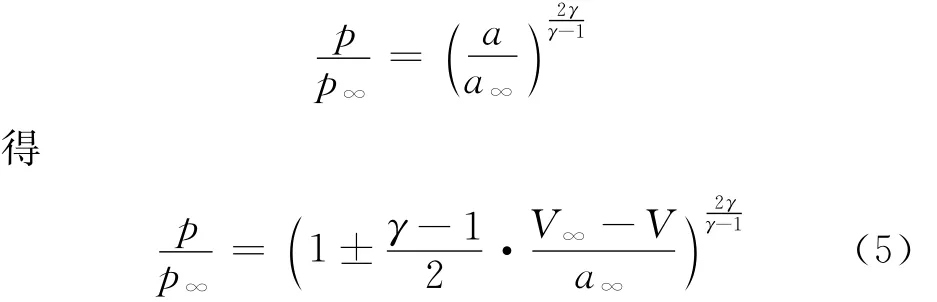
在均匀流场中,小扰动导致的流场,一般至少满足其中一个这样的关系式,这种关系称为简单波关系。活塞理论把翼型的突然启动看成沿物面法向有大小等于

的小扰动。这种小扰动激发的流动是简单波,从而导致的压力变化,按式(5)得

针对更一般的情况,Lomax等给出了更为复杂的表达式。图6[15]给出了Lomax等理论得到的升力系数斜率随无量纲时间的变化曲线。在文献[26]中,Bai等针对马赫数Ma∞=0,0.5,0.8用CFD做了计算(见图7),发现结果与文献[15]的理论结果吻合得非常好。

其中正负号可分别用在迎风面(增压)和背风面(降压)。式(6)即为气动弹性问题中计算突然运动引起的瞬间气动力的活塞理论。其引起的初始时刻的法向力系数为

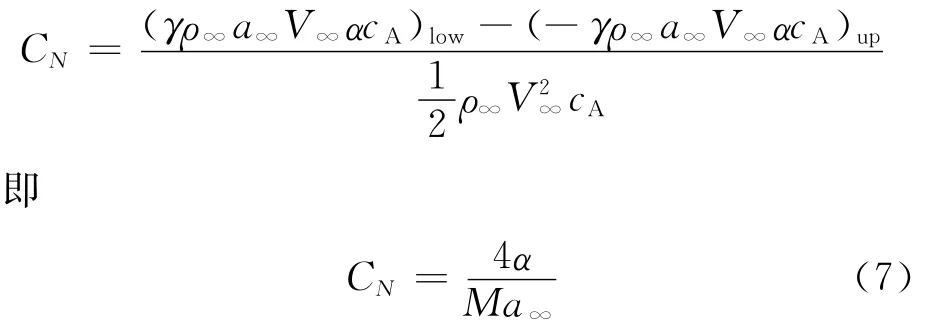
式(7)就是气动弹性理论中用于计算瞬间位移引起的气动力修正的活塞理论[12],可以用到从亚声速到超声速情况下的任何马赫数[12-14]。这里Ma∞=V∞/a∞为来流马赫数。

3.2 气动力演化的阶跃函数法

Lomax等[15]用小扰动线性波动方程,给出了计算突然启动等问题的非定常升力计算方法,并且针对几个特殊马赫数,给出了具体表达式和曲线。在无量纲时间满足

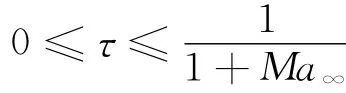
的初始阶段,升力系数近似线性下降,表达式为

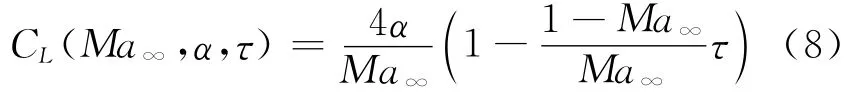
在不可压极限情况下,针对0≤τ≤∞,升力系数由Wagner解给出

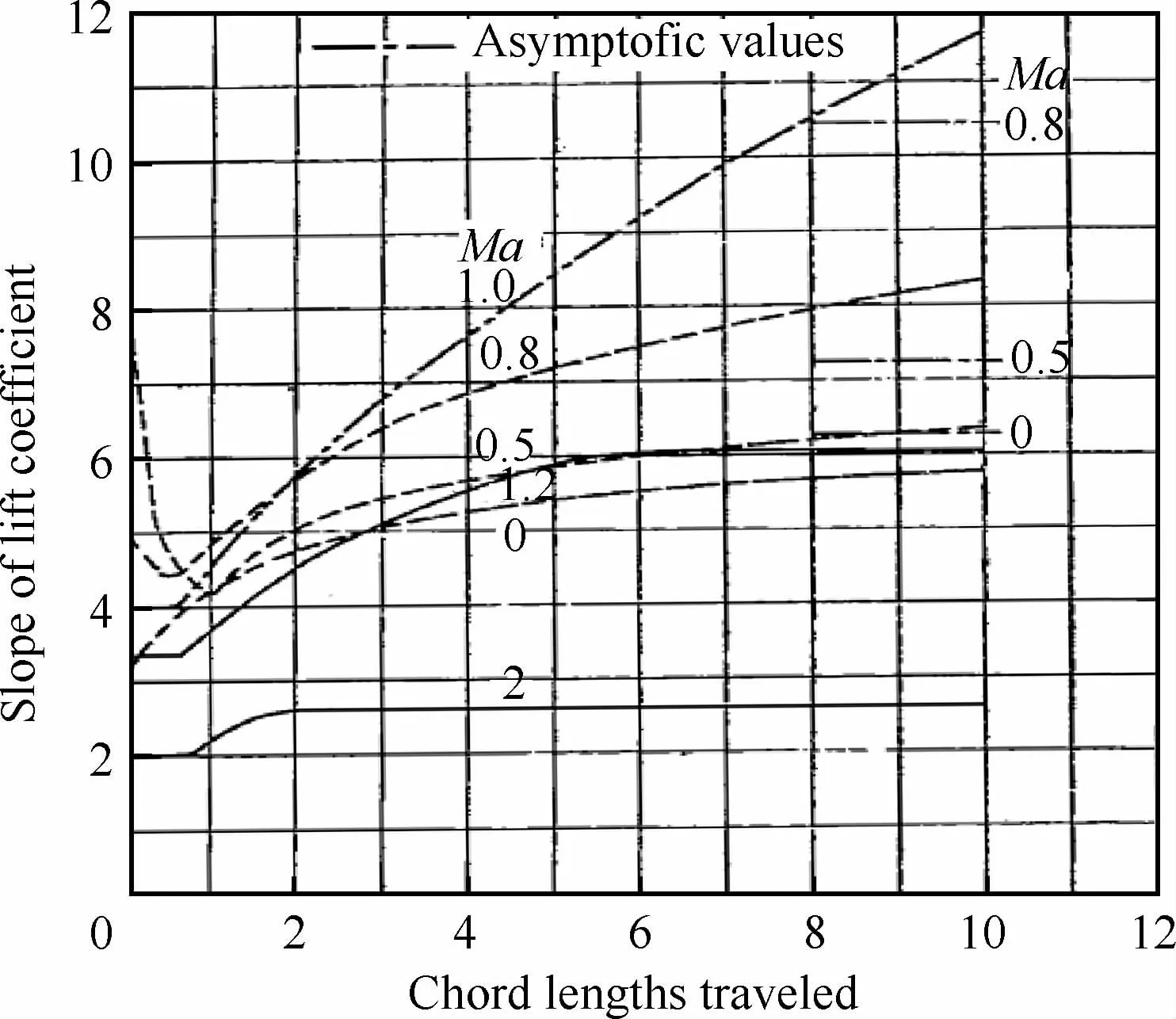
图6 可压缩突然启动问题的升力系数斜率CLα=d CL/dα随无量纲时间的变化率[15]Fig.6 Time-dependent evolution of slope of lift coefficient CLα=d CL/dαfor compressible starting flow[15]

图7 不同马赫数下可压缩突然启动问题的升力系数斜率CLα=d CL/dα随无量纲时间的变化率[26]Fig.7 Time-dependent evolution of slope of lift coefficient CLα=d CL/dαfor compressible starting flow[26]at different Mach numbers

作为近似处理,对于更一般的情况,可以将升力系数写为[16-18]

式中:Φ(I)、Φ(C)为阶跃函数；β=1 - Ma2∞为普朗特-葛劳沃特(PG)可压缩性修正因子。第一个阶跃函数Φ(I)(τ)与环量无关,来源于活塞效应及其衰减(non-circulatory part)；第二个阶跃函数Φ(C)与环量有关,来源于流场中涡量场以及绕翼型环量的贡献,在不可压缩特殊情况,就是Wagner函数,即

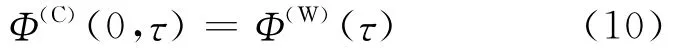
另外,在小时间步的情况下,式(9)应退化为式(8),即

在满足约束关系式(10)和式(11)的条件下,人们依据实验或数值计算结果,拟合了阶跃函数的一些近似表达式。例如,Leishman[16]令

经验算,发现这种做法对于突然启动问题,结果在τ=O(1)左右的误差较大。一种改进做法是,令

并令式(11)的各阶导数在τ=0成立,得ϑ(τ)满足的几个关系式,再将ϑ(τ)写成含有几个系数的指数函数,就可以通过定出这几个系数来拟合。这个问题需要进一步研究。

4 不可压缩大迎角问题:修正的Wagner函数法与涡力线理论

4.1 小时间升力特性

对于小迎角下的突然启动问题,尾部拖出的涡层近似分布在一个平面上,而对于大迎角问题,尾部拖出的涡至少在初始时刻会卷曲成螺旋涡(见图1)。与小迎角Wagner问题的初始升力为定常升力的一半不同,这种螺旋涡的诱导作用使得初始升力为无穷大。Graham证明[6],初始时刻的升力系数急剧下降,满足关系式:

式中:k=2-ϑtr/π,ϑtr为尾缘角。对于尾缘角为0的平板,有

Pullin和Wang[10]考虑了尖前缘的情况。此时,无论是尾缘还是前缘,都有螺旋涡拖出,如图8所示。

图8 大迎角突然启动与加速问题的前缘涡与尾涡[10]Fig.8 Impulsively starting flow at large Ao A having both leading and trailing edge vortices in spiral shape[10]

在时间足够小的情况下,突然加速所受的力F垂直于平板并且平板法向力满足

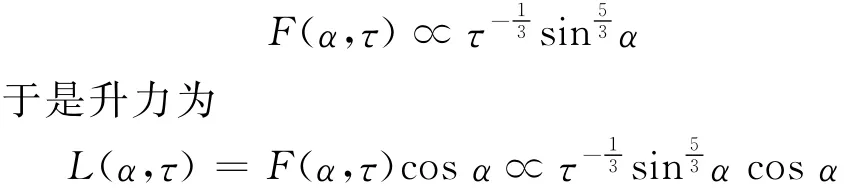
令该升力表达式对迎角的导数等于0,文献[6]得到的最大升力系数对应的迎角为

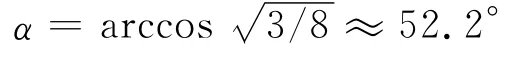
据此他们认为昆虫近似采用这么大的迎角飞行,以便获得最大升力。

4.2 长时间修正的Wagner函数法

对于长时间行为,Li和Wu[11]用图9近似真实情况,即假定有前缘涡、在时间为0＜τ＜τ0的初始阶段有螺旋尾涡在尖尾缘,在时间τ0＜τ＜τ1拖出的尾涡又近似在一个平面上。

图9 大迎角突然启动问题的前缘涡与尾涡[11]Fig.9 Leading edge and trailing edge vortices for starting flow at large Ao A[11]

将前缘涡和初始尾涡看成两个或多个额外的离散涡,得到了这样的升力表达式,即

修正的Wagner函数比原始Wagner函数小。道理很简单,因为初始时间段的尾涡被卷曲,已经算到式(12)右端第2项了。在右端第2项中,I为额外点涡即附加涡的个数,包括前缘涡和初始时刻的卷曲尾涡(即时间τ0＜τ＜τ1段平面涡层外的所有涡,无论是看成集中涡还是看成一系列的点涡)。另外,U(i)为点涡的移动速度,ΛA=[PAQA]为附加涡的涡力线矢量,OA、PA和QA为附加涡升力因子,其表达式分别为

依据表达式(12)的分析表明,处在前缘附近的前缘涡(顺时针)引起的附加涡升力,将原始的Wagner曲线抬高。这就是前缘涡增强机制的本质原因。但是,这项研究表明,前缘涡远离前缘后,并不再增强升力。

4.3 长时间涡力线方法

表达式(12)并不能用于处理τ＞τ1的情况。此时,从尾缘有其他的螺旋涡脱落出。文献[11]研究表明,在迎角足够大后,前缘集中涡一旦脱落并且移动至尾缘附近,那么就会导致产生第二个螺旋尾涡,此时表达式(12)不能继续使用。为了考虑更一般的情况,文献[11]将所有的涡(包括可能存在的平面涡层)看成离散点涡。假设流场中一共有I这样的离散涡,那么升力可表示为

式中:ΛB=[PBQB]为涡升力线矢量；为涡升力线角,表示速度矢量U(i)(与问题相关)与涡升力矢量ΛB(与问题无关)之间的夹角。这里,PB=PB(p,q)、QB=QB(p,q)均为与时间无关的总涡升力因子,定义如下:

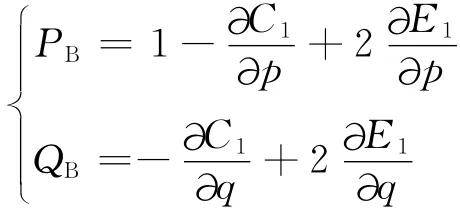
文献[11]给出了用于定性分析点涡对升力贡献的涡升力线图(Vortex Force Line Map),文献[27]对此图进行了修正,见图10。

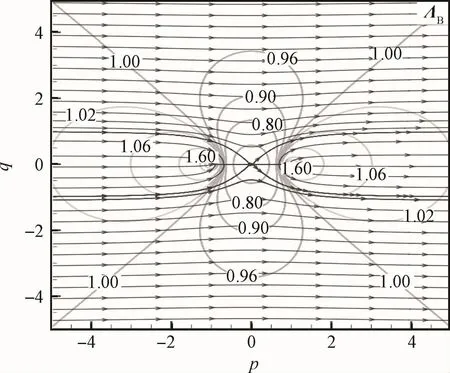
图10 涡升力线图[27]Fig.10 Vortex force line map[27]

图中带箭头的曲线类似于流线,即将流线中的速度矢量用涡升力线矢量ΛB替代。不带箭头的曲线代表ΛB的等值线。在涡升力线图中,存在一条特殊的升力线ls,在平板中间点x=cA/2(p=0)位置穿过平板。考虑上半部分,即q＞0的区域,ls左侧的总升力线在平板前缘处汇聚成一点,而ls右侧的总升力线在平板尾缘处汇聚成一点。文献[11]还有另外一条临界线,标记为lm,此处ΛB≈0.707,经过验证,其实不存在这条临界线。ΛB在靠近前缘的地方很大(前缘敏感区),在靠近尾缘的地方也会变大(尾缘敏感区),在尾缘点处ΛB的值无穷大。当涡进入这些敏感区的时候会诱导出很大的升力或者是升力的变化。这就是为什么初始时刻螺旋尾涡产生时,升力为无穷大并且快速下降的原因。依据表达式(13)并结合图10,有如下结论[11]:

文献[11]正是基于这种方法,用基于离散涡模拟或CFD模拟得到涡场后,解释了大迎角下各种升力下降、上升与再次下降的详细过程。其中一个重要结果是,对于20°迎角平板突然启动问题,前缘涡脱落移动到尾缘附近(按图10,导致升力下降),会诱导出一个螺旋涡临时向上游移动(按图10,进一步导致升力下降),导致升力系数有大幅度的下降(见图3)。这就是固定翼飞行很难采用大迎角的原因。文献[10]只给出了20°迎角的计算结果分析；文献[27]推广到了更高迎角的情况。依据文献[27]的结果,对于更高迎角,涡力线模型(式(13))能较为准确地预测平板所受的法向力。

5 结果讨论与存在的问题

以平板翼型为例,突然启动问题的现有研究可以总结如下:

1)小迎角不可压缩突然启动问题。尾部连续拖出涡,涡层近似为平面形状；针对所有时刻有精确解但升力系数和环量随无量纲时间τ=V∞t/cA的演化规律只能给出拟合表达式。初始升力等于定常升力的1/2,这来源于初始时刻环量的变化率(环量变化率也贡献升力),虽然初始时刻的环量为0。在翼型移动7个弦长的距离(即τ=7)后,升力系数为定常升力系数的90%。

2)小迎角可压缩问题。初始时刻有压缩和膨胀小扰动波分别在迎风面和背风面产生；其法向流动可按一维活塞理论处理；这种小扰动波的产生导致初始升力系数反比于马赫数(CL(0)=4αMa)；随着时间推移,类似于不可压情况的环量的建立,导致升力系数先近似线性变化(亚声速时线性下降,超声速时可能线性上升),接着逐渐上升,最后趋向于定常解(即儒科夫斯基升力定理加上普朗特-葛劳沃特可压缩性修正)。在一些文献上,活塞效应及其衰减以及环量效应被分成两部分单独处理,并采用不同的拟合函数(阶跃函数)。

图11 升力系数随时间的演化[26]Fig.11 Time-dependent evolution of lift coefficient[26]

3)不可压缩大迎角问题。在初始时刻,尖尾缘有螺旋涡产生,导致初始升力系数为无穷大并随时间推移快速衰减；当这个螺旋尾涡脱落后,新拖出的涡近似可以看成平面涡层(与小迎角时类似),升力系数随时间逐渐增加；如果是尖前缘,那么尖前缘处也有涡脱落；前缘涡在前缘附近时,使得升力系数曲线高于经典 Wagner曲线,如果前缘涡移动到尾缘附近,则引起升力下降,进一步如果诱导出新的尾涡,那么升力系数会急剧下降；文献[10]提出的涡升力线图能用于有效刻画点涡对升力变化的贡献。

平板以外的翼型以及黏性等对上述结果有定量修正但定性结果依然成立。从现有文献可以看出,可压缩大迎角突然启动问题,缺乏分析理论和结果。在文献[26]中,Bai等针对马赫数Ma∞=0.5,0.8,0.9用CFD做了20°迎角时的计算,发现结果与图3那样的不可压缩流动结果相比有一定的相似性。其中针对亚声速突然启动问题的一条重要结论是,在升力系数上升的起始阶段,马赫数越高升力系数越小,这与可压缩性效应提高升力系数有矛盾,因此需要进一步研究。文献[26]也计算了马赫数为1.5时的超声速大迎角突然启动问题,如图11(a)所示。可见,在这种条件下,升力系数不像亚声速那样有震荡,而是比较单调地变化。原因在于,在这样的条件下,没有明显的涡脱落。

图11(b)给出了高超声速条件下(Ma∞=8.0)平板大迎角突然启动问题的升力系数。发现,在极短的时间内,即达到定常解。但是,在初始时刻,升力系数先急剧上升,达到某个峰值,再急剧下降。这一结果与图11(a)所示的低超声速结果有明显差异,具体原因有待进一步分析。

4)特征时间。对于突然启动问题,人们一直采用特征时间τ,但图6、图7和图11表明,升力系数演化的第一阶段(近似线性阶段)的结束时刻τ似乎与马赫数Ma∞有关系。为此我们定义三个无量纲时间,即基于波速的无量纲时间:

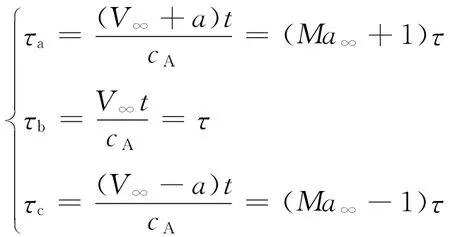
它们分别是最快运动的小扰动波在当前时刻移动的弦长个数,以对流速度运动的小扰动波在当前时刻移动的弦长个数和最慢运动的小扰动波当前时刻移动的现象个数。这里,λ1=V∞+a是第三简单波对应的速度(特征值),λ2=V∞是对流速度,λ3=V∞-a是第一简单波对应的速度(特征值)。流动特性与升力曲线演化特性与这三个特征时间的具体关系,需要进一步研究。

实际应用很难做到真正的突然启动,即翼型或机翼很难瞬间获得最终速度(否则意味着初始时刻的加速度是无穷大),而是需要一个初始加速过程。此时V∞=V∞(t)。这一加速过程带来两个方面的影响:

1)附加惯性力。附加惯性力与加速度成正比,处理方法见文献[7,9,10,23]以及其中引用的参考文献。例如,平板的附加惯性导致的升力为

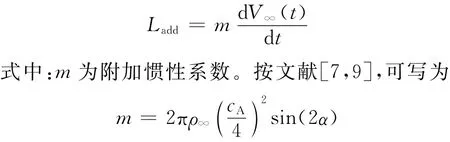
2)历史效应。文献[10]将 Wagner经典理论用于加速平板时,针对每一时刻的当前速度,直接套用原始Wagner公式。在文献[7,9]中,也并没有考虑加速过程历史效应的累计影响。但在气动弹性阶跃函数研究中,历史效应用Duhamel法则[17,28-29]计入(却不计入附加惯性力)。例如,对于小迎角不可压缩任意运动问题:

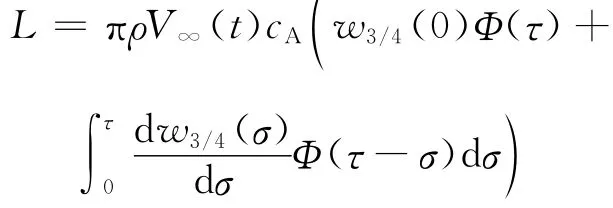
式中:w3/4=w3/4(τ)为3/4弦长处的下洗速度。对于定常问题,下洗速度就是来流速度被带迎角的翼型向下折转了速度分量。对于平板定常流动,w3/4(∞)=V∞(∞)sinα,Φ(∞)=1,因此

即退化为儒科夫斯基升力定理给出的升力。

附加惯性效应和基于Duhamel法则的历史效应为何在两类文献中并不同时出现,也是一个需要进一步考虑的问题。

6 结 论

本文对突然启动问题涉及的流动现象、升力演化规律和分析方法进行了综合介绍。过去人们将不可压缩和可压缩突然启动问题看成不同问题进行研究,本文首次将二者进行比较性研究。研究结果表明:

1)对于小迎角突然启动问题,现有分析方法可以给出大时间范围中升力系数随时间的演化曲线。在初始时刻,可压缩与不可压缩却存在本质区别,前者由小扰动波主导,后者由环量主导。

2)对于大迎角突然启动问题,初始时刻的升力无论对于可压缩还是不可压缩,都存在突然下降现象,但对于大时间范围,不可压缩流动存在升力脉动现象,对于高马赫数可压缩流动,脉动现象明显减弱甚至消失。

3)对于大迎角可压缩问题,尚无理论分析方法可以给出长时间升力演化预测。一个针对高超声速条件的计算表明,大迎角下可能存在特殊的初始升力脉动现象。这一现象过去未见报道。

本文综述结果对从事气动弹性、扑翼飞行和大迎角机动研究具有借鉴作用。同时指出了存在的理论空白,包括大迎角可压缩问题的理论方法尚未建立,以及高超声速条件下存在一些升力系数脉动现象。这些问题需要进一步研究。

[1] Anderson J.McGraw-Hill series in aeronautical and aerospace engineering[M].[s.l.]:McGraw-Hill,1989.

[2] Sun M.Insect flight dynamics:stability and control[J].Reviews of Modern Physics,2014,86(2):615.

[3] Wagner H.Über die Entstehung des dynamischen auftriebes von tragflügeln[J].ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik,1925,5(1):17-35.

[4] Walker P B.Experiments on the growth of circulation about a wing and an apparatus for measuring fluid motion[J].Rep.Memo.Aeronaut.Res.(Great Britain),1931,1402.

[5] Pullin D I.The large-scale structure of unsteady self-similar rolled-up vortex sheets[J].Journal of Fluid Mechanics,1978,88(3):401-430.

[6] Graham J M R.The lift on an aerofoil in starting flow[J].Journal of Fluid Mechanics,1983,133:413-425.

[7] Pitt Ford C W,Babinsky H.Lift and the leading-edge vortex[J].Journal of Fluid Mechanics,2013,720:280-313.

[8] Dickinson M H,Gotz K G.Unsteady aerodynamic performance of model wings at low Reynolds numbers[J].The Journal of Experimental Biology,1993,174(1):45-64.

[9] Xia X,Mohseni K.Lift evaluation of a two-dimensional pitching flat plate[J].Physics of Fluids(1994-present),2013,25(9):091901.

[10] Pullin D I,Wang Z.Unsteady forces on an accelerating plate and application to hovering insect flight[J].Journal of Fluid Mechanics,2004,509:1-21.

[11] Li J,Wu Z N.Unsteadylift for the wagner problem in the presence of additional leading/trailing edge vortices[J].Journal of Fluid Mechanics,2015,769:182-217.

[12] Ashley H,Zartarian G.Piston theory-a new aerodynamic tool for the aeroelastician[J].Journal of the Aeronautical Sciences(Institute of the Aeronautical Sciences),1956,23(12):1109-1118.

[13] Liu D D,Yao Z X,Sarhaddi D,et al.From piston theory to a unified hypersonic-supersonic lifting surface method[J].Journal of Aircraft,1997,34(3):304-312.

[14] Oppenheimer M W,Skujins T,Bolender M A,et al.A flexible hypersonic vehicle model developed with piston theory,AIAA-2007-6396[R].Reston:AIAA,2007.

[15] Lomax H,Heaslet M A,Fuller F B,et al.Two-and three-dimensional unsteady lift problems in high-speed flight,NAGA 1077[R].Washington,D.C.:NACA,1952.

[16] Leishman J G.Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow[J].Journal of Aircraft,1988,25(10):914-922.

[17] Leishman J G.Indicial lift approximations for two-dimensional subsonic flow as obtained from oscillatory measurements[J].Journal of Aircraft,1993,30(3):340-351.

[18] Leishman J G.Unsteady lift of a flapped airfoil by indicial concepts[J].Journal of Aircraft,1994,31(2):288-297.

[19] Hariharan N,Leishman J G.Unsteady aerodynamics of a flapped airfoil in subsonic flow by indicial concepts[J].Journal of Aircraft,1996,33(5):855-868.

[20] Sitaraman J,Baeder J D.Computational-fluid-dynamicsbased enhanced indicial aerodynamic models[J].Journal of Aircraft,2004,41(4):798-810.

[21] Jose A I,Leishman J G,Baeder J D.Unsteady aerodynamic modeling with time-varying free-stream mach numbers[J].Journal of The American Helicopter Society,2006,51(4):299-318.

[22] Wu Z N,Bai C Y,Li J,et al.Analysis of flow characteristics for hypersonic vehicle[J].Acta Aeronautica et Astronautica Sinica,2015,36(1):58-85(in Chinese).吴子牛,白晨媛,李娟,等.高超声速飞行器流动特征分析[J].航空学报,2015,36(1):58-85.

[23] Bai C Y,Li J,Wu Z N.Generalized Kutta-Joukowski theorem for multi-vortex and multi-airfoil flow with vortex production—A general model[J].Chinese Journal of Aeronautics,2014,27(5):1037-1050.

[24] Li J,Wu Z N.A two-dimensional multibody integral approach for forces in inviscid flow with free vortices and vortex production[J].Journal of Fluids Engineering,2015,137(021205-1).

[25] Bai C Y,Wu Z N.Generalized Kutta-Joukowski theorem for multi-vortices and multi-airfoil flow(alumped vortex model)[J].Chinese Journal of Aeronautics,2014,27(1):34-39.

[26] Bai C Y,Li J,Wu Z N.Unsteady lift for impulsively started transonic/supersonic flow[C]//Proceedings of The ASME 2015 International Mechanical Engineering Congress&Exposition.to appear in,2015.

[27] Li J,Bai C Y,Wu Z N.Unsteady lift for the wagner problem of starting flow at large angle of attack[C]//Proceedings of The ASME 2015 International Mechanical Engineering Congress&Exposition.to appear in,2015.

[28] Gaunaa M,Bergami L,Heinz J.Indicial response function for finite-thickness airfoils,a semi-empirical approach,AIAA-2011-0542[R].Reston:AIAA,2011.

[29] Bisplinghoff R L,Ashley H,Halfman R L.Aeroelasticity[M].[s.l.]:Dover Publications,Inc,1996.