杨 帅

(中国矿业大学(北京)理学院，北京100083)

0 引 言

近年来，随着分数阶微分方程模型广泛建立于分数物理学、粘弹性力学、自动控制、生物化学、流体力学、随机过程等诸多应用科学领域［1］，分数阶微分方程理论引起了许多科研人员的浓厚兴趣和积极关注.关于分数阶微分方程解的存在性及其求解也取得了丰硕的成果［2～5］.分数阶微分方程初值问题是非线性微分方程的一个重要研究课题［6～9］.Diethelm［3］讨论了如下一类分数阶微分方程边值问题

本文同样讨论上述方程，遵循Diethelm 的核心证明思想，但将其假设条件弱化，应用Schauder 不动点定理证明这类分数阶微分初值问题解的存在性.

1 预备知识

定理1.1 设n ＞0，n ∉N，且m=［n］.更设K ＞0，h*＞0，b1，b2，…，bm∈R.定义

G= (x，y)∈R2:0 ≤x ≤h*，y ∈R时{ ，

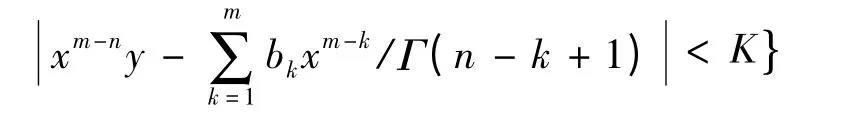
假定f:G →R 在G 上连续有界，并且关于第二个变量满足Lipschitz 条件，即∃L ＞0，s.t.∀(x，y1)，(x，y2)∈G，有

定理1.2 在定理1.1 的假设条件下，设h ＞0.y ∈C(0，h］是(1)的一个解当且仅当它是Volterra 积分方程

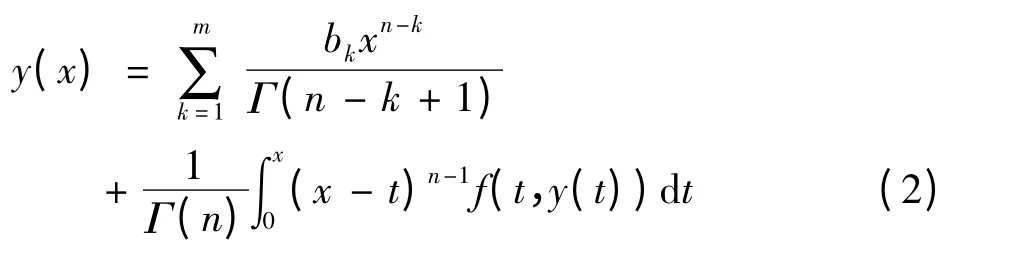
的一个解.

定理1.1 和定理1.2 分别引自Diethelm［3］定理5.1 和引理5.2.Diethelm 关于(1)或(2)解的存在性证明见Diethelm［3］引理5.3.

2 主要结果

定理2.1 在定理1.1 中将假定f 关于第二个变量满足Lipschitz 条件去掉后，定理结论依然成立.也就是说，即使f 关于第二个变量不满足Lipschitz 条件，(1)仍然有连续解y ∈C(0，h］.

证明: 由定理1.2 的证明过程知，将假定f 关于第二个变量满足Lipschitz 条件去掉后，(1)与(2)依然等价.

(i)，显然‖y‖^B≥0，且‖y‖^B=0⇔y=0.

(ii)∀y1，y2∈^B，，有

(iii)∀α ∈R，有

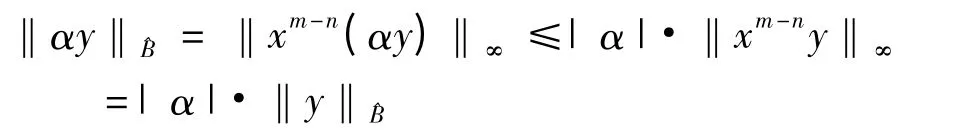
接下来，定义集合

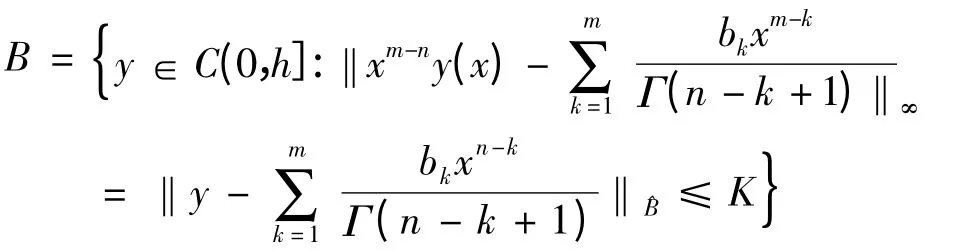
证明B 的凸性.∀α ∈R，满足0 ≤α ≤1，∀y1，y2∈B，有

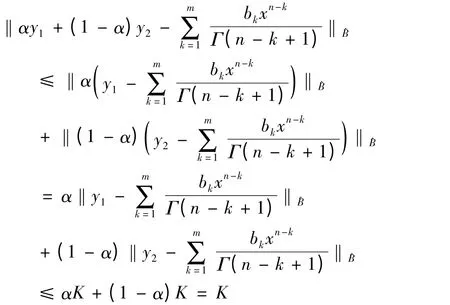
现在，在B 上定义算子F:

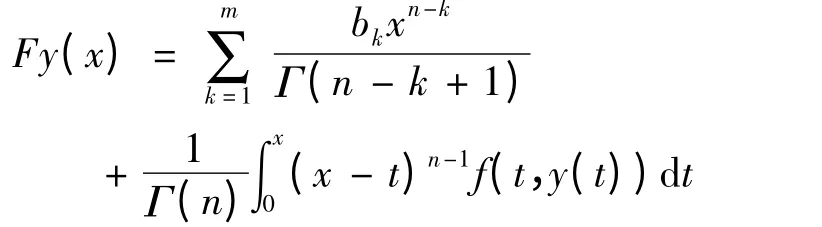
则求解Volterra 积分方程(2)转化为求算子的不动点问题.

事实上，

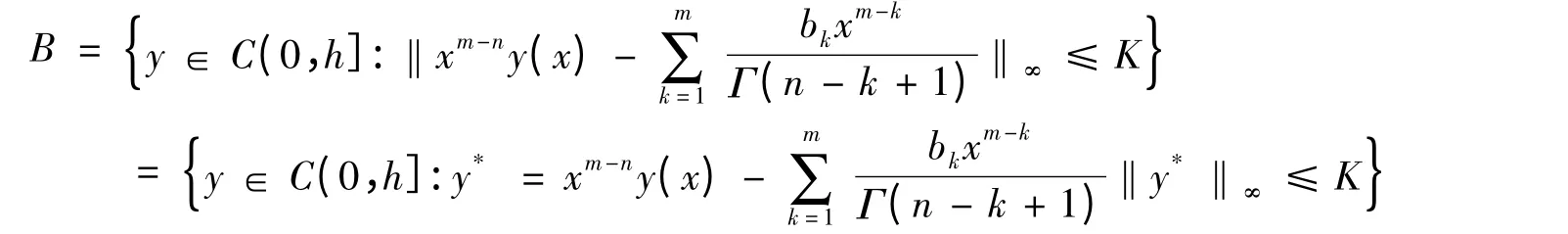
则算子F 的不动点问题又可以转化为这样一个算子H:B →B.

的不动点问题.

分以下几步来证明:

第一步，由

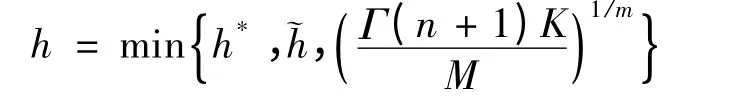
知，

取∀y ∈B，可以得到

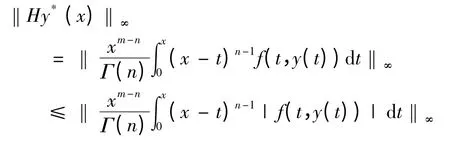
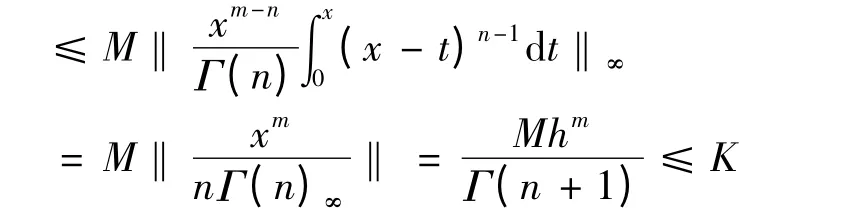
即Hy*(x)∈B，于是算子H:B →B.且可以得到Hy*(x)一致有界.

第二步，来讨论算子H 的连续性.∀y1∀y2∈B，x ∈(0，h］，看到，对于∀ε ＞0，由f 在‖y*‖∞≤K 上的一致连续性知，∃δ0＞0 使得当|y1－y2|＜δ0时，有

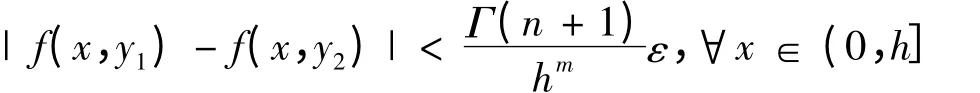
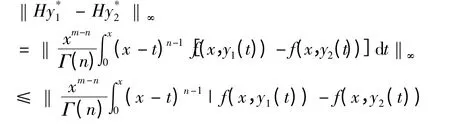
则H:B →B 连续.

第三步，∀y ∈B，∀x1，x2∈(0，h］，不妨设0＜x1≤x2≤h.对于∀ε ＞0，讨论

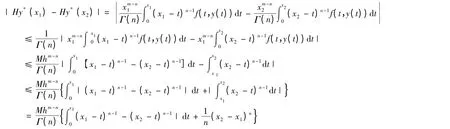
因为n ＞0，n ∉N，所以

(I)当n ＞1 时，

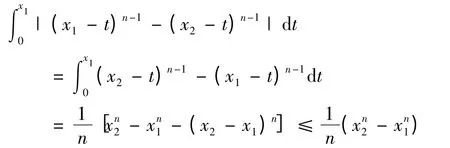
则假定此时存在|x2－x1|＜δ1，有

那么

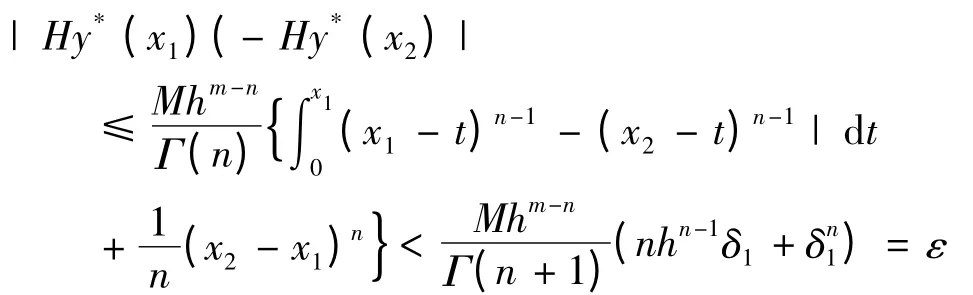
即δ1=δ1(ε).

(II)当n ＜1 时，有

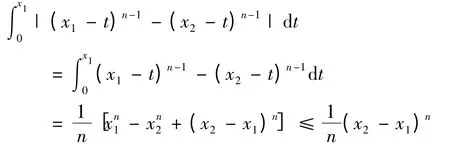
此时假定存在|x2－x1|＜δ2，则

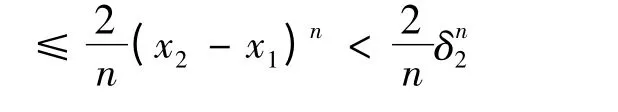
那么可以推出

即δ2=δ2(ε).

由(I)、(II)，取δ=min{δ1(ε)，δ2(ε)}，则当|x2－x1|＜δ 时，|Hy*(x1)－Hy*(x2)|＜ε.则Hy*等度连续.

由Ascoli－Arzela 定理知Hy*是B 中的相对紧集.因此H:B →B 全连续.根据Schauder 不动点定理知H 在B 中必有不动点.

综上，证明了分数阶微分初值问题(1)解的存在性，即(1)必有连续解y ∈C(0，h］.

［1］ J.Sabatier，O.P.Agrawal，J.A.Tenreiro Machado.Advances in Fractional Calculus［M］.Nether－Lands:Springer，2007.

［2］ A.A.Kilbas，H.M.Srivastava，J.J.Trujillo.Theory and Applications of Fractional Differential Equations［M］.Amsterdam:Elsevier，2006.

［3］ Kai Diethelm.The Analysis of Fractional Differential Equations［M］.Heidelberg:Springer，2010.

［4］ Kenneth S.Miller，Bertram Ross.An Introduction to the Fractional Calculus and Fractional Differential Equations［M］.New York:Wiley，1993.

［5］ Igor Podlubny.Fractional Differential Equations［M］.London:Academic Press，1999.

［6］ Shuqin Zhang.Positive Solutions to Singular Boundary Value Problem for Nonlinear Fractional Differential Equation［J］.Computers and Mathematics with Applications，2009，593.

［7］ Shuqin Zhang.Positive Solution of Singular Boundary Value Problem for Nonlinear Fractional Differential Equation with Nonlinearity That Changes Sign［J］.Positivity，2012，161.

［8］ Xinwei Su.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations［J］.Appl.Math.Lett.，2009，22.

［9］ Xinwei Su.Positive Solutions to Singular Boundary Value Problems for Fractional Functional Differential Equations with Changing Sign Nonlinearity［J］.Computers and Mathematics with Applications，2012，6410.

［10］ Emmanuele DiBenedetto.Real Analysis［M］.Heidelberg:Springer，2002.