杨树伟，王连堂，巩星田

(1.西北大学 数学学院，陕西 西安 710127；2.湘潭大学 数学系，湖南 湘潭 411105)



·数理科学·

基于Kress变换的开弧问题数值解

杨树伟1，王连堂1，巩星田2

(1.西北大学 数学学院，陕西 西安 710127；2.湘潭大学 数学系，湖南 湘潭 411105)

关于Helmholtz方程开弧问题，首先通过位势理论将其转化为边界积分方程问题，然后采用Kress变换将其化为近似闭区域上的问题。最后给出远场模式的数值解以检验数值方法的有效性和可行性。

Helmholtz方程；Kress变换；Dirichlet边界

关于Helmholtz方程开弧问题，因为涉及到开弧边界的特殊性，因而其具有一些与一般封闭曲线所不同的性质，自从文献[1]的作者做出Helmholtz方程开弧问题的论文之后，随后有文献[2-3]，而文献[1-3]都是运用一个余弦变换将开弧问题转化为闭区域上的问题来解决，本文作者尝试用另外一种办法来求解Helmholtz方程开弧问题，即文献[4]中用于求解Laplace方程有角闭区域的办法，因为它实质上是通过一个变量替换，在最后数值求积的时候采用分级网格办法来代替一般的等距网格办法，从而提高数值收敛率，但此办法不能简单的从Laplace方程推广到Helmholtz方程，因为涉及到Helmholtz方程基础解的复杂性，我们再按照文献[5]中对单层位势的特殊分解方法，将得到的第一类算子方程的核进行对数奇性分离，以便最后数值求积的时候利用权积分可以得到数值解，为此下面先简要介绍一下Kress变换。

1 Kress变换

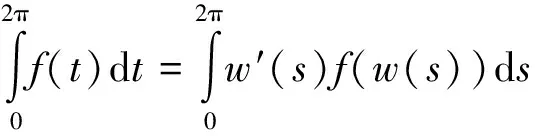
(1)

对上式运用梯形公式得

(2)

权函数和网格点由下式给出

取函数w(s)为[4]

(3)

0≤s≤2π。

这里p≥2，注意到三次多项式的选取使得v(0)=0,v(2π)=1，以及w′(π)=2。

2 边界积分方程

考虑均匀介质中传播的声波，此声波碰到一个无限长柱体，柱体截面D⊂R2，母线平行于z轴，入射波为平面波，此声波碰到柱体后发生散射，在数学上此类问题可归结为Helmholtz方程外边值问题来解决。

Δu+k2u=0,inR2Γ，k>0

(4)

满足Dirichlet边界条件

u=0, onΓ

(5)

而全场u∈C2(R2Γ)∩C(R2)可以分解为u=ui+us入射场ui=eikx·d,|d|=1和未知散射场us，散射场必须满足如下的Sommerfeld辐射条件

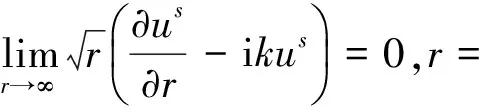
(6)

在所有方向上一致成立。

在对未知函数重新命名之后，上面的正散射问题可约化为下列开弧边界的外Dirichle问题：给定函数f∈C(Γ)，找出Helmholtz方程的一个解u∈C2(R2Γ)∩C(R2)

Δu+k2u=0，inR2Γ，k>0

(7)

其满足边界条件

u=f,onΓ

(8)

以及Sommerfeld辐射条件。

定理1[1]开弧边界上的外Dirichlet问题至多有一解。

通过寻求如下单层位势形式的解来建立问题(6)～(8)解的存在性，因为任何一个Helmholtz方程的解均可表示为单，双层位势形式的组合。

(9)

这里Φ(x,y)为二维情形下Helmholtz方程基础解

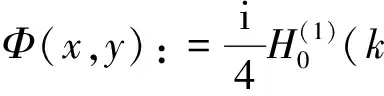
(10)

x∈Γ{z1}∪{z-1}。

(11)

(12)

假定边界曲线是C3类弧线，即

Γ={x(t):t∈[0,2π]}。

这里x:[0,2π]→R2为一单值三次连续可微函数。

对式(12)参数化得

(13)

其中

(14)

Ψ(t):=φ(x(t))|x′(t)|，

g(t):=-2f(x(t))，

r(t,τ):=|x(t)-x(τ)|，

令t=w(s)，式(13)变为

0≤s≤2π，

(15)

其中φ(σ)=Ψ(w(σ))w′(σ)。

3 核的对数奇性分离

(16)

(17)

从Hankel函数的定义以及零阶Neumann函数的级数表达式(17)，可将核K(w(s),w(σ))裂解为如下形式[5]。

(18)

其中

(19)

K2(s,σ)=K(w(s),w(σ))-

(20)

均是解析的，K2(s,σ)为剩余无奇性的全体。再次利用级数表达式(16)和式(17)，可以得到其对角项。

K1(s,s)=-k2[w′(s)x′(w(s))]2，

(21)

K2(s,s)=

(22)

4 数值积分办法

(23)

(24)

事实上上面这两个数值求积公式是将f(τ)用它的三角插值多项式来代替，然后积分得到，插值时基函数取为Lagrange三角插值基，详细可参看文献[6]。其中

(25)

(26)

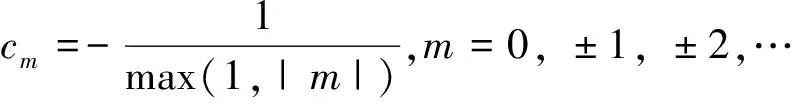
对方程式(15)以及相应的核分解式(18)，运用数值积分公式(2)，(23)，(24)得

(27)

我们注意到这里下标改从j=1开始，这是因为φ(0)=0的缘故。为了得到方程的近似解，将其投影到有限维的子空间上，利用配置法得

i=1,…,2n-1。

(28)

图1 开弧边界Fig.1 The boundary of open arc

对于数值算例，为了和文献[1]中的例子做一比较，取入射平面波为ui(x)=eikx·d，指数p=8，开弧边界为

用上面所叙述的散值积分公式求解出式(15)的密度函数以后，再用式(2)求解式(28)，表1给出了远场模式的一些逼近值，这里取入射波的方向为d=(1,0)。注意到表1中的数据按指数级收敛，同时收敛速度明显高于文献[1]中的数据。对于以上方法的收敛性分析可参看相关文献[6-8]。

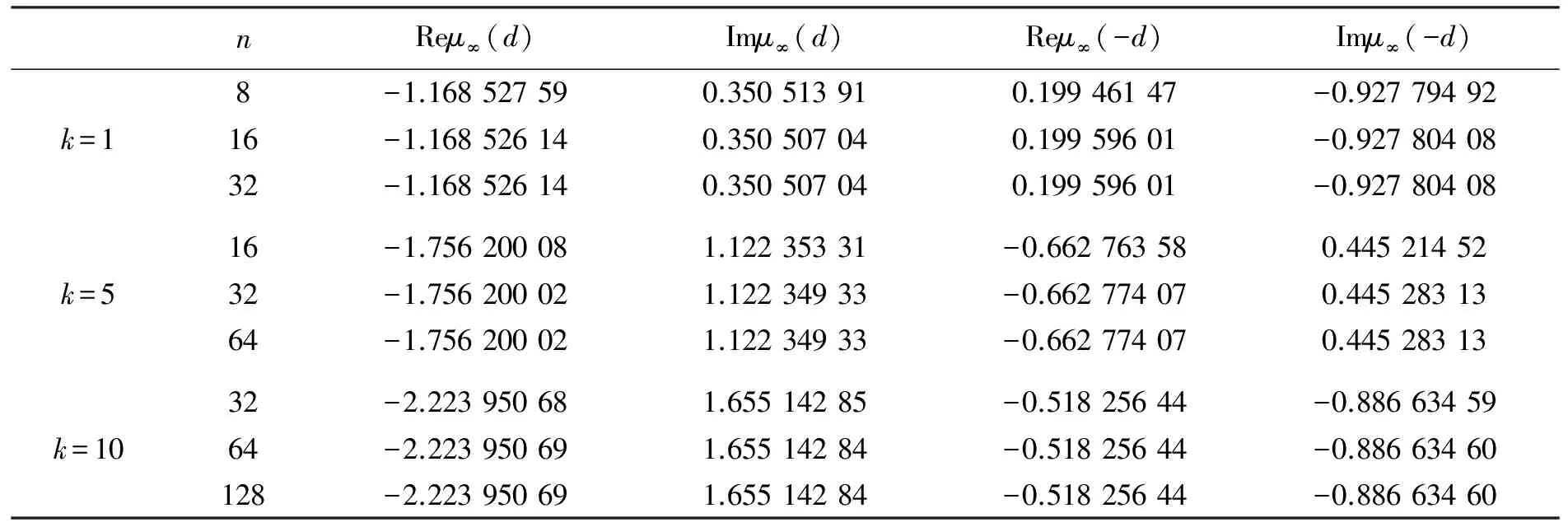
表1 远场模式数值解Tab.1 Numerical results for the far-field pattern

[1] KRESS R.Inverse scattering from an open arc[J].Math Methods Appl Sci,1995,18:267-293.

[2] MONCH L.On the numerical solution of the direct scattering problem for a sound-hard openarc[J].Comput Appl Math,1996,71:343-356.

[3] KRESS R.Lee Kuo-ming.Integral equation methods for scattering from an impedance crack[J].Comput Appl Math,2003,161:161-177.

[4] KRESS R.A nystrom method for boundary integral equation in domains with corners[J].Numer Math,1990,58:145-161

[5] KRESS R.SLOAN L H. On the numerical solution of a logarithmic integral equation of the first kind for the Helmholtz equation[J].Numer Math,1993,66:199-214.

[6] KRESS R.Linear Integral Equations[M].Berlin:Spring-Verlag,1989.

[7] COLTON D,KRESS R.Inverse Acoustic and Electromagnetic Scattering Theory [M].Berlin:Spring-Verlag,1992.

[8] COLTON D,KRESS R.Integral Equation Methods in Scattering Theory[M].New York:Wiley-Interscience Publication,1983.

(编 辑亢小玉)

On the numerical solution of open arc problem based on the Kress transformation

YANG Shu-wei1, WANG Lian-tang1,GONG Xing-tian2

(1.School of Mathematics, Northwest University, Xi′an 710127，China; 2.School of Mathematics, Xiangtan University, Xiangtan 411105, China)

The paper is on the open arc boundary problem of Helmholtz equation.Reduce it into boundary integral equation problem by potential theory, then using Kress transformation, the problem which is closely related to the integral equation for the case of a closed boundary is obtained.And numerical results of far-field pattern are presented to test the applicability and the effectiveness of the method.

Helmholtz equation; Kress transformation; Dirichlet boundary

2014-09-15

国家自然科学基金资助项目(11401144)

杨树伟，男，甘肃定西人，从事数学物理方程反问题研究。

O241.8

：ADOI：10.16152/j.cnki.xdxbzr.2015-03-005