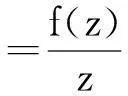一类Möbius不变空间的无导数特征

2015-02-19韩金桩周继振

安徽大学学报（自然科学版） 2015年2期

关键词：延安大学呼伦贝尔理工大学

韩金桩,周继振

(1.呼伦贝尔学院数学科学学院,内蒙古呼伦贝尔　021008;2.安徽理工大学理学院,安徽淮南　232001)

一类Möbius不变空间的无导数特征

韩金桩1,周继振2

(1.呼伦贝尔学院数学科学学院,内蒙古呼伦贝尔021008;2.安徽理工大学理学院,安徽淮南232001)

摘要:通过运用Bergman度量,获得了一类bius不变的函数空间,即QK(p,p-2)空间的几个等价的无导数刻画,包括双重积分特征、振荡、平均振荡和p-平均振荡刻画. 这些特征是QK(p,p-2)空间重要的分析性质,它进一步完善了QK(p,p-2)空间理论,有重要的理论和应用意义.

关键词:QK(p,p-2)空间;双重积分; Bergman 度量;p-平均振荡

Foundation item:Support by Department of Education Funded Projects of Inner Mongolia (NJZY14305);Department of Education Funded Projects of Anhui Province(KJ2013A101)

Author’s brief:HAN Jin-zhuang(1961-), male, born in Hulunbeier of Inner Mongolia, associate professor of Hulunbeier University.

0Introduction

Throughout this paper, the unit disc is denoted by D. For any given a∈D, let

where dλ(z)=(1-|z|2)-2dA(z). Note that dA(z) is the Eculidean area measure on D so that A(D)=1. Equipped with the norm ‖f‖=|f(0)|+‖f‖K,p, the space QK(p,p-2) is a Banach space when p≥1. We know that the space QK(p,p-2) is a subset of the Bloch space[1]. The basic properties of QK(p,p-2) spaces can be founded in [1]. If p=2,then QK(p,p-2) spaces are just QKspaces[2-3]. If K(0)>0 and p>2, then the space QK(p,p-2) coincides with the analytic Besov space.

It is clear that the space QK(p,p-2) is Mobius invariant, i.e., ‖f∘φa‖K,p=‖f‖K,p. The space QK(p,p-2) is nontrivial if and only if it contains all polynomials[4], that is

(1)

Making a change of variables in the above integral and simplifying the result using polar coordinates, we obtain that the space QK(p,p-2) is nontrivial if and only if

In the paper，we may need two conditions onKas follows

(2)

and

(3)

where

The derivative-free characterizations of QKspaces have been study in many papers[4-5]. In this paper, we study the derivative-free characterization in QK(p,p-2) spaces by applying the Bergman metric andp-mean oscillation. The technique is suggested by the theory of Bergman space. The result is important which enriches the theory of QKtype spaces. It has important significance in application.

Furthermore, we suppose that the nondecreasing function K satisfies K(2t)≈K(t)，that is, K(2t)K(t)K(2t). Note, K(2t)K(t) means that there exists a constant C (independent oft),such that

K(2t)≤CK(t).

1Derivative-Free characterizations of QK(p,p-2) spaces

In this section, we give some derivative-free characterizations of QK(p,p-2) spaces. We now introduce some basic definitions.

Recall that the Bergman metric of D is given by

For any z∈D and r>0, the pseudo-hyperbolic disc is defined by

The pseudo-hyperbolic disc D(z,r) is an Euclidean disc[5]. Let |D(z,r)| be the Euclidean area of D(z,r).Obviousy, |D(z,r)|≈(1-|z|2)2aszapproaches the unit circle for any given r>0. It is well known that

(4)

Iffis an analytic function onD, we define the oscillation offatzin the Bergman metric as

Thep-mean oscillation offatzin the Bergman metric is defined by

where

and p>0. If p=2, we call it the mean oscillation offat z in the Bergman metric. See section 7.1 of [6]. Furthermore, we define

for p,r>0.

The following result will be needed in the proof of the main theorem.

Lemma 1[7]LetKsatisfy the condition (3). For any given z∈D, then

Lemma 2[8]Let 0

Lemma 3Let K satisfy the condition (3) and 0

if and only if

ProofBy Lemma 2, we have

Note that

Make a change of variables, Then

Given a fixed r>0, then

(5)

for all w∈D(z,r). Proposition 4.3.8 of [6] and (4) imply

On the other hand, by Fubini’s Theorem，we have

Lemma 1Gives

The proof is complete.

Theorem 1Let K satisfy the condition (3). If r>0, 0

(1) The functionfbelongs to QK(p,p-2) spaces.

ProofWe make two change variables u=φa(z) and v=φa(w). Then

Lemma 3 implies

Take the supremum overa∈Dboth side. This shows (1)⟺(2).

By Proposition 4.3.8 of [6]，we have the following inequality

Replacingfby f-f(z), then

(6)

for all analyticsfandz, w∈D. This means

when w∈D(z,r).If w∈D(z,r), then D(w,r)⊂D(z,2r) and |D(z,2r)|≈|D(w,r)|. By (5) we have

This gives

We have showed (2) ⟹ (3). If w,u∈D(z,r), then

So we have

This gives

Then we obtain

This shows (3)⟹(4).

We apply (6) to get the following inequality

This proves (4)⟹(5).

Replacingfby f∘φz-f(z), we obtain

Making a change of variables, we have

So (5) implies (1). The proof is complete.

Denote by ∂D the unit circle. For a subarc I⊂∂D, let θ be the midpoint ofIand denote

where |I| denotes the length of I. If |I|>1, we set S(I)=D. S(I) is called the Carleson box. A positive measuredμ is said to be a K-Carleson measure onDprovided

If K satisfies the conditions (2) and (3), then dμ is aK-Carleson measure if and only if

by Theorem 3.1 of [3]. By Theorem 1, we have the following result.

Corollary 1Let K satisfy the conditions (2) and (3). If r>0, 0

(1) The functionfbelongs to QK(p,p-2) spaces.

(3) (ωr(f)(z))pdλ(z) is aK-Carleson measure.

(4) (MOp,r(f)(z))pdλ(z) is aK-Carleson measure.

(5) (Op,r(f)(z))pdλ(z) is aK-Carleson measure.

2Derivative-Free characterizations of QK,0(p,p-2) spaces

For 0

A positive measuredμ is said to be a vanishingK-Carleson measure on D provided

If K satisfies the conditions (2) and (3), thendμ is a vanishingK-Carleson meansure if and only if

by Theorem 3.1 of [3].

Carefully checking the proof of Theorem 1 and Corollary 1. We see that the little version of Theorem 1 and Corollary 1 hold as well, from which we obtain the following results.

Theorem 2Let K satisfy the condition (3). If r>0, 0

(1) The functionfbelongs to QK,0(p,p-2) spaces.

Corollary 2Let K satisfy the conditions (2) and (3). If r>0, 0

(1) The functionfbelongs to QK,0(p,p-2)spaces.

(3) (ωr(f)(z))pdλ(z) is a vanishingK-Carleson measure.

(4) (MOp,r(f)(z))pdλ(z) is a vanishingK-Carleson measure.

(5) (Op,r(f)(z))pdλ(z) is a vanishingK-Carleson measure.

We leave the details of Theorem 2 and Corollary 2 to the interested reader.

References:

[1]Wulan H,Zhou J Z.QKtype spaces of analytic functions[J].J Funct Spaces Appl,2006,4:73-84.

[2]Essen M,Wulan H.On analytic and meromorphic functions and spaces ofQKtype[J].Illinois J Math,2002,46:1233-1258.