李 阳，齐淑华，丁淑妍

(大连民族学院 理学院，辽宁 大连116605)

近年来，半定规划问题(SDP)因其应用范围十分广泛而成为优化领域的一个新的研究热点。人们注意到它可以用来解决组合优化、最优控制、统计学、金融学、工程信号处理、交通管理等很多实际问题［1-2］。于是，研究能够有效解决半定规划问题的算法成为现实中生产生活的需要。

半定规划问题主要分为线性半定规划和非线性半定规划。对于线性半定规划算法的研究，目前的成果已经比较丰富了，而对于非线性半定规划问题，主要的求解算法是非线性拉格朗日函数方法。2003 年，Kocavra 和Stingl 在求解非线性半定规划问题的算法研究方面做了大量工作，给出了解决较大规模问题的一类修正障碍函数法并给出了数值程序PENNON［3］。2006 年，Stingl 在他的博士论文中给出了一类非线性拉格朗日函数法［4］，这项工作为后续研究奠定了坚实的基础。随后，Noll 在2007 年给出了一个求解非线性半定规划问题的具有局部收敛性的增广拉格朗日函数法［5］，提出了wedge 收敛的定义，并从新的角度给出了收敛定理证明。另外，Sun，Sun 和Zhang 在2008 年还研究了当严格互补条件不成立时的求解非线性半定规划问题的增广拉格朗日函数法的收敛速度［6］，在算法理论研究上取得了突破。2013 年，Zhang，Li 和Wu 在文献［7］中给出了一类求解非凸半定规划问题的非线性拉格朗日函数法的框架，这是一项相对完整的工作，但是该文献并没有证明与构成非线性拉格朗日函数的Löwner算子相关的4 种具体的实值函数是如何满足假设条件的，而这些结论在某种程度上并不是显然的。

本文根据一阶均差矩阵的定义以及4 种实值函数的特有性质，就上述问题给出详尽的证明过程，对文献［7］进行了必要的补充。

1 预备知识

文献［7］研究了具有如下形式的非凸半定规划问题:

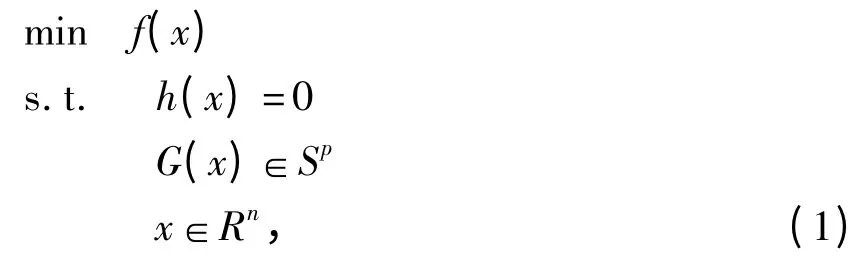
式中，f:Rn→R，h:Rn→Rq，G:Rn→Sp都是二次连续可微的，Sp是p ×p 维实对称矩阵构成的空间;并构造了形式如下的一类非线性拉格朗日函数:

这里t ＞0 是一个惩罚参数，在数值试验取值时，t往往是一个很小的数。‖·‖ 代表Frobenius 范数，〈A，B〉表示矩阵A 和B 的内积，Φ 是Löwner算子，且

在这里，diag(μi)，i=1，2，…p 表示以μi为对角线元素构成的对角阵，对G(x)做谱分解得

文献［7］中构成Löwner 算子的实值函数φ:R→R 要满足的3 个假设条件如下:

(A1)φ 在(-∞，ω0)上是严格凸的，严格单调递增的二次连续可微函数，这里ω0＞0 是一个常数;

(A2)φ(0)=0，φ'(0)=1 并且φ″(0)＞0;

(A3)对于任意固定的ω ＞0，任取λ，λk，λl∈(-∞，-ω］，有|t-1φ［1］(0，t-1λ)|≤c1(ω，λ)，且|t-1φ［1］(t-1λk，t-1λl)|≤c2(ω，λk，λl)，这里c1(ω，λ)和c2(ω，λk，λl)是分别与(ω，λ)和(ω，λk，λl)相关的正数。

同时文献［7］给出了4 种实值函数满足上述假设条件，分别为修正的Carroll’s 函数φMC(t)=(1 -t)-1-1、修正的指数函数φME(t)=et-1、Log-Sigmoid 函数φLS(t)=2(lg(1 +et)-lg2)与函数φ1(t)=2lg((1 -t)-1+1)-2lg2。这些实值函数在研究求解经典的非线性规划的非线性拉格朗日方法时，常常被用来构造非线性拉格朗日函数。

为了解释假设条件中φ［1］(λk，λl)的定义，我们给出定义。

定义1 实值函数φ 在λ∈Rp处的一阶均差矩阵记为φ［1］(λ)，它的第k 行第l 列的元素有如下定义:

2 问题的证明

下面分别证明这4 种函数满足假设条件(A1)—(A3)。

证明 (1)修正的Carroll’s 函数φMC(t)=(1 -t)-1-1。

在(-∞，1)上，显然φMC是二次连续可微的。φ″MC(t)=＞0，所以φMC是严格凸的。而且φ'MC=＞0 表明φMC是严格单调递增的。易验证φMC(0)=0，φ'MC(0)=1 和φ″MC(0)|t=0=t=0=2 ＞0。又因为对于任意固定的ω ＞0，任取λ，λk，λl∈(-∞，-ω］有

又因为φMC的有效域是(-∞，1)，所以t-1λ∈(-∞，1)，则可得

因此，φMC满足假设条件(A1)—(A3)，并且c1(ω，λ)=c2(ω，λk，λl)=ω-1。

(2)修正的指数函数φME(t)=et-1。

在(-∞，+∞)上，显然φME是二次连续可微的。φ″ME(t)=et＞0，所以φME是严格凸的。并且，φ'ME=et＞0 表明φME是严格单调递增的。易得φME(0)=0，φ'ME(0)|t=0=1 和φ″ME(0)|t=0=e0=1 ＞0。又因为对于任意的ω ＞0，任取λ，λk，λl∈(-∞，-ω］有

|t-1(0，t-1λ)|=|t-1(t-1λ，0)|=t-1|=|| ≤| λ-1| ≤ω-1。并且

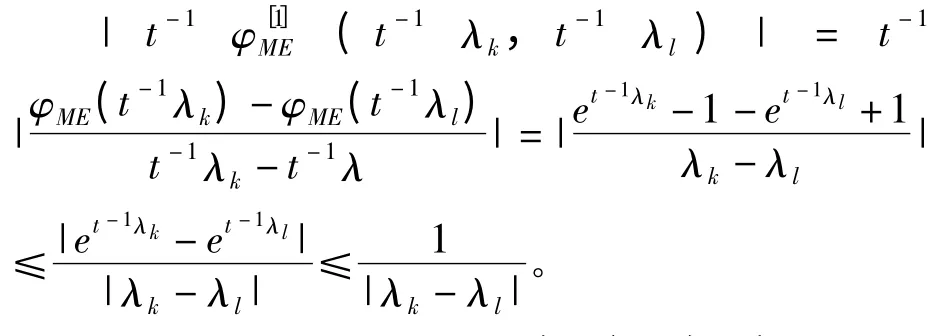
因此，φME满足假设条件(A1)—(A3)，并且c1(ω，λ)=ω-1，c2(ω，λk，λl)=1/|λk-λl|。

(3)Log-Sigmoid 函数φLS(t)=2(lg(1 +et)-lg2)。

在(-∞，+∞)上，显然φLS是二次连续可微的。φ″LS(t)=＞0，所以φLS(t)是严格凸的。φ'LS=2et(1 +et)-1＞0 说明φLS(t)在(-∞，+∞)上是严格单调递增的。易得φLS(0)=0，φ'LS(0)|t=0=2|t=0=1 和φ″LS(0)|t=0=2et(1+et)-1-2e2t(1 +et)-2|t=0=＞0。又因为对于任意固定的ω ＞0，任取λ，λk，λl∈(-∞，-ω］有

并且

因此，φLS满足假设条件(A1)—(A3)。并且c1(ω，λ)=2lg2ω-1，c2(ω，λk，λl)=。

(4)φ1(t)=2(lg (+1)-lg2)。

在(-∞，1.5)上，显然φ1是二次连续可微的且φ″1(t)=＞0，所以φ″1(t)是严格凸的。而且，φ'1=＞0，说明φ1是严格单调递增的，易得φ1(0)=0，φ'1(0)|t=0=2=1 和φ″1(0)|t=0=-=＞0。又因为对于任意固定的ω ＞0，任取λ，λk，λl∈(-∞，-ω］有

并且，

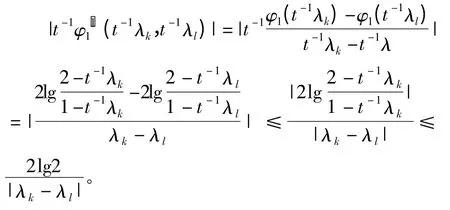
因此，φ1满足假设条件(A1)—(A3)，并且c1(ω，λ)=2lg2ω-1，c2(ω，λk，λl)=。

3 结 语

本文在文献［7］工作的基础上进行补充，借助实值函数一阶均差矩阵的定义，给出了4 种拉格朗日函数满足假设条件(A1)—(A3)的详细证明。当然，在求解非凸半定规划问题的算法方面还有很多值得关注的课题。例如，如何给出好的数值算法来求解实际中的非凸半定规划问题就是一个值得研究的课题，今后我们将致力于这方面的研究。

［1］BOUD S，GHAOUI EL L，FERON E，et al. Linear Matrix Inequalities in System and Control Theory ［M］.Philadelphis:Society for Industrial and Applied Mathematics，1994.

［2］JARRE F，WOLKWIEZ H，SAIGAL R. Handbook of Semidefinite Programming:Theory，Algorithm and Applications［M］. New York:Springer-Verlag，2000.

［3］KOCVARA M，STINGL M. PENNON—A code for convex nonlinear and semidefinite programming［J］. Optimization Methods and Software，2003，18:317 -333.

［4］STINGL M. On the solution of nonlinear semidenite programs by augmented lagrangian methods［D］. Aachen:Erlangen University，2006.

［5］NOLL D. Local convergence of an augmented Lagrangian method for matrix inequality constrained progrmming［J］. Optimization Methods and Software，2007，22:777 -802.

［6］SUN D，SUN J，ZHANG L. The rate of convergence of the augmented Lagrangian method for nonlinear semidenite programming［J］. Mathematical Programming，2008，114:349 -391.

［7］ZHANG L，LI Y，WU J. Nonlinear rescaling Lagrangians for nonconvex semidefinite programming［J］. Optimization. 2014，63:(6):899 -920..