王自强， 曹俊英

(贵州民族大学 理学院 贵州 贵阳 550025)



非线性Volterra积分方程组的一个高阶数值格式

王自强， 曹俊英

(贵州民族大学 理学院 贵州 贵阳 550025)

对非线性Volterra积分方程组构造了一个高阶数值格式.借助经典block-by-block方法，构造了一个所谓的修正block-by-block方法.方法除第1,2层外,每一步的解层与层之间都不需要耦合求解，并且保存了block-by-block方法好的收敛性.对此格式的收敛性进行了严格的分析，证明数值解逼近精确解的阶数是4阶.

非线性Volterra积分方程组； 高阶格式； 收敛性分析

0 引言

近年来，积分方程和非线性方程已经成为研究热点[1-2].考虑非线性Volterra积分方程组

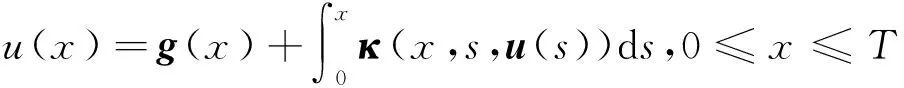
(1)

其中,u(x)=(u1(x),u2(x),…,un(x))T,g(x)=(g1(x),g2(x),…,gn(x))T,κ(x,s,u(s))=(κi,j(x,s,uj(s)))n×n.

关于式(1)的数值方法，学者们已经做了大量的研究.文[3]对积分方程提出了一种所谓的乘积型积分技巧，这是block-by-block思想的雏形.文[4]对非线性Volterra积分方程首次提出block-by-block方法.文[5]给出了求解线性Volterra积分方程一个通用的block-by-block方法.文[6]利用block-by-block方法求解了非线性Volterra积分方程组.文[7]利用block-by-block方法求解了非线性二维Volterra积分方程.文[8]把block-by-block方法应用到求解分数阶常微分方程问题中.文[9]证明了文[8]中的算法的收敛阶至少是3阶.文[10]提出了一种修正的block-by-block方法，并应用修正的block-by-block方法求解了非线性Volterra积分方程.本文利用文[10]修正的block-by-block方法求解非线性Volterra积分方程组，得到了一个高阶格式，可以单独来解未知量.这个方法的优势在于除了第1层和第2层外，其余的未知量不需要耦合求解，最后给出了收敛性分析.

1 高阶格式的构造

把式(1)写成分量形式的非线性Volterra积分方程组

(2)

其中，式(2)中的κi(x,s,u1(s),…,un(s))定义为

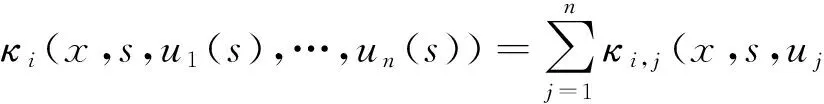
(3)

文[11]证明了式(2)存在唯一解的充要条件，因此假定方程组(2)有唯一解.下面推导高阶格式：将区间[0,T]分成2N个等分的子区间，其中h=T/2N, 设xj=jh,j=0,1,…,2N.式(2)在点xj上的数值解记为Ui,j.开始计算最初两步的解，首先确定ui(x),i=1,2,…,n，在x1上的值.利用式(3), 则得

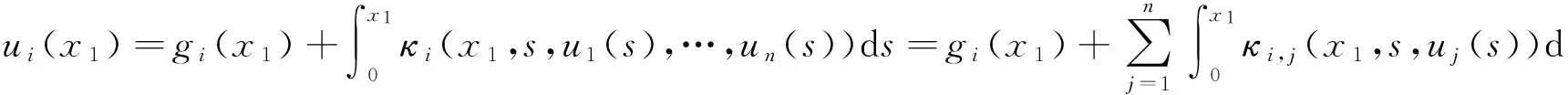
(4)

在积分区间[0,x1]上，对式(4)用Simpson公式进行近似求解,

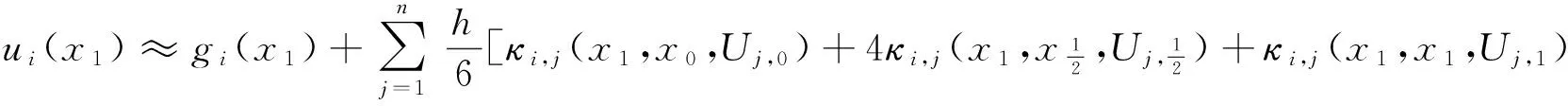
(5)

下面利用二次Lagrange插值来逼近半点项，

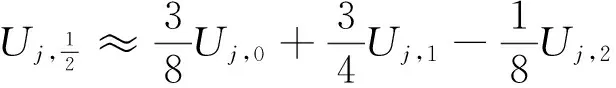
(6)

将式(6)代入式(5), 则得

κi,j(x1,x1,Uj,1)]，

(7)

其中,Uj,0=gj(x0). 注意到，用式(7)计算Ui,1需要Ui,2的值.

相似地，计算ui(x),i=1,2,…,n,在x2上的值，利用式(3), 得

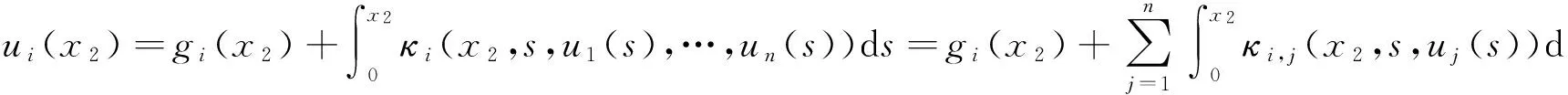
(8)

在积分区间[0,x2]上，对式(8)用Simpson公式进行近似求解,

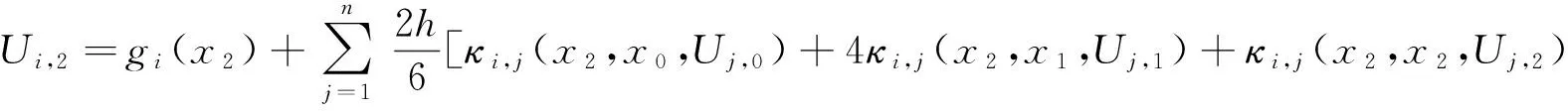
(9)

如上所述，在式(7)和(9)中,最初两步的解Ui,1和Ui,2是耦合的.因此，必须同时解出.

现在，构造下一步的格式.假设已经构造出Ui,j,i=1,2,…,n,j=0,1,…,2m,希望逼近ui(x2m+1),ui(x2m+2)按照同一个思路，有

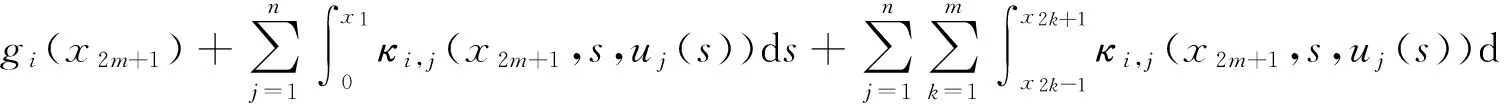
(10)

在积分区间[0,x1],[x2k-1,x2k+1]上，对式(10)用Simpson公式进行近似求解,

κi,j(x2m+1,x2k+1,Uj,2k+1)].

(11)

将式(6)代入(11), 即得

4κi,j(x2m+1,x2k,Uj,2k)+κi,j(x2m+1,x2k+1,Uj,2k+1)].

(12)

为了计算ui(x2m+2),i=1,2,…,n,使用下面的逼近，

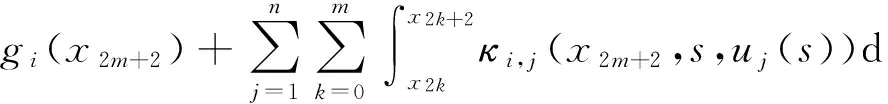
(13)

在区间[x2k,x2k+2]上， 对式(13)用Simpson公式进行近似求解，得

4κi,j(x2m+2,x2k+1,Uj,2k+1)+κi,j(x2m+2,x2k+2,Uj,2k+2)].

(14)

注1在标准的block-by-block中，如ui(x2m+1)不是用式(10)，而是用下面的离散形式来逼近,

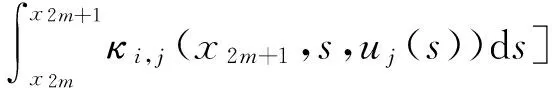
(15)

式(15)中最后一个积分是用点x2m,x2m+1,x2m+2上的二元二次插值来逼近的.因此，得到一个关于Ui,2m+1和Ui,2m+2的耦合系统.显然，对于所有的m=1,2,…,N-1,要想得到Ui,2m+1和Ui,2m+2,解式(10)比解耦合系统更加容易.

接下来，将给出上述格式(7), (9)和(12), (14)的收敛性分析.

2 收敛性分析

设κi,j(x,s,v)关于第3个变量满足Lipschitz条件：即存在一个常数L, 使得

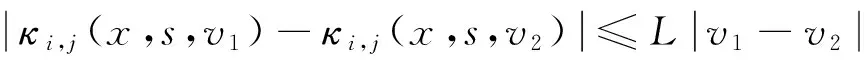
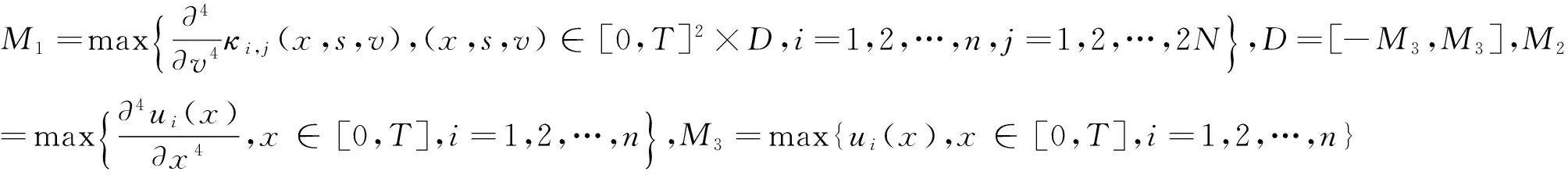
定理1由方程(2)所给出问题的数值格式(7) , (9)和(12), (14)是收敛的，且收敛阶为4阶.

证明记εi,j=Ui,j-ui(xj),i=1,2,…,n,j=0,1,…,2N,有

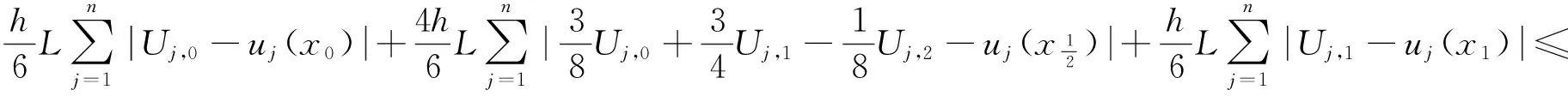
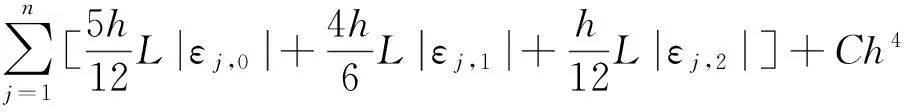
(16)

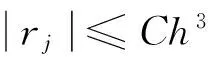
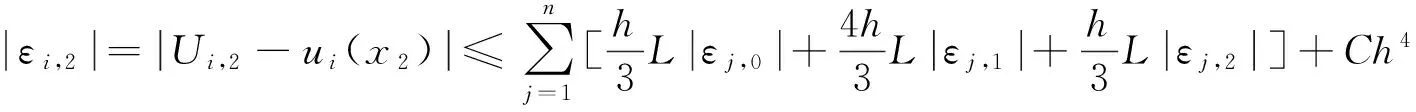
同样地，由式(12),得

(17)

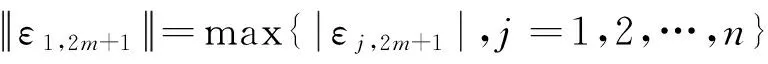
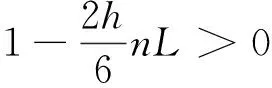
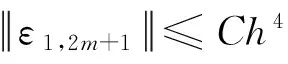
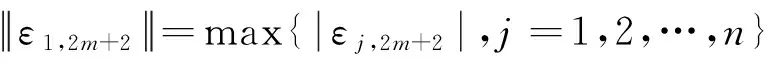
定理1证毕.

3 数值算例

应用本文提出的算法求解n=2时的非线性Volterra积分方程组.

例1考虑非线性Volterra积分方程组

它的精确解为u1(x)=cosx,u2(x)=sinx.

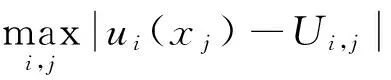
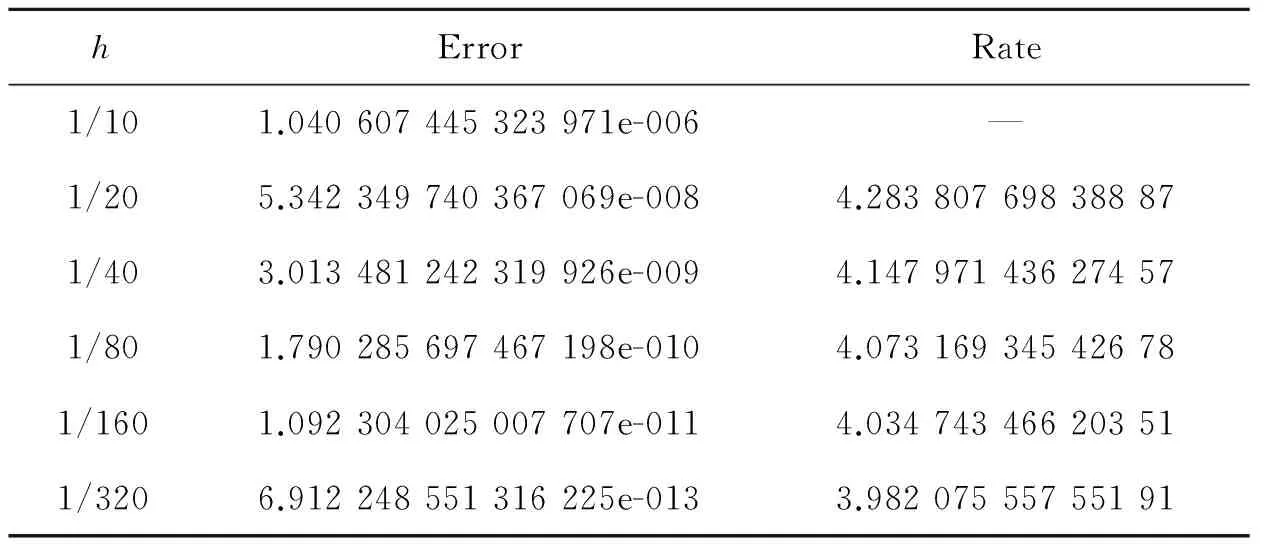
表1 最大误差随步长h的变化与收敛阶Tab.1 Maximum errors and decay rate with different h

[1] 杨军,葛艳芳,赵硕,等.一类分数阶积分方程解的存在性和吸引性[J]. 郑州大学学报：理学版,2013, 45(1):5-9.

[2] 石玉,陈宝凤,李威,等. 非线性抛物方程的一个新混合元格式的超收敛分析[J]. 信阳师范学院学报：自然科学版,2014,27(3): 328-331.

[3] Young A.The application of approximate product-integration to the numerical solution of integral equations[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences，1954, 224(1159):561-573.

[4] Linz P. A method for solving nonlinear Volterra integral equations of the second kind[J]. Math Comput， 1969, 23 (107):595-599.

[5] Nadjafi J S, Heidari M. A generalized block-by-block method for solving linear Volterra integral equations[J].Appl Math Comput, 2007, 188(2):1969-1974.

[6] Katani R, Shahmorad S. Block by block method for the systems of nonlinear Volterra integral equations[J].Applied Mathematical Modelling, 2010, 34(2):400-406.

[7] Mirzaee F, Rafei Z. The block by block method for the numerical solution of the nonlinear two-dimensional Volterra integral equations[J].Journal of King Saud University-Science, 2011, 23(2):191-195.

[8] Kumar P，Agrawal O P. An approximate method for numerical solution of fractional differential equations[J].Signal Process, 2006, 86(10):2602-2610.

[9] Huang J, Tang Y，V′azquez L. Convergence analysis of a block-by-block method for fractional differential equations[J].Numer Math Theor Meth Appl, 2012, 5(2):229-241.

[10]Cao J, Xu C. A high order schema for the numerical solution of the fractional ordinary differential equations[J]. Journal of Computational Physics, 2013, 238(1):154-168.

[11]Burton T A. Volterra Integral and Differential Equations[M]. New York：Elsevier, 2005:69-82.

[12]Dixon J, McKee S. Weakly singular discrete Gronwall inequalities[J].Z Angew Math Mech, 1986, 66(11):535-544.

[13]王翠菁，刘文斌，张金陵.非线性分数阶微分方程边值问题解的唯一性[J].河南科技大学学报：自然科学版，2013，34(1)：85-88.

A High Order Scheme for the Numerical Solution of the System of Nonlinear Volterra Integral Equations

WANG Zi-qiang, CAO Jun-ying

(CollegeofScience,GuizhouMinzuUniversity,Guiyang550025,China)

A general technique was presented to construct high order scheme for the numerical solution of the system of nonlinear Volterra integral equations. A so-called block-by-block approach was constructed based on the classical block-by-block method.The unknown solutions at each block step, with exception in the first two, was decoupling in the approach and preserved the good convergence property of the block-by-block schemes. The convergence of the scheme was rigorously established. The numerical solution was proved to converge at the exact solution with order 4.

system of nonlinear Volterra integral equations; high order scheme; convergence analysis

2014-09-24

国家自然科学基金资助项目，编号2012CB025904，11426074；贵州省科学技术项目，编号[2014]2098，[2013]2144；贵州省教育厅项目，编号[2013]405.

王自强(1981-)，男，河南禹州人，副教授，主要从事科学计算和复合材料的多尺度分析研究，E-mail: wangzq@lsec.cc.ac.cn；通讯作者：曹俊英(1981-)，女，河南鹿邑人，教授, 主要从事微分方程数值解研究,E-mail:caojunying1000@126.com.

O241.82

A

1671-6841(2015)01-0001-05

10.3969/j.issn.1671-6841.2015.01.001

期刊基本参数：CN41-1338/N*1962*q*A4*128*zh*P*￥10.00*1 100*26*2015-03