邢灵博，陈 杰，* ，陈志祥

(1.琼州学院理工学院，三亚572022;2.中山大学管理学院，广州510275)

传统高阶马氏链的不足之处是计算转移概率的过程中比较复杂，涉及到的参数过多. 事实上，若为马氏链{Xn，nT，n ＞1}的n 阶转移概率，状态集Ⅰ含有m个元素，则=涉及到的参数多达(m－1)mn个. Raftery 等［1－3］为了简化计算过程，提出了一个新的高阶马氏模型其中Q=(qji)m×m为非负定矩阵且满足列向量元素之和等于1. Ching 等［4］在此理论基础上，提出了具有更一般化的多元马尔可夫链. 多元马尔可夫链是最近兴起的研究领域，是预测方法的重要理论工具之一，其理论成果已广泛应用到库存优化控制［5］、天气预报［6］、风险管理［7］和基因工程［8］等诸多领域.然而，近年来国内外学者对多元马氏链的研究成果主要体现在应用方面，涉及到理论方面的研究很少. 为此，本文在多元马氏理论框架下，对其状态进行分类，并给出相应的基本性质.

1 多元马氏链的基本概念

1.1 多元马氏模型

引理1 (i)设P(mn)表示第n 序列的需求状态到第m 序列状态的转移概率矩阵，且P(mn)为不可约的;为多元马氏链中各种序列于第k 阶段的状态的概率分布，其中(n=1，…，N)表示第n 序列于第k 阶段的状态的概率分布，则存在其中使得Xk+1=AXk，这里A=λmn为 概 率 分布与的关系权数，n，m=1，2，…，N.引理1的证明过程和参数矩阵A 的求解详见文献［9］.

定义1 在满足引理1 的条件下，称Xk+1=AXk为多元马尔可夫模型.

由Xk+1=AXk，可得第n 序列于第k +1 阶段状态的概率分布为由此可见，概率分布与的关系权数为λnm，进而度量了它们之间的关系.因此，该模型不但给出各序列的状态在下阶段的概率分布，同时还进一步表明了其状态概率分布间的关系. 这是多元马氏模型最显著的理论性质之一，利用该性质可以确定不同序列之间的关系，如确定产品需求、DNA 序列等状态之间的关系.

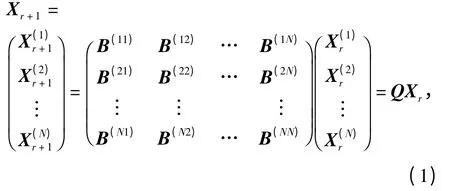
其中

L，K 分别表示状态集所包含元素的个数和库系统的阶数，e 为单位矩阵;而当n≠m 时，

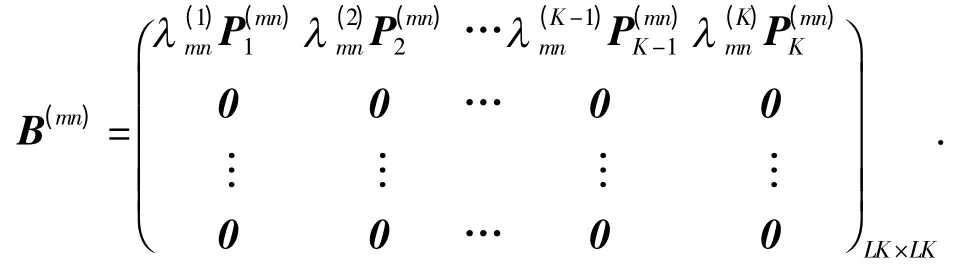
1.2 状态的分类

显然，当n=m 时，指的是单链状态间的可达性和连通性;当n≠m 时，指的是各链状态间的可达性和连通性.这种状态间的关系，是客观存在的普遍现象.比如，不同产品间的需求状态，由于顾客需求的多样性和转移性，从而导致其状态有可能在本状态集内转移，也有可能转移到其他产品的需求状态.

由定义4 可知，当in=im且n =m 时，Tinin为系统从第n 序列的状态in出发，首次返回状态in的时间，这时finin表示系统迟早会返回in的概率.今定义即系统平均首次返回的时间.在竞争市场经济中，可以通过μinin的值确定顾客的首次回头时间，进而分析顾客需求转移的规律性.

由上述的基本定义，多元马氏链的状态可根据以下的定义进行分类:

定义5 若finin=1，则称状态in为常返的;若finin＜1，则称状态in为非常返的;状态in为常返的，若μinin＜+∞，则称其为正常返的;若μinin= +∞，则称其为零正常返的.

定义6 状态in称以t 作为周期的，如果θ 不是t 的整倍数时，有;同时存在k0，使得对于任意k ＞k0，有＞0.若t=1 且状态in为正常返的，则称之为遍历状态.

2 主要结果

2.1 多元马氏模型的切普曼－柯尔莫哥洛夫方程

为了进一步深入了解多元马氏模型状态间关系的基本性质，以便分析各状态间的转移规律，首先给出多元马氏模型的切普曼－柯尔莫哥洛夫方程.

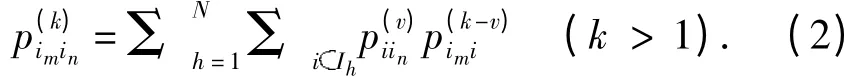
证明 由题设可知，系统是由N 条单元马氏链构成的，各链的状态集含有的元素个数为L. 因此，该系统由第n 序列的状态in出发历经v个阶段后到达的序列有N 种可能，而可能到达的状态有N ×L种.再由的定义可知为该系统从第n 序列状态in出发历经k个阶段后到达第m 序列状态im的转移概率.因此，利用全概率公式和马氏性，可得:

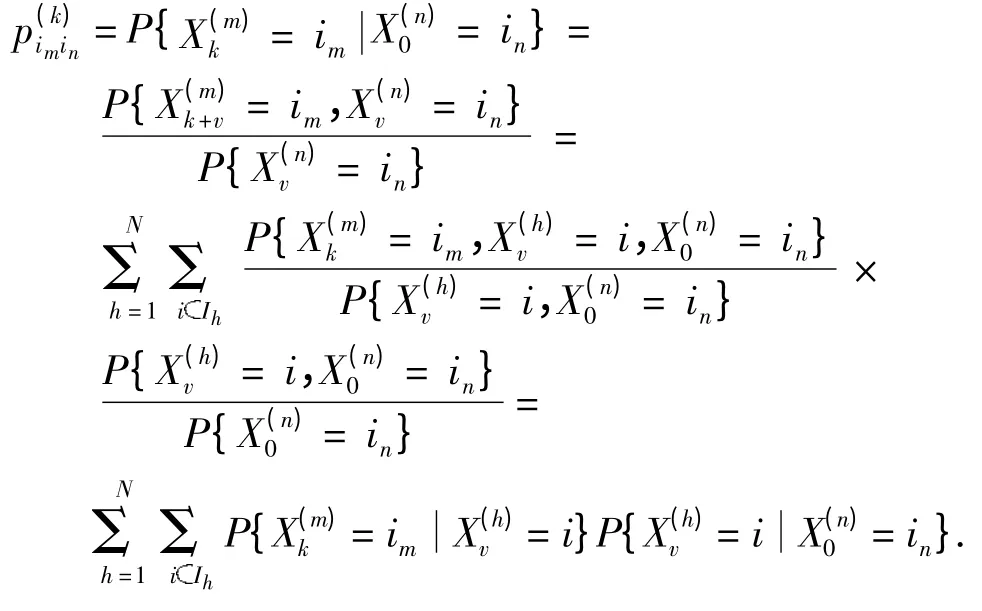
今称式(2)为多元马氏模型的切普曼－柯尔莫哥洛夫方程.该方程在计算高阶转移概率的过程中起着非常重要的作用，通过该公式可以化高阶的转移概率为低阶的来计算.

2.2 状态间关系的基本性质

有了多元马氏模型的切普曼－柯尔莫哥洛夫方程，接下来主要研究各链状态间关系的基本性质.

定理2 设in为多元马氏模型第n 序列的状态(n=1，2，…，N)，如果in1→in2，in2→in3，则in1→in3.

证明 因为in1→in2和in2→in3，所以存在k1和k2，分别使得和因此，根据多元马氏模型的切普曼－柯尔莫哥洛夫方程，可得:证毕.

定理3 多元马氏模型各序列间互通的状态，具有下列性质:①满足对称性，即若in↔im，则im↔in.②满足传递性，即若in1↔in2及in2↔in3，则in1↔in3.

证明 ①因为in↔im，所以存在k1和k2，分别使得和，故有im↔in.②由题设可知存在k1，k2，k3和k4，分别使得和，再由多元马氏模型的切普曼－柯尔莫哥洛夫方程，有:

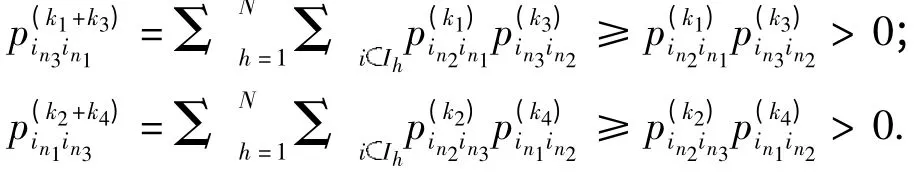
因此，有in1↔in3.证毕.

定理4 设in，im分别为多元马氏模型第n 序列和第m 序列的状态(n，m=1，2，…，N)，如果in↔im，则状态in，im满足以下的性质:(i)同为常返的或同为非常返的;(ii)in和im具有相同的周期.

证明 (i)因为in↔im，所以存在k1≥1 和k2≥1，分别使得和由多元马氏模型的切普曼－柯尔莫哥洛夫方程，可得:

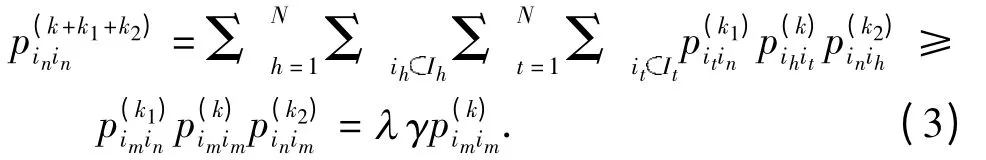
同理，可得:

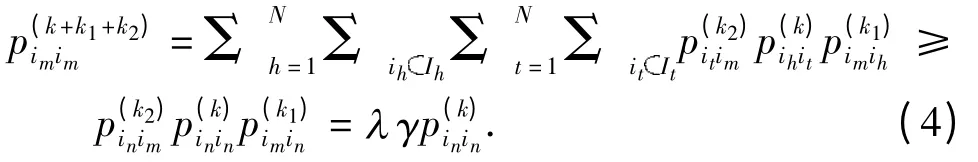
由级数敛散性的比较准则［11］并结合式(3)和式(4)，可知和同时收敛或发散.因此，只需证的敛散性是in或im为常返性(常返的或非常返的)的充分条件，即可得命题的结论. 若为发散级数，则有由两边求和，可得:

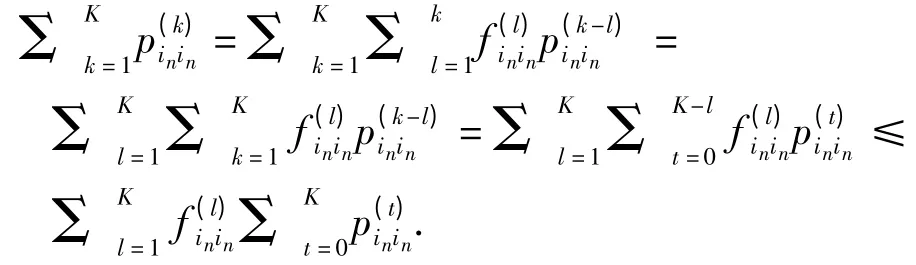
于是，对上式进行分离整理，可得:

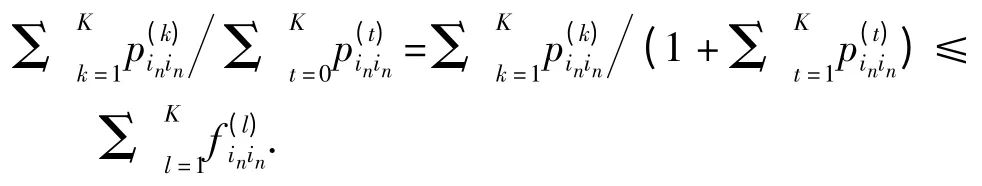
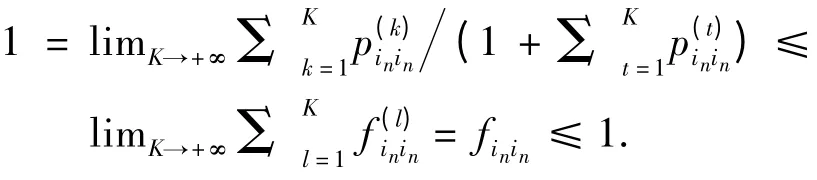
再由极限的迫敛准则，可知finin=1，故in为常返的.若为收敛级数，则因此，当k→+∞时，故in为非常返的. 根据和同敛散性，即可得出im相应的常返性.

(ii)设tn，tm分别为状态in和状态im的周期，故存在和，对于任意k≥及k≥，有及又因为in↔im，所以存在kn及km，分别使得和再由多元马氏模型的切普曼－柯尔莫哥洛夫方程，可得:

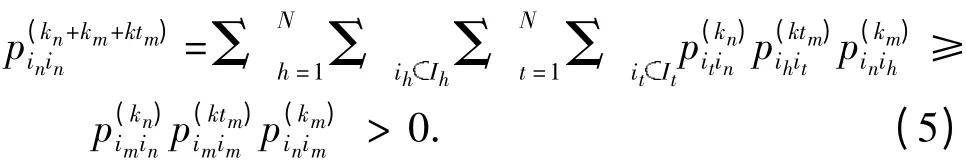
因此，kn+km+ktm为tn的整倍数.同理，可证得kn+km+(k+1)tm为tn的整倍数. 于是，存在k1和k2，分别使得kn+km+ktm=k1tn及kn+km+(k+1)tm=k2tn，故tm=(k2－k1)tn.利用式(5)，同理可证:存在ˉk1和ˉk2，分别使得kn+km+ktn=及kn+km+(k+1)tn=，得tn=()tm.因此，k2－k1=－=1，故tn=tm.证毕.

［1］Raftery A E. A model for high-order Markov chains［J］.Journal of the Royal Statistical Society:Series B，1985，47(3):528－539.

［2］Raftery A，Tavare S. Estimation and modelling repeated patterns in high order Markov chains with the mixture transition distribution model［J］. Applied Statistics，1994，43(1):179－199.

［3］Berchtold A，Raftery A E. The mixture transition distribution model for high-order Markov chains and non-Gaussian time series［J］. Statistical Science，2002，17(3):328－356.

［4］Ching W K，Fung E S，Ng M K. A multivariate Markov chain model for categorical data sequences and its applications in demand predictions［J］. IMA Journal of Management Mathematics，2002，13(3):187－199.

［5］Ching W K，Fung E S，Ng M K. A higher-order Markov model for the Newsboy's problem［J］. Journal of the Operational Research Society，2003，54(3):291－298.

［6］Yang H，Li Y，Lu L，et al. First order multivariate Markov chain model for generating annual weather data for Hong Kong［J］. Energy and Buildings，2011，43(9):2371－2377.

［7］Siu T K，Ching W K，Fung S E，et al. On a multivariate Markov chain model for credit risk measurement［J］.Quantitative Finance，2005，5(6):543－556.

［8］Ching W K，Fung E S，Ng M K. Higher-order Markov chain models for categorical data sequences［J］. Naval Research Logistics (NRL)，2004，51(4):557－574.

［9］Ching W K，Ng M K. Markov chains:Models，algorithms and applications［M］. New York:Springer，2006.

［10］Ching W K，Ng M K，Fung E S. Higher-order multivariate Markov chains and their applications［J］. Linear Algebra and Its Applications，2008，428(2):492－507.

［11］华东师范大学数学系. 数学分析［M］. 2 版. 北京:高等教育出版社，1991.