金小微，张启敏

(宁夏大学数学与计算机学院，银川750021)

考虑如下具有年龄结构带Poisson 跳的随机种群扩散方程［1］

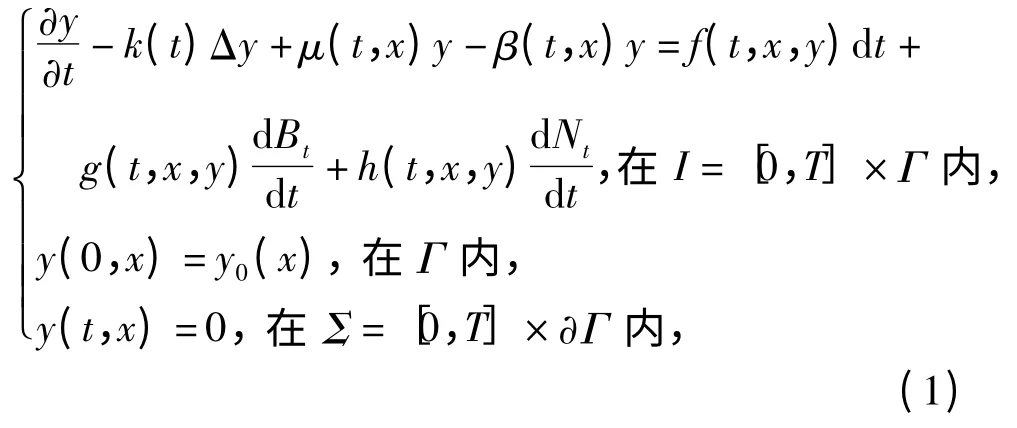
种群系统引起了许多学者的关注［2-6］. 例如，李健全和陈任昭［2］介绍了具空间扩散和年龄结构的种群系统的最优分布控制，Zhang［3］证明了具有年龄结构的随机种群扩散模型数值解的指数稳定性. Wang 等［4］运用半隐式欧拉法讨论了具有年龄结构带Poisson 跳的随机种群方程的收敛性.

上述文献中不确定因素为随机环境的影响. 然而，现实生活中，我们研究的系统不仅受到随机环境的影响，还会受到模糊不确定性的影响. 例如，出生率、死亡率等. 因此，把模糊理论引入到种群模型(1)中更符合实际意义. 考虑如下带Poisson 跳的模糊随机种群扩散方程

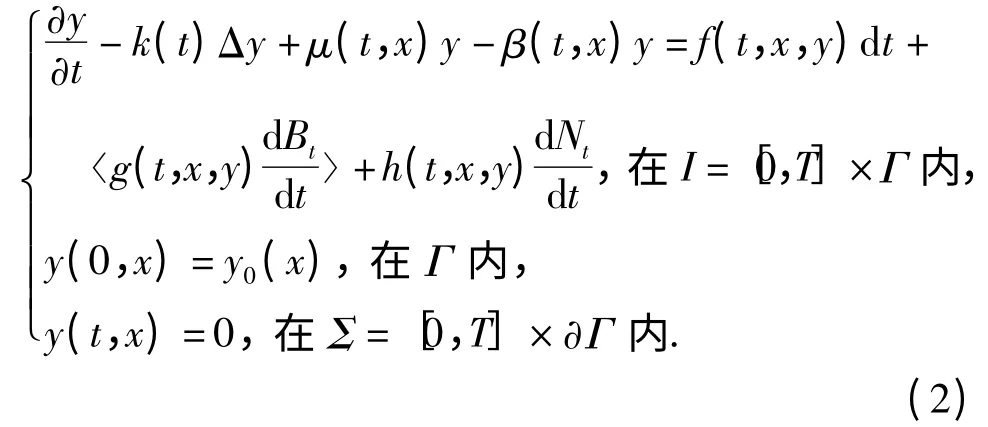
利用文献［7］-［9］中模糊Itô 积分的定义，讨论带Poisson 跳的模糊随机种群扩散方程强解的存在性和唯一性.本文所讨论模型和得到的结论是文献［1］的扩展.

1 预备知识

根据Zadeh 的扩张原理定义模糊数的函数，线性运算的α 水平集满足区间运算式

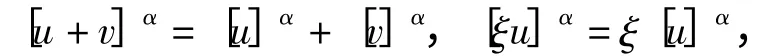
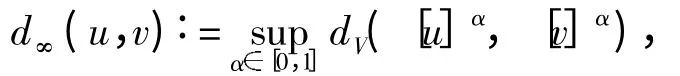
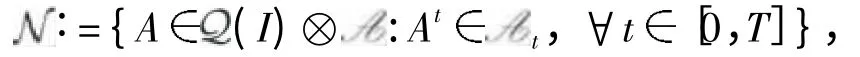
这里At={ω:(t，x，ω)A}.

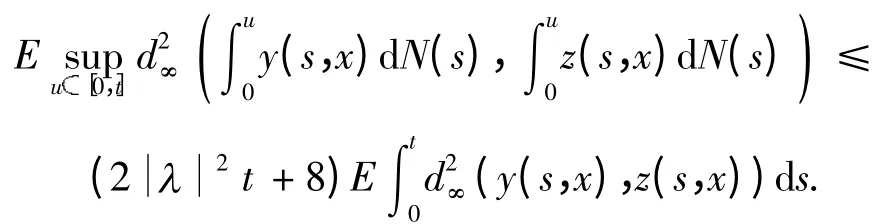
证明过程与文献［7］类似.

2 解的存在唯一性

考虑带Poisson 跳的模糊随机种群扩散方程

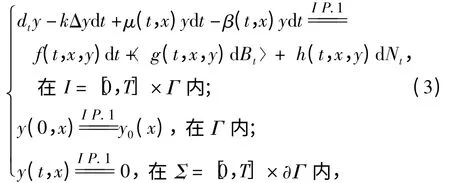
且y0:Ω→(V)是一个模糊随机变量.

定义2 模糊随机过程yt:Ⅰ×Ω →(V)被称为方程(3)的强解，如果满足

(1)yt2(Ⅰ×Ω，;(V));

(2)yt是一个d∞-连续的模糊随机过程;

(3)满足

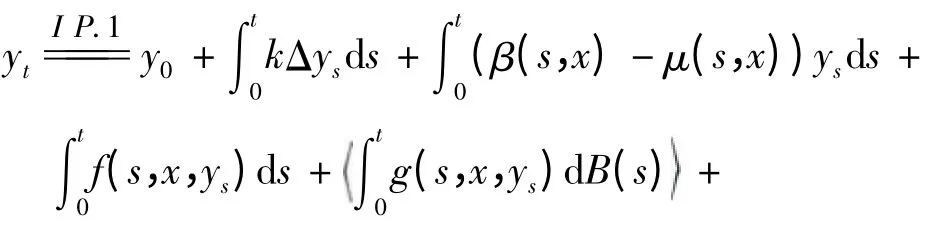
这里yt=y(t，x)，y(t，x)=0，Σ=［0，T］×∂Γ.

定义3 方程(3)的强解y1t:Ⅰ×Ω →(V)是唯一的，如果

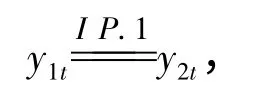
其中y1t=y1(t，x)，y2t=y2(t，x)且y2t:Ⅰ×Ω→(V)是方程(3)的任意强解.

为了证明本文的主要结论，给出以下假设条件:

(c0)μ(t，x)、β(t，x)和k(t)均是非负可测的，

(c1)存在一个常数L ＞0，对∀u，v(V)使得

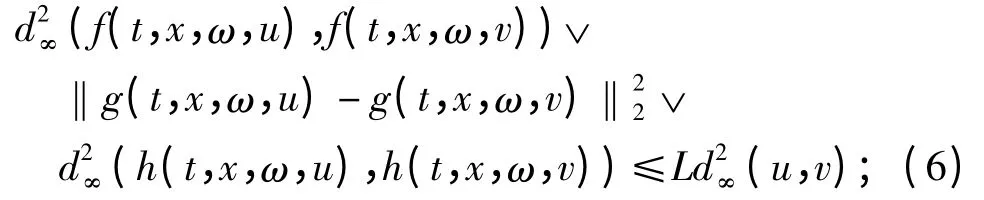
(c2)存在一个常数C ＞0，对∀u(V)，∀(t，x)Ⅰ使得

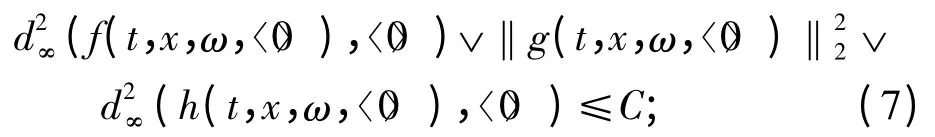
(c3)存在一个常数M ＞0，对∀u，v(V)，使得

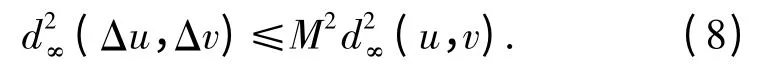
下面运用逐次逼近法证明方程(3)解的存在性.首先，定义一个Picard 序列:Ⅰ×Ω →(V)，当n=0 时

当n=1，2，…时

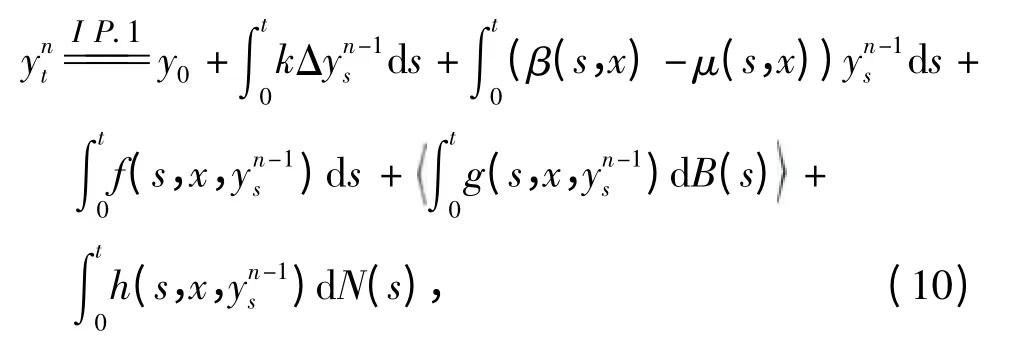
引理1 假设y0是一个0 -可测的随机变量，满足(y0，<0> )＜∞，若f:Ⅰ× Ω ×(V)→(V)，g:Ⅰ×Ω ×(V)→L(K，V)，h:Ⅰ×Ω ×(V)→(V)，且条件(c0)～(c3)成立. 则满足下列不等式

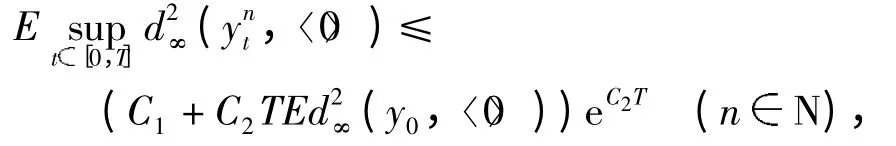
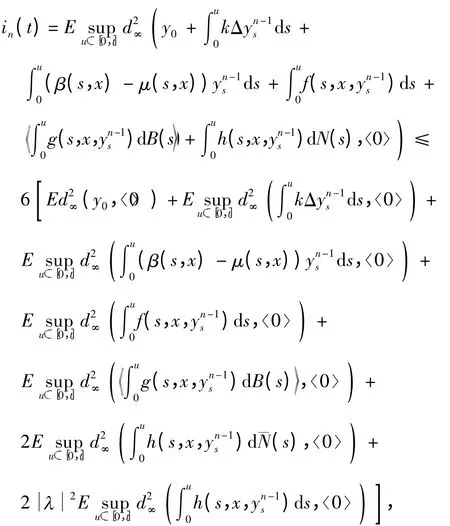
根据条件(c0)～(c3)和文献［7］以及三角不等式，可得

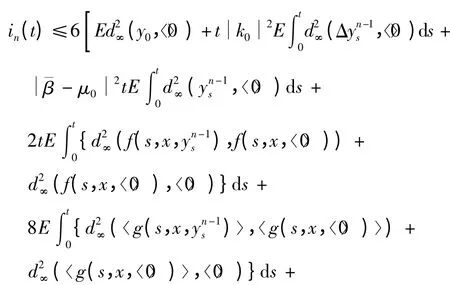
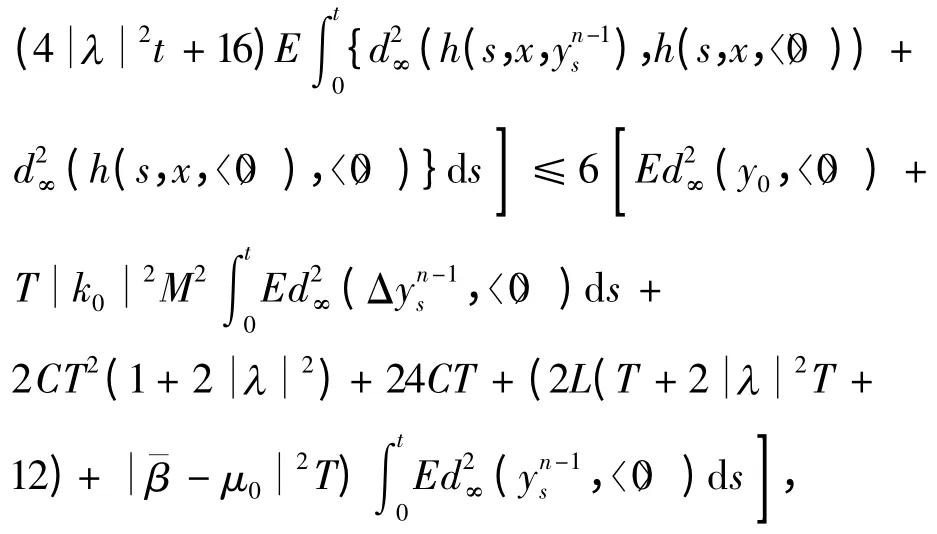
由最后一个不等式有

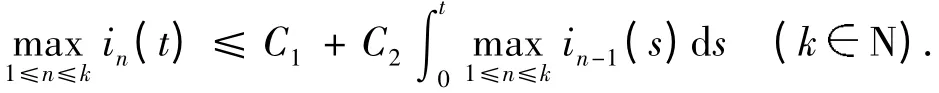
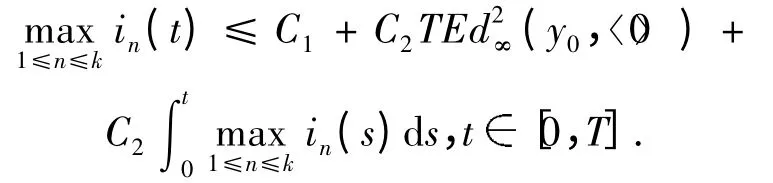
再由Gronwall 引理得证

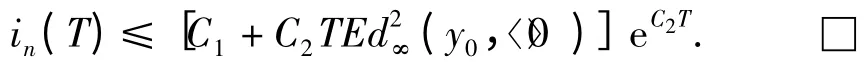
定理1 令y02(Ⅰ×Ω，0，P;(V)). 假设f:Ⅰ×Ω×(V)→(V)，g:Ⅰ×Ω×(V)→L(K，V)，h:Ⅰ×Ω×(V)→(V)满足条件(c0)～(c3)，则方程(3)存在唯一的强解yt.

证明 记

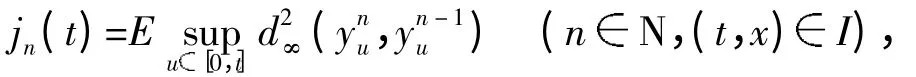
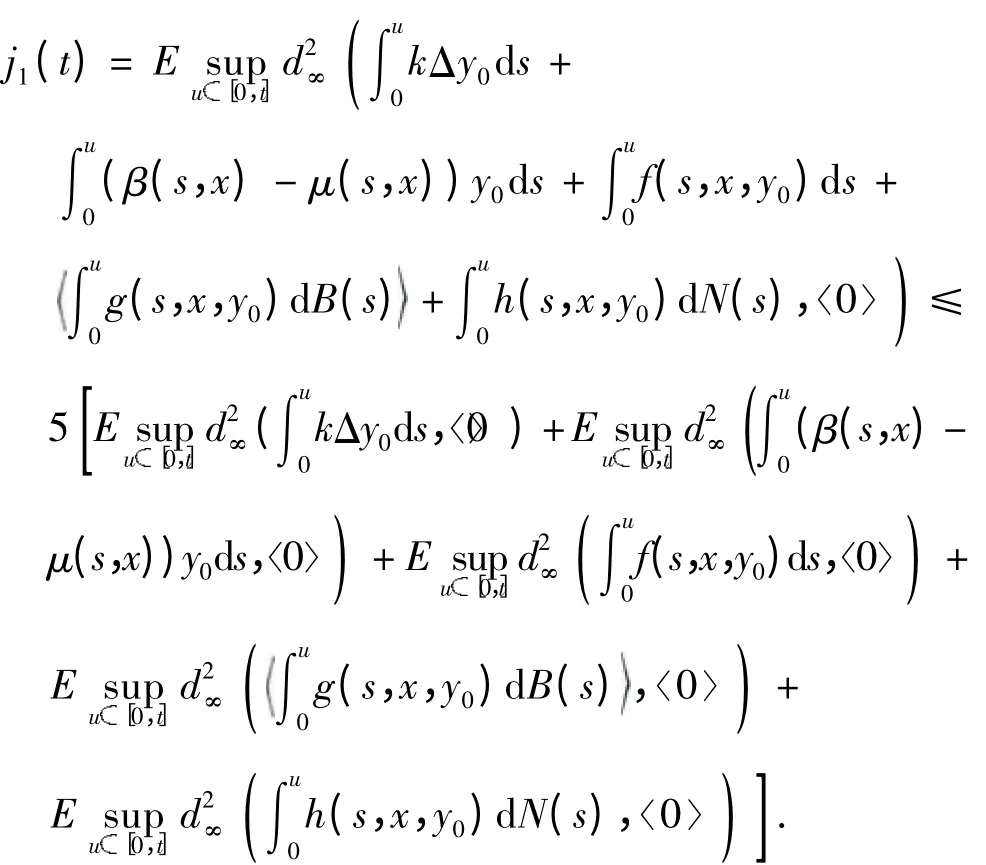
由性质1、文献［7］以及条件(c1)、(c2)可得

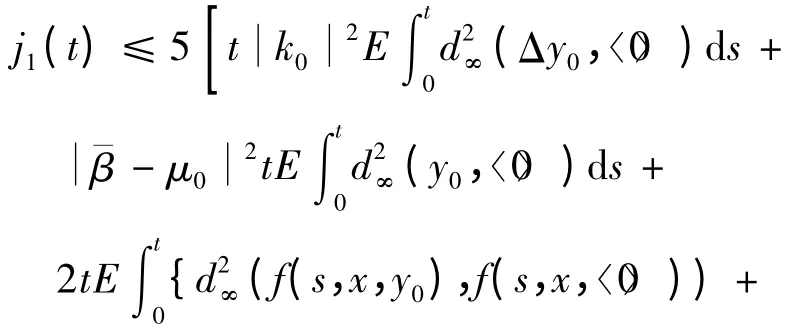
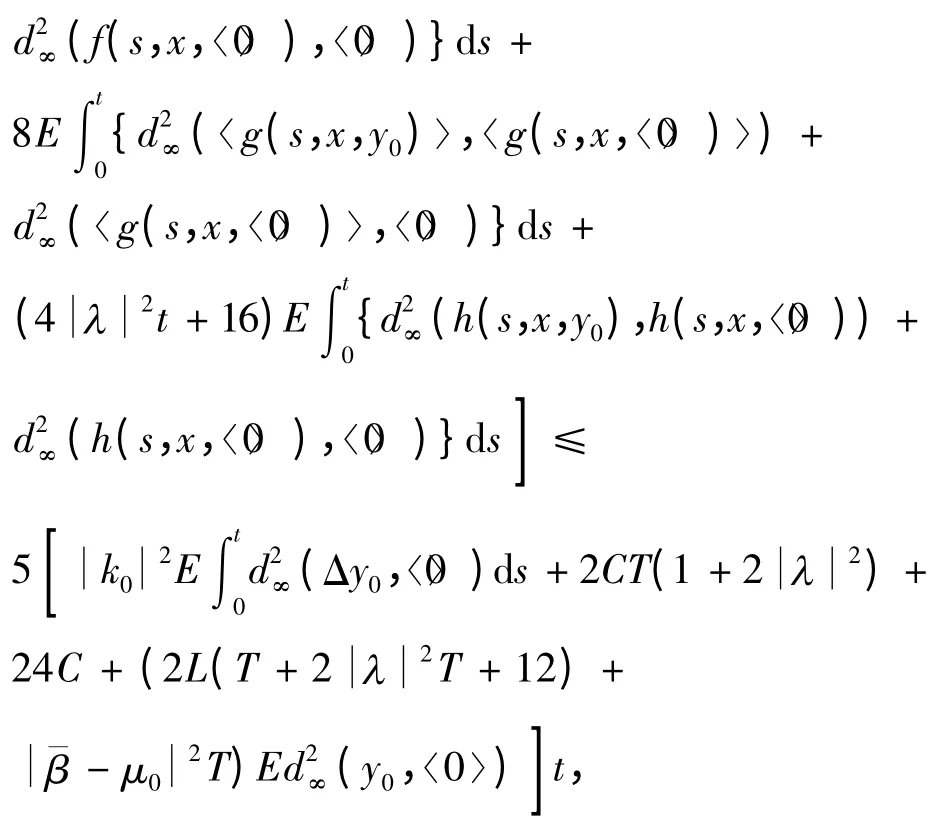
因此，j1(t)≤K1t，∀(t，x)Ⅰ，其中

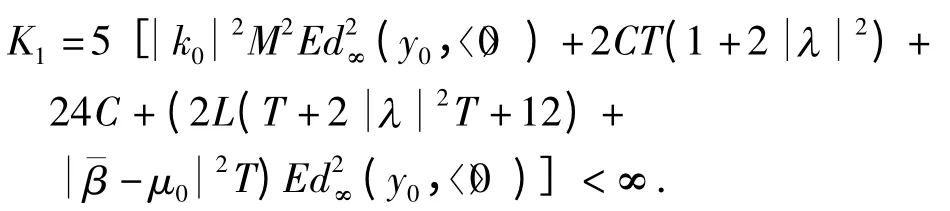
类似地，运用条件(c0)、(c1)和(c3)，可得

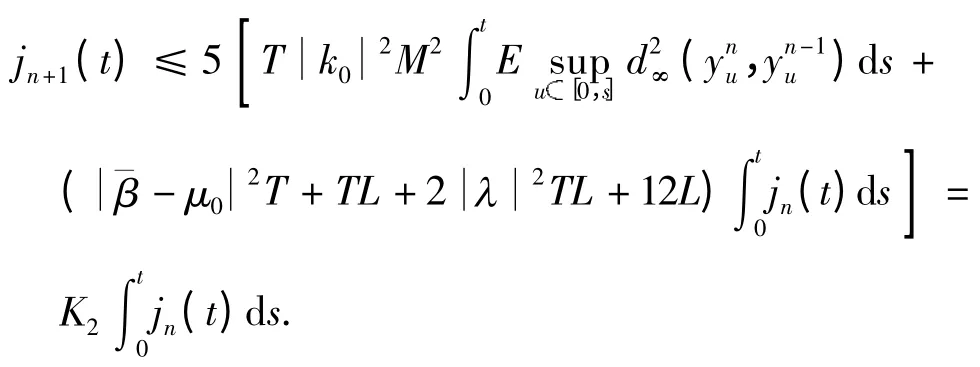
因此可以推断

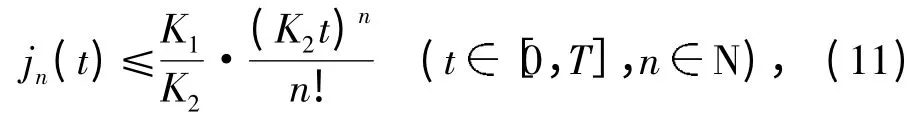
由Chebyshev 不等式和式(11)可得

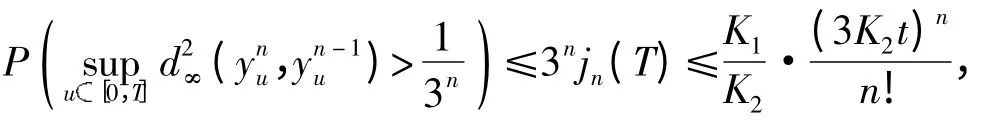
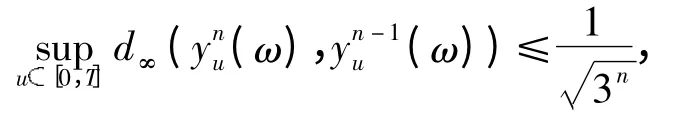
其中n≥n0，那么在概率1 的意义下，{yn(·，ω)}在(t，x)Ⅰ上一致收敛到d∞-连续函数yt≡y(·，Ω):Ⅰ→(V)，∀ωΩc，则yt是一个连续的-适应模糊随机过程. 由于Ω;(V))，我们有，对任意固定的t［0，T］和xΓ，模糊随机变量(t，x)(Ω，，P;(V)).即对∀t［0，T］，xΓ，(y(t，x)，<0> )x)，<0> )＜∞，即yt2(Ⅰ×Ω;(V)).

下面将证明yt是式(3)的一个解. 对每个t［0，T］，xΓ，有

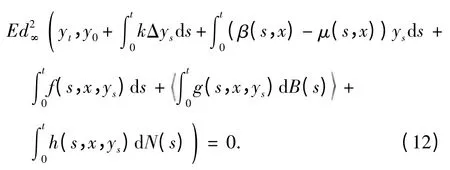
事实上，我们可以得到

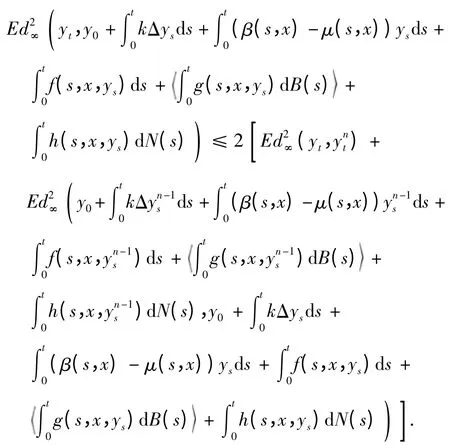
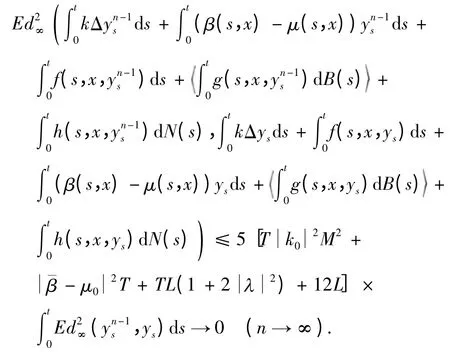
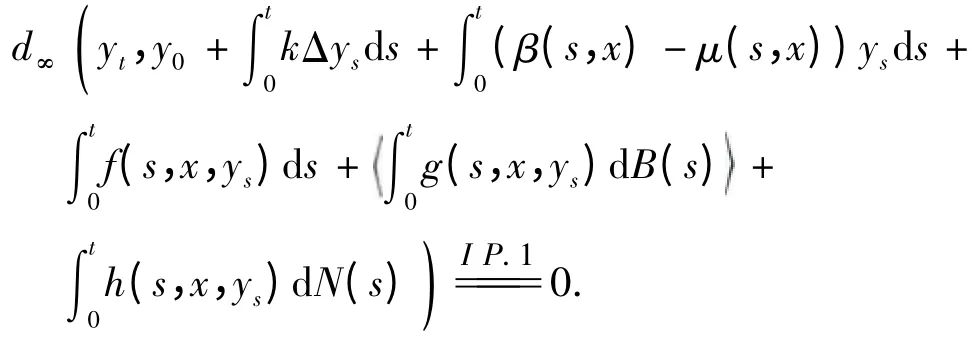
因此yt满足方程(3).

下面证明yt是唯一强解. 假设yt，zt:Ⅰ× Ω→(V)均是方程(3)的解.对于每个t［0，T］，定义(y(u)，z(u)).由此可得

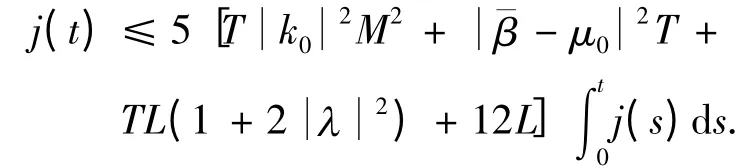
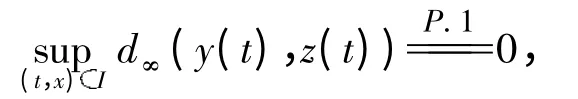
定理得证.□

以上证明用到Picard 迭代来逼近方程(3)的解，下面的定理给出了Picard 迭代的估计.

定理2 假设y0:Ω →(V)，f:Ⅰ×Ω×(V)→(V)，g:Ⅰ×Ω×(V)→L(K，V)，h:Ⅰ×Ω×(V)→(V)满足条件(c0)～(c3)，yt是方程(3)的唯一解是式(10)定义的Picard 迭代，则

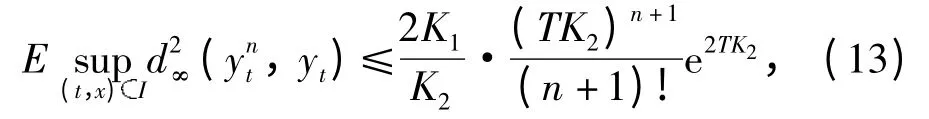
其中K1和K2为定理1 中定义的常数.

证明 记

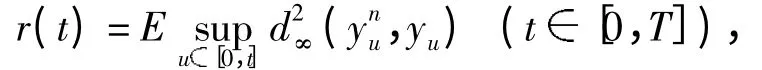
由性质1、文献［7］及条件(c0)、(c1)、(c3)，有

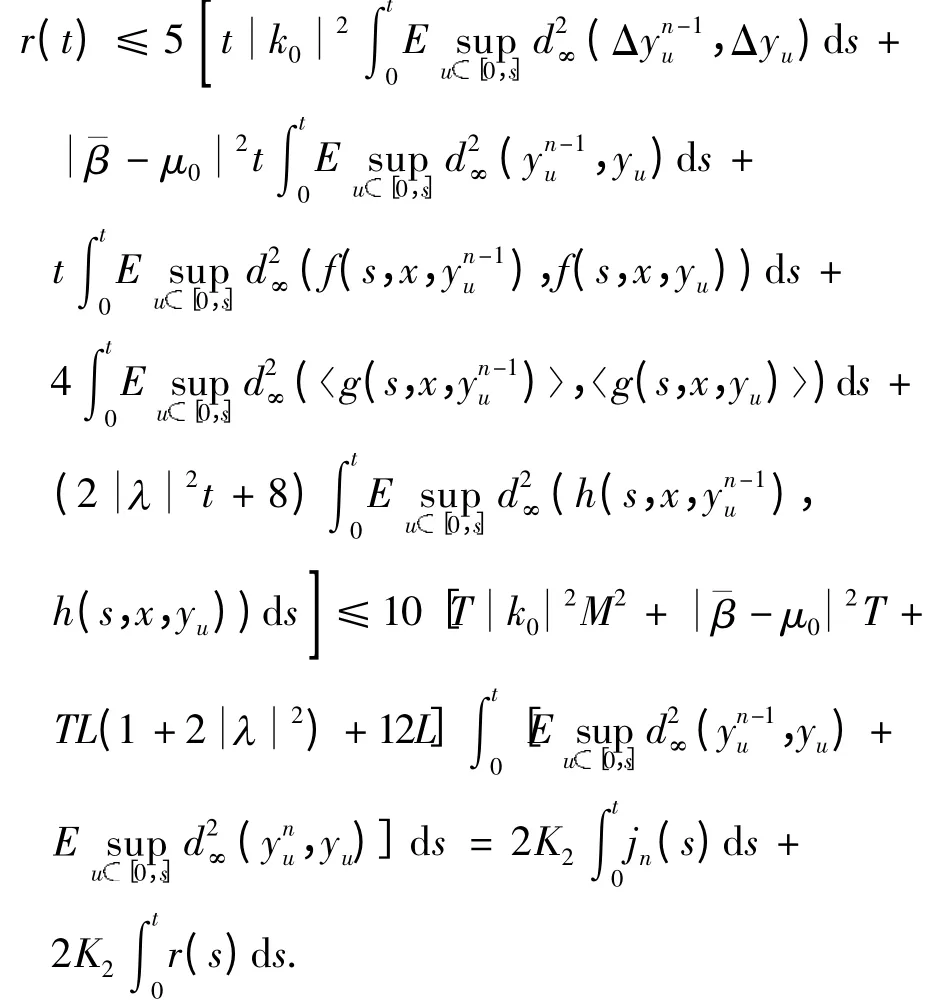
运用式(11)有

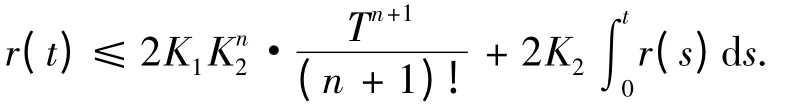
由Gronwall 不等式得式(13)成立.由定理2 得

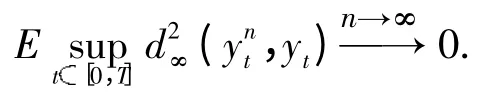
于是可得具有年龄结构带Poisson 跳的模糊随机种群扩散方程的近似解

［1］Li R H，Pang W K，Wang Q H. Numerical analysis for stochastic age-dependent population equations with Poisson jumps［J］. Journal of Mathematical Analysis and Applications，2007，327:1214 -1224.

［2］李健全，陈任昭. 具空间扩散和年龄结构的种群系统的最优分布控制［J］. 华南师范大学学报:自然科学版，2004(4):29 -36.Li J Q，Chen R Z. Optimal distributed control of population dynamic with spatial-diffusion and age-structure［J］.Journal of South China Normal University:Natural Science Edition，2004(4):29 -36.

［3］Zhang Q M. Exponential stability of numerical solutions to a stochastic age-dependent population system with diffusion［J］. Journal of Computational and Applied Mathematics，2008，220:22 -33.

［4］Wang L S，Wang X J. Convergence of the semi-implicit Euler method for stochastic age-dependent population equations with Poisson jumps［J］. Applied Mathematical Modelling，2010，34:2034 -2043.

［5］李建全.年龄相关的非线性种群扩散系统最优分布控制的必要条件［J］. 华南师范大学学报:自然科学版，2007(1):1 -7.Li J Q. Necessary conditions of optmal distributted control for age-dependent nonlinear population diffusion system［J］. Journal of South China Normal University:Natural Science Edition，2007(1):1 -7.

［6］李建全，陈任昭. 一类非线性种群扩散系统最优分布控制的存在性［J］. 华南师范大学学报:自然科学版，2005(4):4 -9.Li J Q，Chen R Z. Existence of the optmal distributed control for a class of nonlinear population diffusion system［J］. Journal of South China Normal University:Natural Science Edition，2005(4):4 -9.

［7］Malinowski M T. Strong solutions to stochastic fuzzy differential equations of Itô type［J］. Mathematical and Computer Modelling，2012，55:918 -928.

［8］Malinowski M T. Itô type stochastic fuzzy differential equations with delay［J］. Systems ＆ Control Letters，2012，61:692 -701.

［9］Malinowski M T，Michta M. Stochastic fuzzy differential equations with an application［J］. Kybernetika，2011，47:123 -143.