孙丽雪， 李永彬， 林 晨

(电子科技大学数学科学学院，四川成都611731)

1 引 言

高等代数中介绍了线性子空间的交与和，对于线性子空间的并，多数教材中并未详细讨论.本文主要讨论了特征为零的域上的有限维线性空间中有限个非平凡子空间的并这个问题，并试图用更本质的方法证明：特征为零的域上的有限维线性空间中互不包含的非平凡子空间的并不能构成线性子空间.

文献[1]中给出了一个相当巧妙的证明，本文一方面结合商空间的维数公式给出一个改进证法，另一方面结合代数几何中仿射代数簇的一个简单性质给出了另一个更为简洁的证法.

首先，对于线性空间的子空间，在各版教材(文献[1],[2],[3])习题中有下述结论，设Fn是数域F上的全体n维向量构成的线性空间，则Fn的任一子空间V1必至少是一个n元齐次线性方程组的解子空间.而商空间是我们不太熟悉的一个概念，在文献[2]中详细介绍了这个概念及商空间的维数公式.

从上述线性空间中任一子空间与齐次线性方程组解子空间的关系，及商空间的维数公式，文中讨论了特征为零的域上的有限维空间上有限个子空间的并集是否是子空间这一问题，并且给出否定回答，从而这个并集不是原来的线性空间.

其次，由线性子空间与仿射簇概念的相似性，引出仿射簇的定义.从而考虑仿射簇的并，不同的是仿射簇虽与子空间定义类似，但仿射簇的定义方程不要求是线性的，从而仿射簇的并与子空间的并的性质也不相同，由此可以更好地理解子空间与仿射簇的区别.

最后，由每个线性子空间可以找到一个包含它的仿射簇，从仿射簇的角度，同样得出，该并集不是原来的线性空间.

2 特征为零的域上的有限维线性空间V上子空间的并集

在线性空间这一章中，有下述结论：

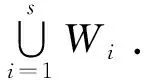
为证明上述定理，通常证明V中至少有一个向量不属于W1,W2,…,Ws中任何一个，并用数学归纳法来证.即先证明s=2时定理成立，然后设s=k时成立，证明s=k+1时定理也成立即可，详见[2].

下面首先介绍域的特征的概念.

定义1设F为域，如果存在最小的正整数n，使得对所有的a∈F，有na=0，则称n为域F的特征.如果这样的正整数不存在，则称域F的特征为零.

注意，特征为零的域一定是无限域.因为有限域可以看作关于加法运算构成了一个群，所以这个群的阶数就是有限的，从而一定存在最小的正整数n，使得对于域中所有的元素a，都有na=0.

再来介绍商空间的一些知识.

对于α1,α2∈V,c∈F，在V/W中定义加法和数乘如下：

定义2[2]设W是域F上线性空间V的子空间，V/W是V对模W的同余类全体，则V/W是域F上的线性空间，称为商空间.

引理1[2]商空间的维数公式：dimV/W=dimV-dimW

以下在[1]中证法的基础上，借助引理1，我们给出定理1的一个替代的证明.

证法一用反证法.假设W=W1∪W2∪…∪Ws构成子空间，且不妨设W⊂Fn.由于任一线性空间的子空间都是一个齐次线性方程组的解子空间，对每个i(i=1,2,…,s)，不妨设Wi均为n-1维子空间(不然将Wi扩大即可)，设以Wi为解子空间的线性方程分别为

ai1x1+ai2x2+…+ainxn=0，i=1,2,…,s.

由这些方程导出关于未定元T的多项式

fi(T)=ai1+ai2T+ai3T2+…+ainTn-1，i=1,2,…,s.

对每一个i，fi(T)最多有n-1个根，故这些多项式最多有s(n-1)个根.而F中有无限多个元素，因此存在t∈F，使得fi(t)≠0，即

ai1+ai2t+ai3t2+…+aintn-1≠0，i=1,2,…,s.

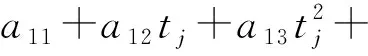
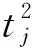
注 该以上证法与[1]中给出的证法没有太大的差异，但能较好的理解定理1的结论.下节给出一种更为简洁和本质的证法.

3 另一种证法

由线性子空间与仿射簇二者概念的相似性，引入下面仿射簇的概念，详见文献[5].

定义3[5]设F是一个域，f1,f2,…,fs是Fx1,x2,…,xn中的多项式.令集合

V(f1,f2,…,fs)=(a1,a2,…,an)∈Fn对所有的1≤i≤s都有fi(a1,a2,…,an)=0，

则称V(f1,f2,…,fs)是由f1,f2,…,fs定义的仿射簇.

由定义可知，V(f1,f2,…,fs)是使得所有f1,f2,…,fs等于零的点的集合.线性空间的任一子空间对应一个n元齐次线性方程组的解子空间，而在仿射簇的定义中没有要求它的定义方程是线性的，因而子空间可以看作是特殊的仿射簇，仿射簇是子空间的推广.那么对应子空间的并，仿射簇的并还是仿射簇吗？下面定理2讲述了这个问题.

定理2如果V,W⊂Fn是仿射簇，证明V∪W也是仿射簇.

证假设V=V(f1,f2,…,fk)，W=V(g1,g2,…,gl)，其中k和l为正整数.则有V∪W=V(fpgq:1≤p≤k,1≤q≤l).一方面，如果(a1,a2,…,an)∈V，那么所有的fp在这一点为0，也就蕴含着所有的fpgq在(a1,a2,…,an)点也等于0.因此V⊂V(fpgq).类似地，有W⊂V(fpgq).这就证明了V∪W⊂V(fpgq).

另一方面，取(a1,a2,…,an)∈V(fpgq)，如果该点在V中，那么就完成了证明.如果该点不在V中，那么对某个p0，有fp0(a1,a2,…,an)≠0.又因为fp0gq对所有的q，在(a1,a2,…,an)点都等于0，那么gq一定在这个点为0，这就证明了(a1,a2,…,an)∈W.于是得到V(fpgq)⊂V∪W.

综上有V∪W=V(fpgq).因此V∪W也是仿射簇.

从定理2的证明过程可见下述推论1显然成立.

推论1设f,g∈Fx1,x2,…,xn，则有V(f)∪V(g)=V(fg).

定理2蕴含着有限个仿射簇的并集还是仿射簇，只需将这有限个仿射簇的定义方程写出来即可证明.

从定理2可以看到子空间的并不同于仿射簇的并，二者既有联系又有区别.

以下从仿射簇的角度证明定理1.

定理1证法二与第一种证法类似，对每个i，不妨设Wi均为n-1维子空间(不然将Wi扩大即可)，设以Wi为解子空间的线性方程分别为

ai1x1+ai2x2+…+ainxn=0，i=1,2,…,s.

对于每个i，ai1x1+ai2x2+…+ainxn=0表示一个超平面.

显然g为s次齐次多项式，现设h=g(1,t,…,tn-1)∈F[t]，则有h(t)在F上最多有有限个根. 而F中有无限多个元素，因此存在tj∈F(j=0,1,2,…,n-1)，使得h(tj)≠0.

[参 考 文 献]

[1] 张贤科,许甫华.高等代数学 [M]. 2版.北京:清华大学出版社，2004.

[2] 丘维声.高等代数学习指导书(上、下册)[M].北京:清华大学出版社，2009.

[3] 黄廷祝,何军华,李永彬.高等代数[M].北京:高等教育出版社，2012.

[4] 韩士安,林磊.近世代数 [M]. 2版.北京:科学出版社，2009.

[5] David Cox,John Little,Donal o’shea.Ideal Varieties,and Algorithms [M]. 2nd. Ed. New York: Springer，2006.