李明奇， 杜鸿飞

(电子科技大学数学科学学院，四川成都610054)

1 引 言

随着计算机仿真技术的发展，很多实验和设计可以通过计算机仿真实现. 利用计算机仿真技术进行实验，可使学生获得感性知识，经历从实践到理论的认知过程. Matlab软件在基础课程的仿真教学实践中，常常可以弥补常规实验方法中实验成本高、实验环境要求高，实验效率较低等诸多缺陷. 如何将传统的纯理论推导与计算机仿真结合起来，提高学生的编程能力和创新思维能力，越来越受到各课程一线教师的重视[1，2].

本文以函数最优解为教学设计内容，探讨如何通过对相同问题进行不同层面的Matlab模拟仿真，展示函数的性质, 促进学生对优化问题求解方法的深入思考. 通过各个不同角度展现函数的图形特征，加深学生对所研究问题求解过程的理解和求解方法的掌握，增强直观性改善教学效果.

2 函数特征分析

函数极值点的分布是许多最优化问题中的关键问题. 因此，函数的图形特征描述是微积分、微分方程、最优化等课程中的重要内容[3-5]. 下面，以二元函数

u(x,y)=x2+y2-cos3πx-cos4πy+x+y+1

(1)

为例，寻找其极值点的分布规律. 根据函数极值点的驻点特征知，函数u(x，y)的两个偏导等于零，于是

(2)

直接求解方程组(2)不容易. 为此，可以用Matlab作其三维曲面图(如图1)，通过图形寻找极值分布规律. 从图1看出，函数u(x，y)具有无穷的极值点，且曲面具有波动性. 如果需要在给定的范围内寻找函数的最大值，那么从图1就可以观察到其最大值点的大概分布位置. 据此，可以通过设计算法，快速收敛到我们需要的最值点，避免由于算法设计的局限性收敛到某个局部的极大值点.

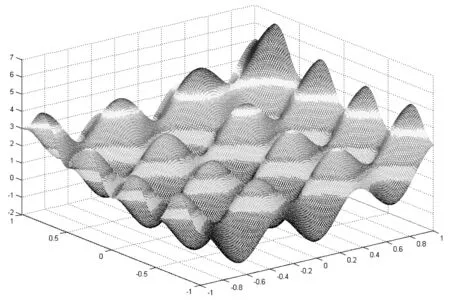
图1 函数u(x,y)的曲面

通过图1可以看出极值点所处的范围. 然而，要通过图1给函数u(x，y)极值点定位还是不行的. 为此，可以换一个角度，从等高线图的分布进行研究. 函数u(x，y)的二维等高线分布和颜色分布显示函数值的分布特征，如图2. 以此，可以对极值点进行更准确的定位.

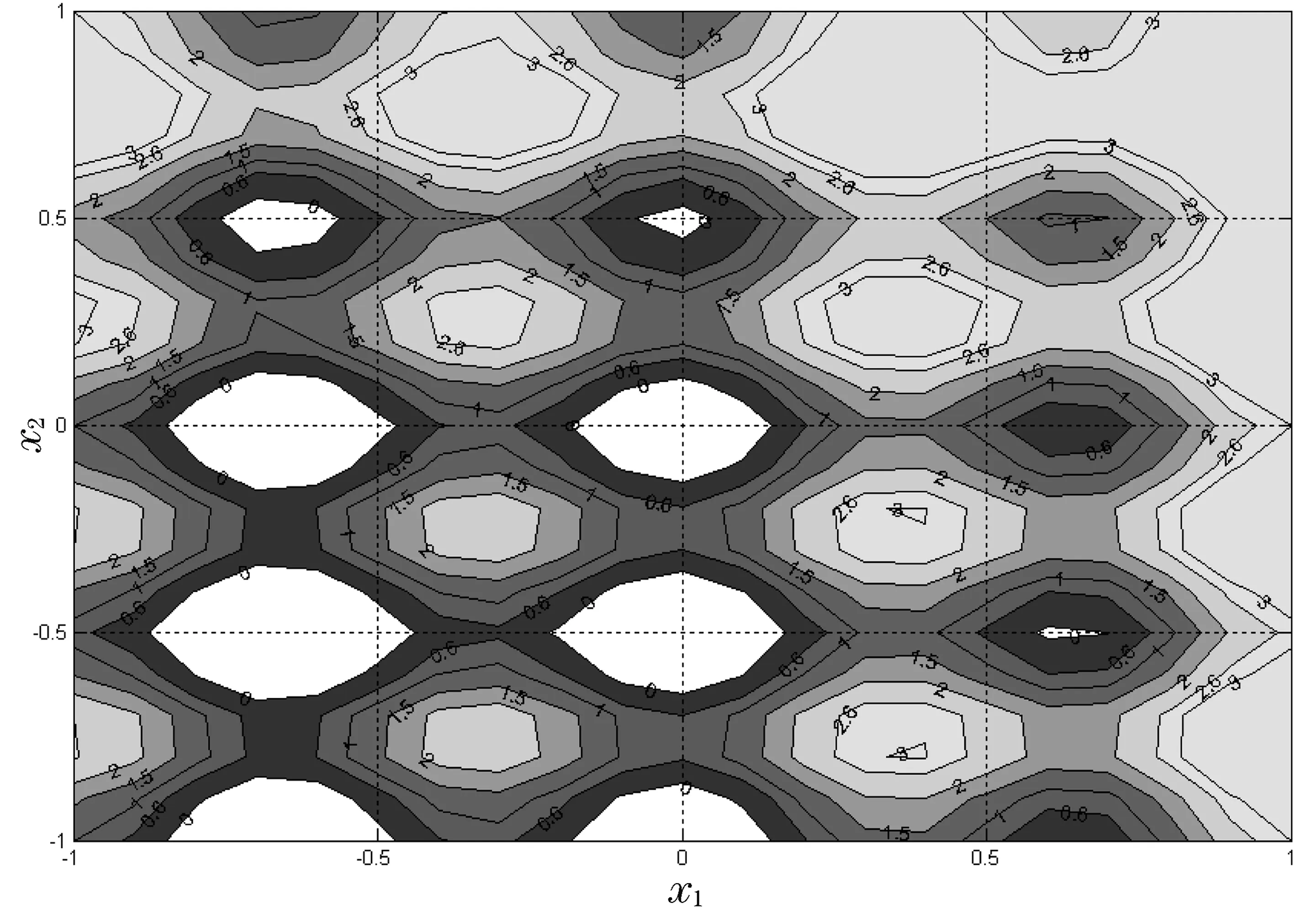
图2 函数u(x,y)的二维等高线图

为了进一步了解函数值的趋势，可以引入羽箭图，箭头方向指示函数值增大的方向，如图3. 图3更清楚地显示的等高线数值和羽箭可以非常直观显示函数值随自变量的变化趋势. 同时，图3显示了极值点的位置信息，为其坐标的估计提供参考. 函数u(x，y)的三维等高曲线图如图4，其中的封闭曲线都是等高线.

图3 函数u(x,y)的二维等高线与梯度图

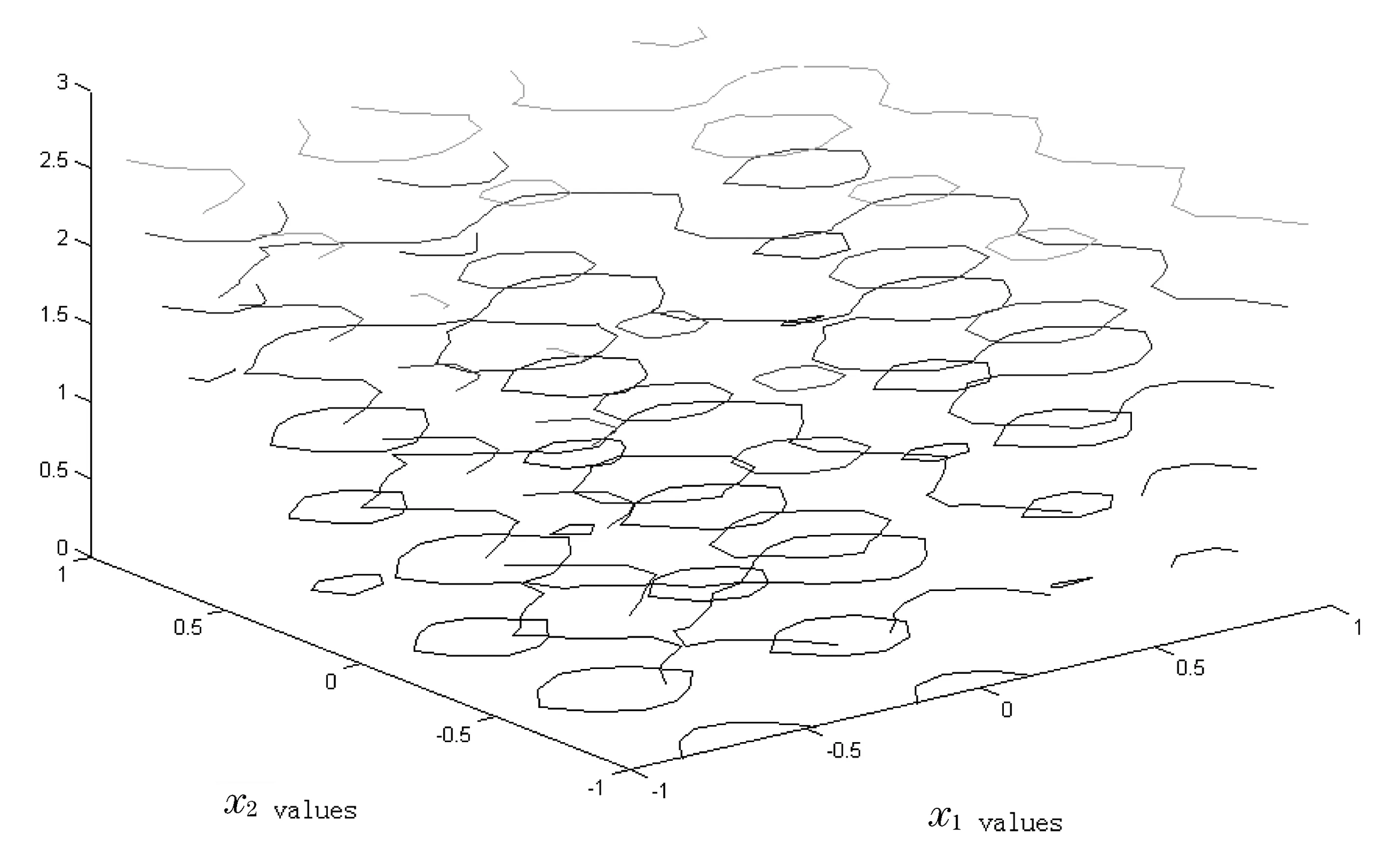
图4 函数u(x,y)的三维等高线图

通过图1至图4对函数u(x，y)从四个不同角度演示，学生可以感受到直观和抽象的过程. 三维图1符合视觉习惯最容易理解. 虽然等高线图2是二维图形比较抽象，但是其位置信息非常明确，定位性好. 图3不仅可以定位，而且表明了函数的确切趋势，其信息量比图2丰富. 图4给出了函数在空间中等高线，以了解函数值的空间分布.

3 教学思考

市场上还有许多其他最优化软件，如Lindo和Lingo等. 这些软件是工程设计和教学训练中的基本工具，是否能够熟练地掌握这些应用软件将影响到其他专业课的学习和潜力发挥.

虽然本文所选例子不是非常复杂，但通过该部分内容的课程设计，一方面可以让学生体会到准确找到我们需要的曲面上的最值点需要进行认真的有效的分析. 另一方面，可以培养学生对未知问题的分析能力，加强学生的动手能力的培养，提升学生的编程仿真能力. 事实上，学生只有在充分了解所讨论问题的性质和有一定的计算机编程基础的情况下才能根据问题本身的特点设计相应的高效搜索算法. 可视化的结果在引起学生好奇心的同时，展现了所研究问题的许多细节，也有助于学生兴趣的培养.

[参 考 文 献]

[1] 郭美荣，侴爱辉，夏德宏,等. 可视化教学法在实验教学中的应用[J]. 实验室研究与探索, 2012, 31(11): 128-130.

[2] 郝兴伟，龙世立，巩裕伟. 基于网络的计算机基础教学过程管理研究与实践[J]. 中国大学教学, 2010 (3):49-51.

[3] Nocedal J， Wright S J . Numerical Optimization[M]. Berlin：Spring-Verlag Press，1999.

[4] 博南J F, 夏皮罗A．最优化问题的扰动分析[M]．张立卫译.北京：科学出版社，2000.

[5] Boyd S, Vandenberghe L. Convex Optimization[M]. London：Cambridge University Press, 1999.