陈美霞，邓乃旗，张 聪，魏建辉

(华中科技大学 船舶与海洋工程学院,武汉 430074)

环肋圆锥壳为工程中常见结构。支撑水下航行体螺旋桨与轴系艉部结构常采用该结构形式。水下航行体主要噪声源之一为由桨的脉动力激起艇体艉部振动并辐射声而产生的结构振动噪声。为研究水下航行体振动噪声机理，本文针对截顶环肋圆锥壳在水中的振动特性，将螺旋桨脉动激励模拟为对圆锥壳施加纵向点激励，通过考虑圆锥壳在点力下受迫振动位移响应研究螺旋桨激起艇体振动机理，提出适合解决任意边界条件下水中环肋圆锥壳振动特性的计算方法。

锥壳在水中与流体耦合振动会改变其动力特性。由振动方程知，由于锥顶角的存在，锥壳半径随母线方向不断变化，使壳体本构方程出现拉弯耦合项，方程系数由圆柱壳时的常系数变为变系数，难于求其精确解。国内的研究主要集中于圆锥壳强度、稳定性、固有振动特性。王安稳等[1]提出关于圆锥壳轴对称变形的有矩理论方程。崔维成等[2]由旋转壳体的基本微分方程出发，重新推导圆锥壳应力计算精确解。崔维成等[3]将圆锥壳有矩问题求解的基本微分方程转换成二阶复常系数常微分方程式可用于圆锥壳边界效应。对圆锥壳振动分析研究尚少。骆东平等[4]用Flügge壳体理论及迁移矩阵法研究环肋圆锥壳自由振动。Crenwelge等[5]用能量法计算简支环肋圆锥壳自由振动。Tong等[6]用幂级数解各向异性圆锥壳自由振动。Caresta等[7-9]沿用文献[6]方法并考虑流体负载作用，研究水中圆锥壳、圆柱壳及锥柱结合壳在各种边界条件下的振动特性。Efraim等[10]采用幂级数法求解包括圆锥、圆柱、圆板在内的轴对称局部壳体固有频率。Leissa[11]用解析法、试验法分析锥柱壳的模态及振型。吴仕昊等[12-13]基于区域分解方法研究圆锥壳-圆柱壳-球壳组合壳体的固有振动。文献[10]仅考虑真空中壳体结构固有振动，未考虑流体负载影响，而文献[7]则未考虑环肋对壳体振动特性影响；为此，本文采用幂级数法与波传播法结合方法对水中环肋圆锥壳固有及受迫振动特性进行研究。幂级数法求解锥壳振动，用波传播法考虑分段等效圆柱壳上流体载荷，搜索水中复波数，用平摊法等效环肋，分析水流体负载、环肋、边界条件、半锥角及长度对振动特性影响。国内将该方法用于水中环肋圆锥壳振动特性研究尚少见。

1 水中环肋圆锥壳振动耦合方程求解

1.1 环肋圆锥壳运动方程

Flügge壳体理论描述的圆锥壳运动方程[14]为

(1)

(2)

(3)

式中：uc,vc分别为壳体中面沿x，θ方向位移；wc为壳体中面沿z方向法向位移，理论模型见图1；ρ为壳体密度；h为壳体厚度；α为半锥角；R为锥壳任意位置x处半径；R1，R2分别为锥壳小、大端半径；Nx,Nθ,Nθx,Nxθ,Qx,Qθ为锥壳内力项，见附录A。

本文将环肋圆锥壳等效为正交各向异性壳体，考虑等肋骨间距的环肋圆锥壳。环肋内力、内力矩表达式[15]为

(4)

(5)

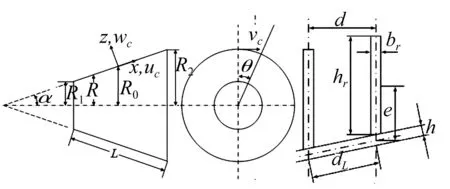
图1 圆锥壳几何模型与环肋尺寸示意图

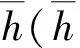
(6)

(7)

(8)

1.2 流体负载处理

由于圆锥壳各位置x处半径是变化的，求流体负载较难。故将圆锥壳划分成N段窄锥壳，每锥段等效成以锥壳分段平均半径为半径的圆柱壳，见图2。认为作用于每锥段的流体压力大小等同于作用于同长度的圆柱壳流体压力大小，通过该近似处理方法可得作用于圆锥壳的流体压力。

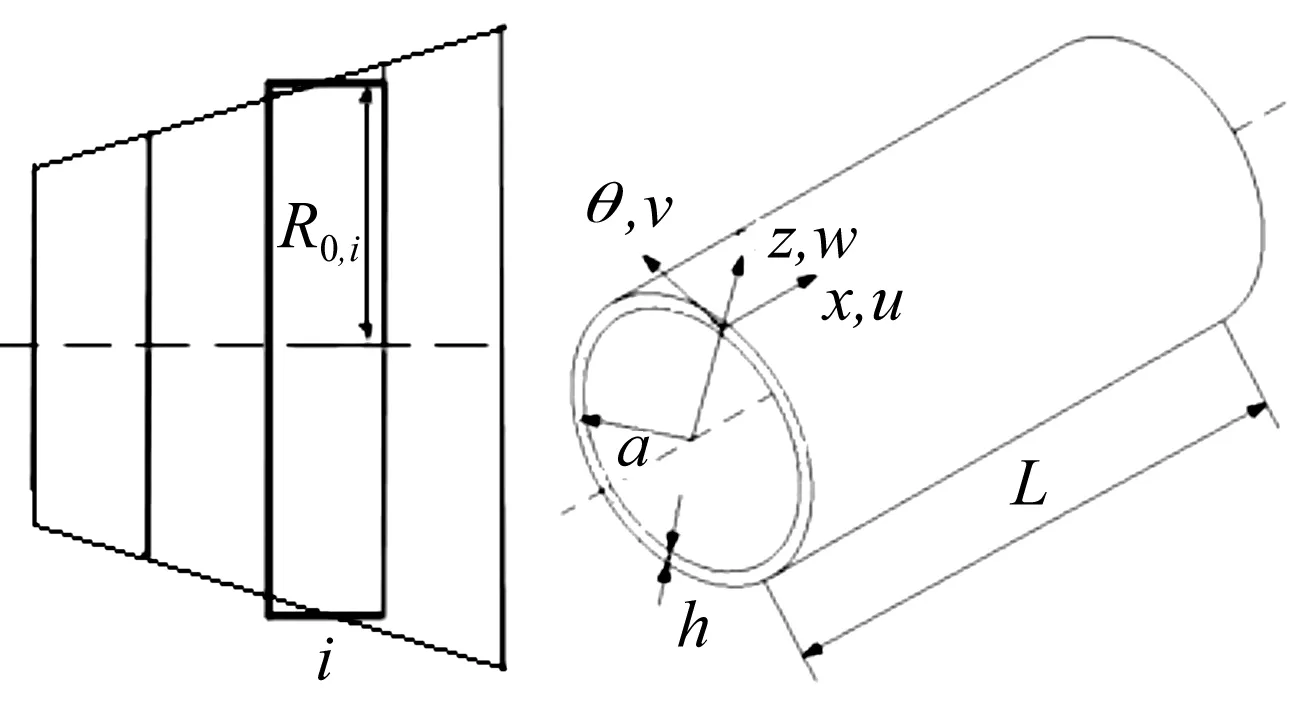
图2 锥壳分段与等效柱壳坐标系图

用Flügge方程描述分段圆柱壳运动方程为

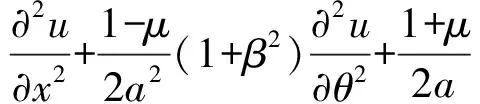
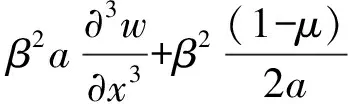
(9)

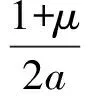
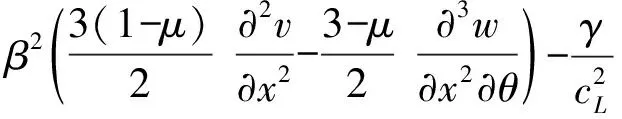
(10)

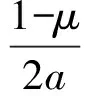
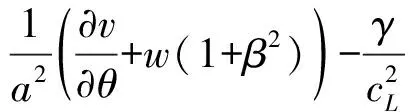
(11)

(12)

(13)

u(x,θ,t)=Uejknxcos(nθ)e-jωt

(14)

v(x,θ,t)=Vejknxsin(nθ)e-jωt

(15)

w(x,θ,t)=Wejknxcos(nθ)e-jωt

(16)

式中：U,V,W分别为轴向、周向、径向位移幅值。将通解代入式(9)～式(11)，得带U,V,W项的线性方程为

(17)

式中：Aij[7]为矩阵微分算子项。

对非齐次方程解，式(17)中矩阵行列式值必为0。展开行列式可得由kn，ω项构成的特征值方程。对每个ω，行列式值为关于结构波数kn的八阶控制方程。由于式(13)中汉克尔函数及贝塞尔函数的存在，特征方程为非线性，无法直接求解。因此须用数值方法求解kn。本文用搜索法。在无流体负载(Pa=0)情况下求解特征方程获得4对解。每对解中取1个解，该4个解作为流体负载的初始解。对实数解与虚数解，分别在实域、虚域范围内初始解附近搜索，获得能使控制方程为0的解。对复数解将初始解分解成实部、虚部，即kn=kre+jkim，其中kre为阻尼效应，kim为质量效应。控制方程也可分解为实部、虚部C=Cre+jCim，在初始解附近搜索同时使控制方程实部、虚部为0的解，即将控制方程C=0化为{Cre=0Cim=0}并求解。由于求解方法较复杂，可将流体负载逐步增加，先估计无流体负载解附近的带一半流体负载(0.5 Pa)的特征方程的解，再求解一半流体负载解附近的加载全部流体负载的复波数解。文献[14]给出每个锥壳分段的母线方向长度满足不等式Li≤2R0,iT%/sinα，其中T为分段系数，对同一锥壳模型，T保持不变。

1.3 连续条件

锥壳分段用力及位移连续条件连接，每锥段均需8个基本参数唯一描述，共需8N个基本参数确定整个锥壳振动，每两锥段间需满足位移、内力、内力矩连续条件。

位移连续条件：

(18)

力平衡连续条件：

(19)

式中：uc,i,vc,i,wc,iNx,i,Nxθ,iMx,i,Mxθ,iVx,i为每个锥壳第i分段处位移及内力；Ri为第i分段大径，i=1，2…N-1。

1.4 水中环肋圆锥壳自由、受迫振动求解

圆锥壳振动方程幂级数形式的一般解为

uc(x,θ,t)=uccos(nθ)e-iωt

(20)

vc(x,θ,t)=vcsin(nθ)e-iωt

(21)

wc(x,θ,t)=wccos(nθ)e-iωt

(22)

式中：n为锥壳周向模态数。

用幂级数表示位移分量：

(23)

(24)

(25)

将式(20)～式(25)代入式(6)～式(8)，可得序列数am，bm，cm的递推关系。据Flügge理论导出其表达式为

(26)

(27)

(28)

式中：Aai、Bai、Cai为相应项系数。据递推关系只需用8个基本参数a0,a1,b0,b1,c0,c1,c2,c3即可表示任意am(m≥2)，bm(m≥2)，cm(m≥4)。uc(x)，vc(x)，wc(x)可表示为

uc(x)=[u1(x)…u8(x)][a0a1b0b1c0c1c2c3]T

(29)

vc(x)=[v1(x)…v8(x)][a0a1b0b1c0c1c2c3]T

(30)

wc(x)=[w1(x)…w8(x)][a0a1b0b1c0c1c2c3]T

(31)

将内力、位移各项表示成关于a0,a1,b0,b1,c0,c1,c2,c38个未知系数的表达式。壳体两端边界条件与壳体分段间连续条件可组成矩阵方程Acxc=F，其中xc=[xc1T…xcNT]T;F为激励力列向量。

(32)

对第i分段，上式中位移、力连续条件矩阵为

位移连续矩阵：

(33)

内力连续条件矩阵：

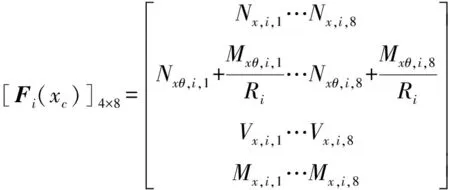
(i=1,2…N)

(34)

组合矩阵中，最初、最后两矩阵B1，BN为由锥壳两端边界条件决定。自由、简支、固支三种条件下矩阵为

自由端：

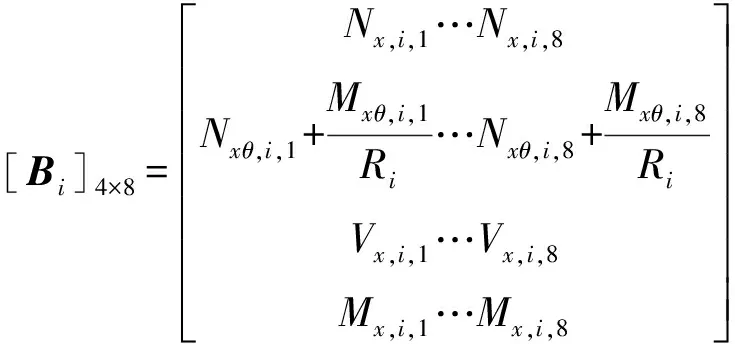
(i=1,N)

(35)

固支端：

(36)

简支端：

(37)

方程Acxc=F中激励力项F为0时，可求解环肋圆锥壳在水中的自由振动。令系数矩阵Ac的行列式值为0，即可求出固有频率ω。F不为0时，则可求解环肋圆锥壳在水中的受迫振动。激励力下壳体位移的频率响应函数可通过将激励力视为部分边界条件求得。对锥壳小大端自由、简支及固支情况，壳体在小半径端施加一沿母线方向点力F1或法向点力F2，平均幅值F0=1 N。见图3。

图3 圆锥壳点力受迫振动

求锥壳某点点力位移响应时用柱坐标系(x0c,θ,y0c)表达。其中y0c为锥壳任意位置半径方向长度坐标，θ为锥壳某截面周向角度坐标，x0c为锥壳轴向长度坐标。在柱坐标(x0c,θ,y0c)下，位于(x0,θ0,R(x0))处的点力可用δ函数表示(R(x0)为锥壳x0处半径)：

F(x,θ,t)=F0δ(x-x0)δ(θ-θ0)e-jωt

(38)

对壳体自由端，将激励力考虑成边界条件的一部分，在xi=x0处加载沿母线方向点力F1，该点边界条件中Nx的表达式为

Nx=F0δ(x-x0)δ(θ-θ0)e-jωt

(39)

代入x=x0，并对cos(nθ)在-π～π范围内积分，得：

Nx=εF0cos(nθ0)

(40)

当n为0时ε=1/2πR(x0)，n大于等于1时ε=1/πR(x0)。

同理，对法向激励F2，有

Vx=εF0cos(nθ0)

(41)

任意方向激励力均可分解到母线及法向求解。

对每个周向模态n，所有边界条件、连续条件及激励力均由矩阵方程Acxc=F表示，其中F为8N×1的力向量，只有一个非零项εF0。结果表示成一系列频率响应函数形式，该函数对每个频率、周向模态n求解方程Acxc=F，取前20个周向模态位移(n=0:20)叠加，即可求得锥壳面任点位移频率响应。位移响应在总体坐标系轴向x0c及径向y0c的分量为

ux0c,i=uc,icosα-wc,isinα

(42)

uy0c,i=uc,isinα+wc,icosα

(43)

2 数值计算与结果分析

为验证解析法的正确性，本文将解析法计算结果与有限元计算结果进行对比。圆锥壳参数：锥壳母线向长度L=8.9 m，轴线向长度L′=8.46 m。壳体厚度h=0.014 m，小端半径R1=0.5 m，大端半径R2=3.25 m，平均半径R0=1.875 m，半锥角α=18°，材料密度ρ=7 800 kg/m3，杨氏模量E=2.1×1011 N/m2，泊松比μ=0.3。在壳体表面均布环肋，肋厚br=0.014 m，肋高hr=0.04 m，肋间距l=0.21 m。流体声速cf=1 500 ms-1，流体密度ρf=1 000 kgm-3，结构损耗因子ηs=0.02。数值法用有限元软件ANSYS求解，壳体建模用shell63单元，环肋用beam188单元，外部流场用fluid30单元，吸声边界层用fluid130单元，共划分25万网格。

2.1 环肋圆锥壳固有频率

本文考虑三种边界条件的锥壳固有频率，即小端自由-大端自由(FR-FR)、小端自由-大端简支(FR- SD)、小端自由-大端固支(FR-CL)。计算每个周向模态n下最低固有频率。水中环肋圆锥壳在三种边界条件下的固有频率计算结果见图4。由图4看出，解析法与数值法计算三种边界条件下固有频率结果吻合较好，由此验证本文解析法求解水中环肋圆锥壳固有频率的正确性。较高周向模态出现误差主要源于环肋的平摊法等效。

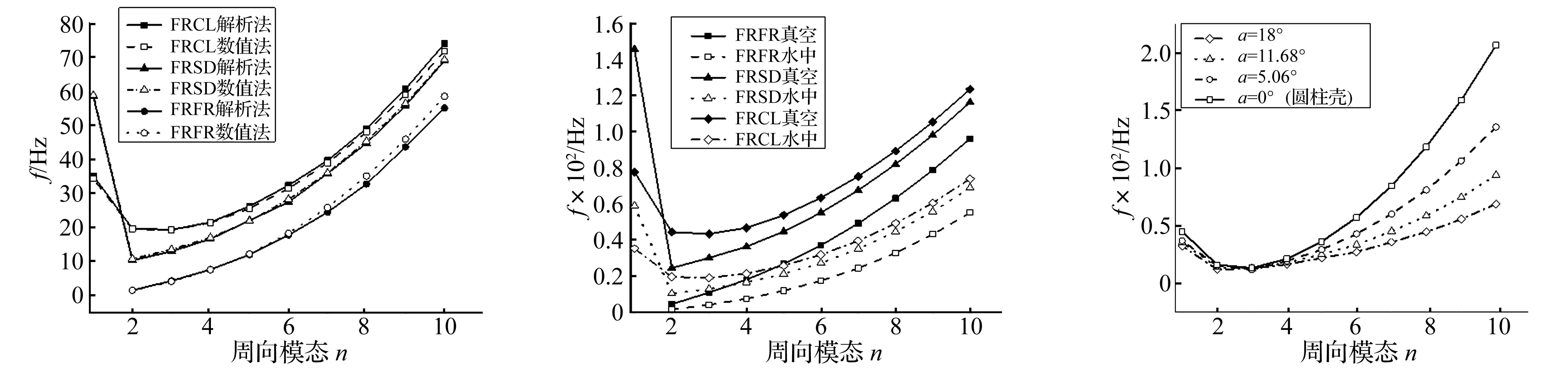
图4 三种边界条件下固有频率

图5为有无流体负载对圆锥壳固有频率影响对比。由图5看出，锥壳在水中的固有频率均小于在真空中固有频率。此因外部流体负载以附连水质量或阻尼形式作用于壳体振动法向，而附连水质量使壳体振动等效质量增加，故水中固有频率低于真空中固有频率。

为研究锥壳振动特有规律，考虑不同半锥角、壳体长度的锥壳固有振动特性。在锥壳结构参数基础上，不改变平均半径R0及轴向长度L′，仅改变半锥角α，两端简支条件下水中固有频率计算结果见图6。由图6看出，半锥角为0°的圆柱壳固有频率最高。随半锥角的减小，固有频率增大。n=1～3时半锥角影响不大，n=4～10时，半锥角越小，其变化对固有频率影响越大。半锥角减小时，锥壳结构沿轴向逐渐趋于对称，至圆柱壳时完全对称，锥壳刚度随之增大，模态数越高其固有频率也相应增大。

不改变锥壳平均半径R0及半锥角，仅改变轴向长度L′，两端简支条件下轴向长度对固有频率影响见图7。由图7看出，在相同半锥角及平均半径条件下，锥壳长度越短固有频率越高。而锥壳长度在周向模态数较低时影响亦较大。

图7 轴向长度L′对固有频率影响

2.2 点力下圆锥壳谐响应分析

为验证水中环肋圆锥壳受迫振动解析方法的正确性，用有限元软件ANSYS分析计算锥壳在水中的点力谐响应，并与解析法结果对比。理论计算模型见图3。圆锥壳小端为自由边界条件，端部加载沿母线方向单位点力F1或沿端部径向单位点力F3，大端固支约束。位移响应点取锥壳端部激励点A(0,0,0.5)或壳体中部点B(4.11,0,1.84)，取点轴向、径向位移幅值响应。用平摊法等效环肋，计算频率为1～250 Hz，计算F1激励下A点轴向响应，结果见图8，图中Re=10E-12 m/N。由图8看出，计算频率在1～116 Hz时解析法与有限元法峰值位置、位移幅值吻合良好，而在117～250 Hz时位移幅值误差较大，峰值位置出现偏移。说明平摊法等效环肋只适用较低频率范围。考虑工程实际中螺旋桨脉动产生的激励频率也在低频范围，本文取计算频率1～100 Hz，可保证计算的准确性。

图8 计算频率范围分析

图9、图10分别为F1，F3激励下环肋锥壳端点A及中间点B的轴向、径向位移幅值响应。由二图看出，① 解析法与有限元ANSYS计算结果吻合较好，验证了幂级数法的正确性。误差主要源于流体载荷的近似处理及平摊法等效环肋。② 水中响应峰值位置相对于真空峰值位置偏向低频，且响应幅值较小。此因为外部流体负载以附连水质量及阻尼形式作用于壳体的动响应，壳体振动阻尼增加，使壳体峰值响应幅值减小；附连水质量作用相当于振动时壳体质量增加，减小水中峰值对应的固有频率。

图11为环肋对水中锥壳响应影响。由图11知，环肋锥壳峰值小于不加肋骨峰值，且峰值位置相对偏向高频。此因为环肋以质量及刚度平摊方式作用于壳体，使壳体等效刚度及质量增加，而等效刚度增加的作用大于等效质量增加的作用，故峰值位置对应的固有频率变大。刚度增加限制壳体的振动位移，从而使峰值幅值变小。

图12为边界条件对水中环肋锥壳响应影响。锥壳小端为自由边界，大端分别为自由、简支、固支三种。由图12看出，频率较低时(1～30 Hz)，小端自由-大端简支与小端自由-大端自由边界条件响应曲线相近或重合；频率较高时(31～100 Hz)，小端自由-大端简支与小端自由-大端固支边界条件响应曲线相近或重合。研究表明，频率较低时锥壳轴向约束作用较大，而大端简支与自由两种边界条件均无轴向约束，故两种边界条件下曲线相近；频率较高时，锥壳径向、周向约束作用较大，大端简支与大端固支均对锥壳径向、周向有约束，故两种边界条件下曲线相近。

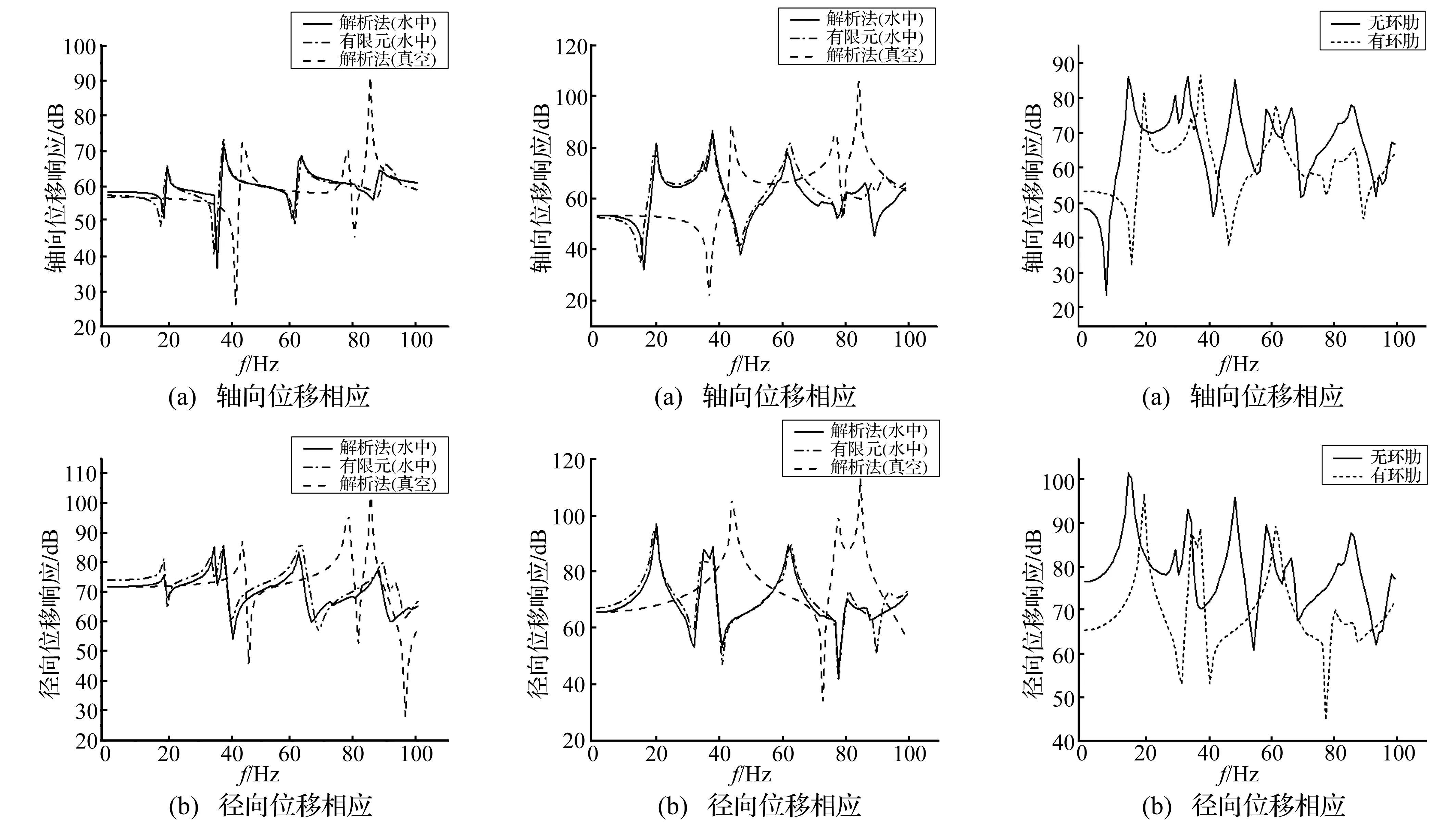
图9 F1激励下流体负载对环肋锥壳A点位移响应影响

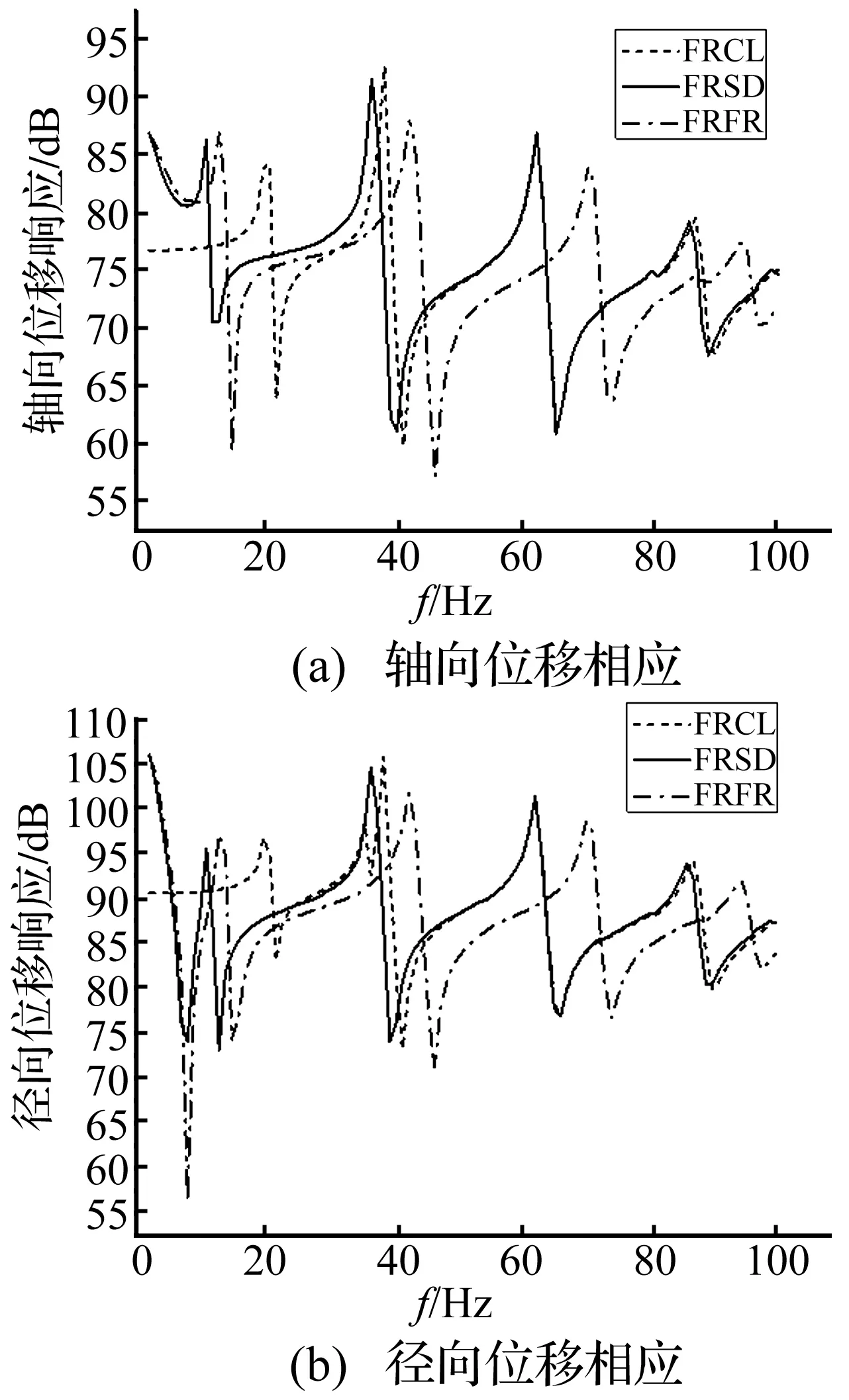
图12 F3激励下边界条件对水中环肋锥壳A点响应影响

以上结果已表明本文解析方法的正确性、适用性。该方法优点在于由壳体运动方程及力法角度分析壳体，能反应壳体的运动特性，采用幂级数法可灵活处理任意边界条件，且可用连续条件将不同壳体结构拼接计算组合结构。而传统有限元方法则将结构离散成微元，由动力学方程求解，无法反映壳体结构特性。幂级数法计算速度快，用ANSYS12.1计算水中环肋锥壳单个频率需15 min(2.8 GHz、8 G内存)，而用幂级数法在MATLAB2012b中编程计算仅需5 s，计算速度极大提升。处理流体负载方法简便，仅需改变流体参数及分段数，而有限元软件则需建流场单元，较耗时。故用幂级数法可通过修改结构及流体参数高效分析锥壳结构振动特性及规律，提取任意节点位移速度等信息，便于分析壳体声辐射，亦可将幂级数法编制计算软件，可更方便应用于工程实际中。

图9～图12中，Re=10E-12 m/N。

3 结 论

(1) 本文基于壳体振动的Flügge理论，采用幂级数法研究水中环肋圆锥壳固有振动及受迫振动特性。环肋采用刚度各向异性法，等效为壳体附加质量。通过将圆锥壳分段，将每段圆锥壳等效为圆柱壳考虑流体负载影响，采用搜索法搜获得水中复波数。数值法与本文幂级数法结果吻合良好，验证了本文计算方法的正确性。

(2) 通过对流体负载、环肋、边界条件、半锥角及轴向长度对锥壳固有振动、受迫振动特性影响研究，计算结果表明，流体负载以附连水质量、阻尼形式作用于壳体，会使锥壳固有频率降低、振动响应幅值减小；环肋主要以增加刚度形式作用于壳体，使壳体峰值对应的固有频率增高，且约束壳体振动，减小振动响应幅值；半锥角减小、轴向长度变短均会使固有频率增高；频率较低时锥壳以轴向约束作用为主，频率较高时以径向、周向约束作用为主。

[1] 王安稳,郭日修.圆锥壳方程的二次渐近解[J].海军工程学院学报,1993(2):1-8.

WANG An-wen, GUO Ri-xiu.Asymptotic solution of the second degree for the equation of conical shells[J].Journal of Naval University of Engineering, 1993(2):1-8.

[2] 崔维成,裴俊厚.圆锥壳的精确解与等效圆柱壳的解比较[J].船舶力学,2000,4(4):33-42.

CUI Wei-cheng, PEI Jun-hou.A comparison of equivalent cylinder solution with accurate solution for conical shells[J].Journal of Ship Mechanics, 2000,4(4):33-42.

[3] 崔维成,裴俊厚.具有薄壳理论同样精度的圆锥壳简化解[J].上海交通大学学报,2002,36(1):125-129.

CUI Wei-cheng, PEI Jun-hou.Simplified solution having the same accuracy as thin walled shell theory for conical shells[J].Journal of Shanghai Jiaotong University, 2002,36(1):125-129.

[4] 骆东平,赵玉喜.环肋圆锥壳自由振动特性分析[J].振动与冲击,1990,9(4):64-69.

LUO Dong-ping, ZHAO Yu-xi.Vibration characteristics analysis of ring-stiffened conical shells[J].Journal of Vibration and Shock, 1990,9(4):64-69.

[5] Crenwilge O E, Muster J R D.Free vibration of ring and stringer stiffened conical shells[J].J.Acoust.Soc.Am, 1969, 46(1):176-185.

[6] Tong L Y.Free vibration of orthotropic conical shells[J].International Journal of Engineering Science, 1993, 31(5): 719-733.

[7] Caresta M, Kessissoglou N J.Vibraion of fluid loaded conical shells[J].Acoustical Society of American, 2008,124(4): 2068- 2077.

[8] Caresta M, Kessissoglou N J.Free vibrational characteristics of isotropic coupled cylindrical-conical shells[J].Journal of Sound and Vibration,2010,329(6):733-751.

[9] Caresta M, Kessissoglou N J.Acoustic signature of a submarine hull under harmonic excitation[J].Applied Acoustics,2010, 71(1):17-31.

[10] Efraim E, Eisenverger M.Exact vibration frequencies of segmented axisymmetric shells[J].Thin-Walled Structures, 2006,44(3):281-289.

[11] Leissa A W.Vibration of shells[M].New York:American Institute of Physics, 1993.

[12] 吴仕昊,瞿叶高,华宏星.圆锥壳-圆柱壳-球壳组合结构自由振动分析[J].振动与冲击,2013,32(6):109-114.

WU Shi-hao, QU Ye-gao, HUA Hong-xing.Free vibration analysis of joined conical-cylindrical-spherical shells[J].Journal of Vibration and Shock,2013,32(6):109-114.

[13] 瞿叶高,华宏星,孟光,等.基于区域分解的圆锥壳-圆柱壳-圆锥壳组合结构自由振动[J].振动与冲击,2012, 31(22): 1-7.

QU Ye-gao, HUA Hong-xing, MENG Guang, et al.A domain decomposition method for free vibration analysis of a joined conical-cylindrical-conical shell[J].Journal of Vibration and Shock,2012,31(22):1-7.

[14] Caresta M.Structural and acoustic responses of a submerged vessel[D].Sydney: University of New South Wales,2009.

[15] Baruch M, Arbocz J, Zhang G Q.Laminated conical shells-considerations for the variations of the stiffness coefficients[C]//Proceedings of the 35th AIAA/ASME/ ASCE/ASC S.S.D.M.Conference, Hilton Head, SC: Delft University of Technology,1994:2506-2516.

附录A

(A1)

(A2)

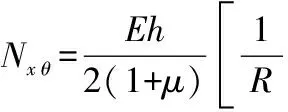
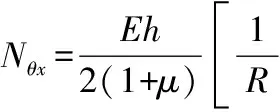
(A4)

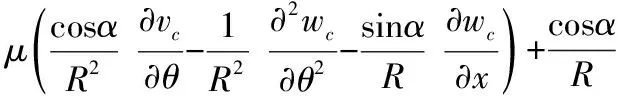
(A5)

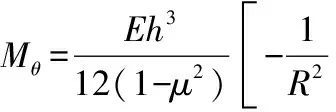
(A6)

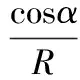
(A7)

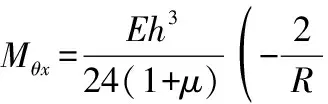
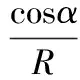
(A8)

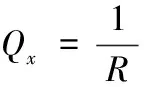
(A9)

(A10)

(A11)

式中：E,μ,h分别为杨氏模量、泊松比、壳体厚度。