董超雨，姜金平，张晓明

（延安大学数学与计算机科学学院，陕西 延安716000）

考虑下列粘性Cahn－Hilliard方程：

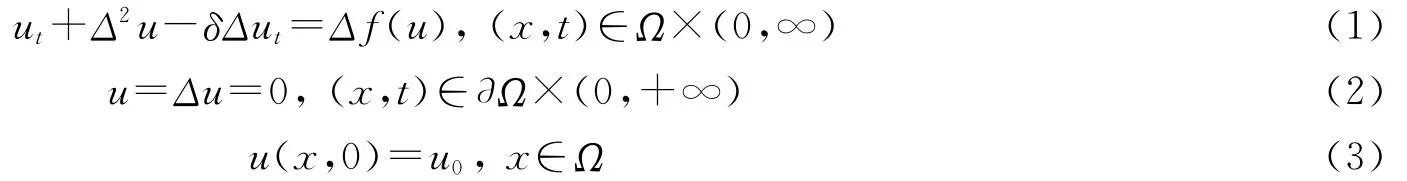
粘性Cahn－Hilliard方程是由Novick cohen等在1958年首次提出，用来描述带粘性的二物质相互扩散.许多学者对该方程进行了研究［1－3］.本文中对该方程在更高的正则性空间H2中的全局吸引子进行探究，同时参阅了其他方程的全局吸引子［4－5］，当δ＝0时，方程（1）是Cahn－Hilliard方程.Ω是R2（n≤3）中的有界集，非线性项f（u）满足如下条件：

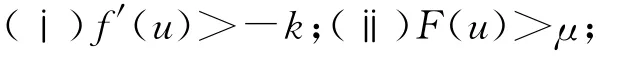
存在β，γ，正常数k1，k2且0＜β≤γ＜∞，使得：

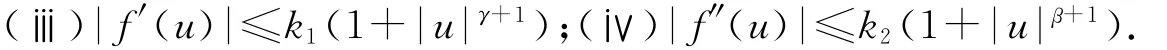
1 预备知识

本文中，c，c1，c2，…表示依赖于Ω 与n常数，分别记｜·｜p和‖·‖s表示Lp（Ω）和Hs（Ω）中的范数，特别地，｜·｜＝｜·｜2，‖·‖＝‖·‖2.令H＝L2（Ω），V＝H2（Ω）.定义Au＝Δ2u，则D（A）＝H1（Ω）∩H2（Ω）为A的定义域，显然，D（A）⊂V⊂H，并且嵌入是紧的.

定理1.1 对任意u0∈H，初值问题（1～3）式存在唯一解

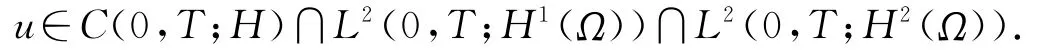
定理1.1的证明 利用Faedo－Galerkin逼近方法类似文献［5］可证.由定理1.1可定义一个连续算子半群S（t）：V→V，使得S（t）u0＝u.

定理1.2 以ρ0为半径的球Bρ0（0，ρ0）是 H1界吸收集，即 H1中的任何有界集B，存在t0，使得当t≥t0时，S（t）B⊂Bρ.

定理1.2的证明 用u与方程（1）式做内积，得：

带入（4）式及Poincare不等式｜u｜2≤λ｜ u｜2得：

由Gronwall不等式得：

半群S（t）的全局吸引子是一个紧的不变集A，通常方法由嵌入定理证明，运用文献［6］中一种新的验证紧性的方法，得到了预期的结果.

定义1.1［6］Banach空间X中的连续半群S（t）满足条件C，是指对任意ε＞0及X中任何的有界集B，存在t（B）＞0和一个有限维的子空间 H1，使得‖PS（t）B‖是有界的，并且‖（I－P）S（t）x‖≤ε，∀t≥t（B），x∈B，P：X X1是一个规范投影.

定理1.3［6］设S（t）是Hilbert空间X中的连续半群，如果下面条件成立；

1）S（t）在X中存在有界吸收集B⊂X；

2）S（t）满足条件C.

那么S（t）在X中存在全局吸引子A＝ω（B），且A吸引X中的一切有界集.

2 全局吸引子的存在性

2.1 H2有界吸收集的存在性 用v＝ut＋ε0u与方程（1）作内积，得：

由Poincare不等式得：

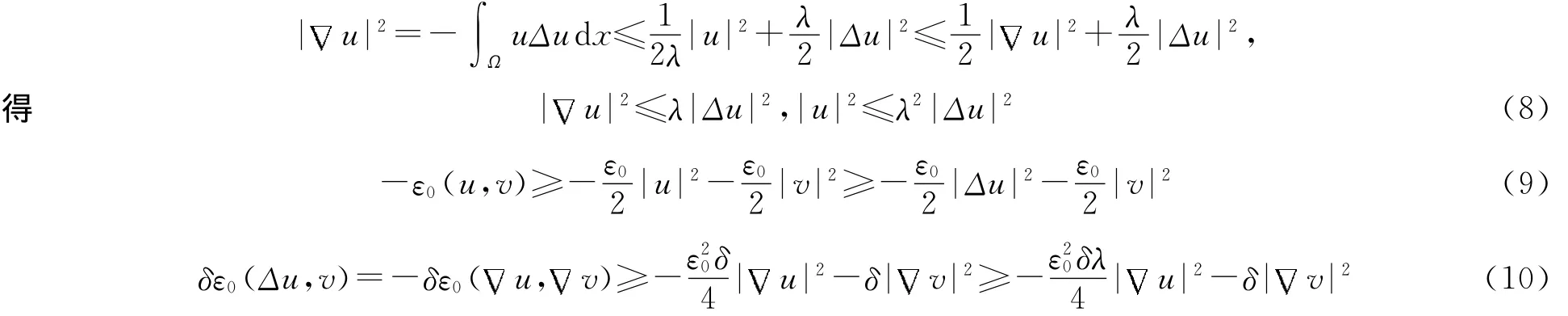
将（9～10）式代入（7）式得：

由Young不等式得：

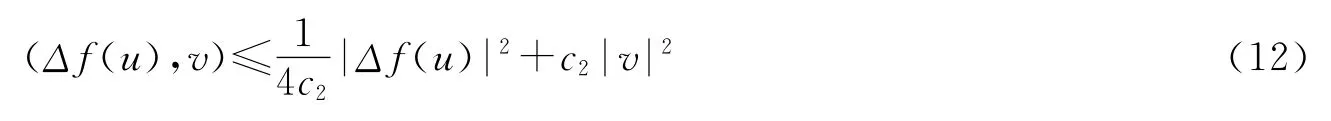
因为Δf（u）＝f″（u）（u）2＋f′（u）Δu，因 H1⊂L2，由（ⅳ）、（ⅲ）、sobolev嵌入定理及定理1.2得：

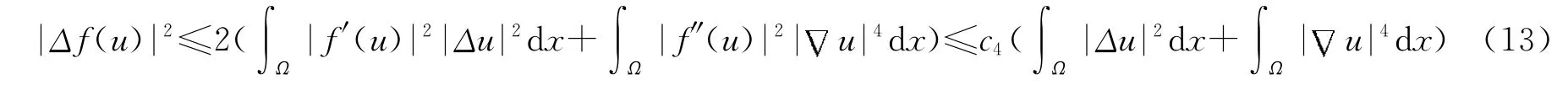
利用Gagliardo－Nirenberg不等式，得：

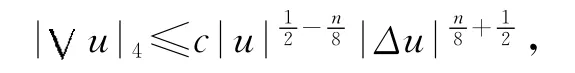
得

将上式代入（13）式得：

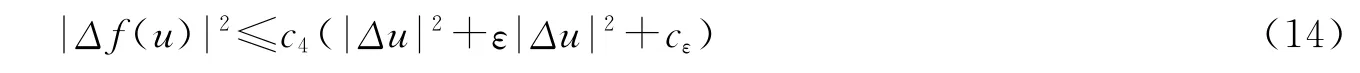
将（12～14）式代入（11）式得：

取适当的ε0，使得c7＞0，c8＞0，由Gronwall不等式得：

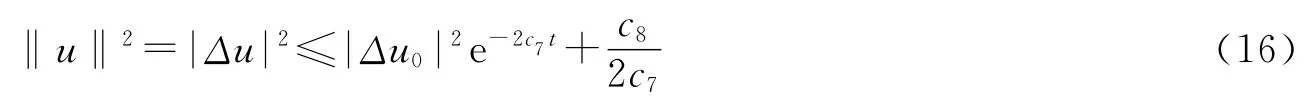
所以对任意‖u0‖≤R，存在，使得当t≥t1时

定理2.1 f满足条件ⅳ，以ρ1为半径的球Bρ1（0，ρ1）是问题（1～3）生成的解半群S（t）在 H2中的有界吸收集，即对H2中的任何有界集B，存在t1，使得当t≥t1时，S（t）B⊂Bρ1.

2.2 在H2中全局吸引子的存在性 记λ1，λ2，…，λk，…为A 的特征值，e1，e2，…，ek，…为对应的特征向量，当i→∞时构成了H2（Ω）的正交基，令Wm＝span｛e1，e2，…，em｝，W′＝W，记Pi：V→Wm为规范投影.

对∀u∈H，则有u＝u1＋u2，其中，用v2＝u2t＋ε0u2与方程（1）作内积，类似于（8～11）式的估计得：

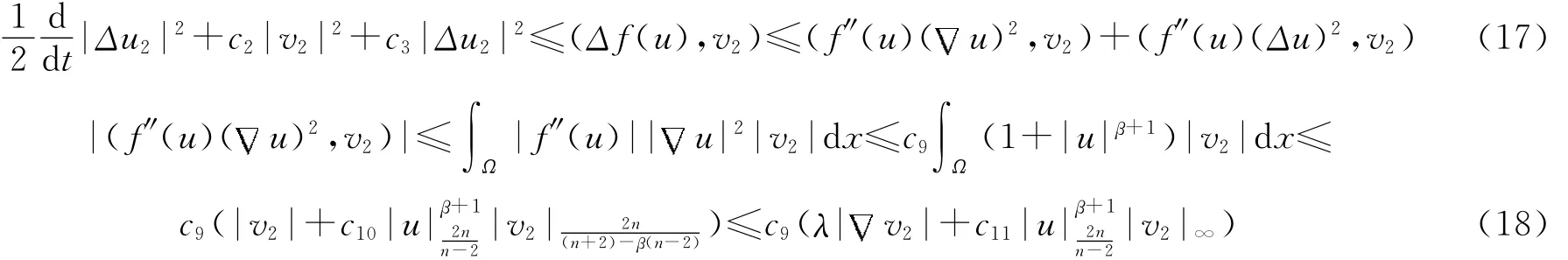
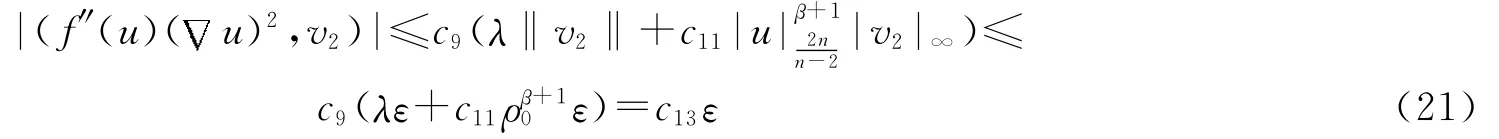
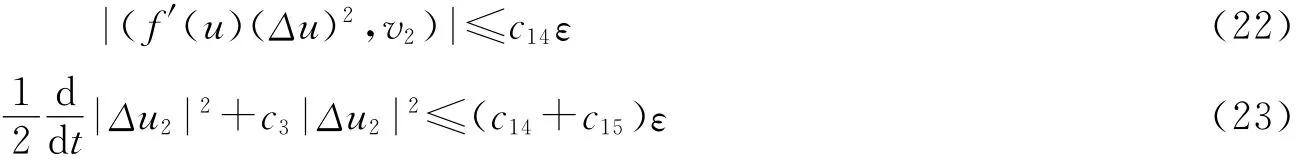
同理可得，取适当的ε0，使得c3＞0，由Gronwall不等式得：

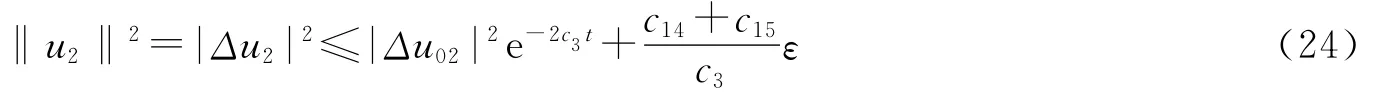
因此满足条件（ⅳ）、定理1.3、定理2.1，得：

定理2.2 设u0∈H2，初值问题（1）～（3）在H2中存在全局吸引子A＝ω（B），且A在H2的范数下吸引H2中的一切有界集.

［1］Liu Changchun，Yin Jingxue，Zhou Juan.A note on large time behaviour of solutions for viscous cahn－hilliard equation［J］.Acta Mathematica Scientia，2009B（5）：1－9.

［2］Elliott C M，Stuart A M.The viscous Cahn－Hilliard equation，PratⅡ：Analysis［J］.J Diff Eqns，1996，128：387－414.

［3］Hunag R，Yin J X.Global existence and blow－up of solutions to multi－dimensional（n≤5）viscous Cahn－Hilliard equation［J］.Northeast Math J，2005，21（3）：371－378.

［4］李洪涛，马闪.非经典抛物方程的一致吸引子［J］.兰州大学学报：自然科学版，2010，46（2）：71－75.

［5］Teman R.Infinite dimensional dynamical systems in mechanics and physics［M］.New York：Springer，1997.

［6］Ma Q F，Wang S H，Zhong C H.Necessary and sufficient conditions for the existence of global attractors for semigroup and application［J］.Indiana University Math J，2002，51（6）：1541－1559.