官春梅

(喀什师范学院数学系，新疆 喀什 844000)

0 引言

随机变量的随机比较在可靠性分析和保险精算理论中都有其重要的意义，近年来有许多关于非负独立随机变量的随机比较的成果.文献［1］研究了指数随机变量之和的随机比较，文献［2］给出了Gamma分布的随机变量之和的随机比较.Weibull分布是一种非常重要的寿命分布，在产品寿命和可靠性分析中有其重要意义.在保险精算中，Weibull分布也是极为重要的双参数生存模型，关于保险标底的风险和损失度量也常用到Weibull分布.而三参数Weibull分布是Weibull模型中对数据适应能力最强、拟合效果最好的.三参数Weibull分布是一种较为完善的分布，在拟合随机数据时有很大的灵活性，对不同形状的频率分布有很强的适应性.当形状参数取不同值时，它可以等效或接近于其他一些常用的分布［3-4］.关于重要概率分布的参数估计及参数特性在文献中设计［5-11］.本文讨论了三参数Weibull分布的随机变量之间的随机比较，给出了关于服从三参数Weibull分布的随机变量的顺序统计量的随机比较的结果.

设随机变量X服从三参数Weibull分布，其密度函数为

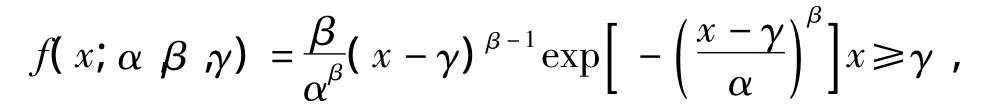
其中γ为位置参数，α＞0为尺度参数，β＞0为形状参数的分布函数(x≥γ)为

记 x～W(α，β，γ).

1 三参数Weibull分布的随机比较

定理1 假定 X 和 Y 是 Weibull分布随机变量，且 X ～W(α1，β1，γ1)，Y ～W(α2，β2，γ2).如果两分布的位置参数和形状参数相同，即 γ1=γ2=γ，β1=β2=β，则 X≤lrY 当且仅当α1≤α2.

证明 如果X和Y的概率密度函数分别为 f1(x;α1，β，γ)和 f2(x;α2，β，γ)，则有

X≤lrY⇔f1/f2关于X是减函数

从而由定理1容易得到下面的推论.

推论1 假定 X 和 Y 是 Weibull分布随机变量，且 X ～W(α1，β1，γ1)，Y ～W(α2，β2，γ2).如果两分布的参数满足:γ1= γ2，β1=β2，α1≤α2，则 X≤stY，X≤hrY.

定理2 假定 X 和 Y 是 Weibull分布随机变量，X ～W(α1，β1，γ1)，Y ～W(α2，β2，γ2).如果两分布的位置参数，即 γ1=γ2=γ，则 X≤stY 当且仅当α1≤α2，β1= β2.

证明 如果X和Y的分布函数分别为F(x)和G(x)，从而有

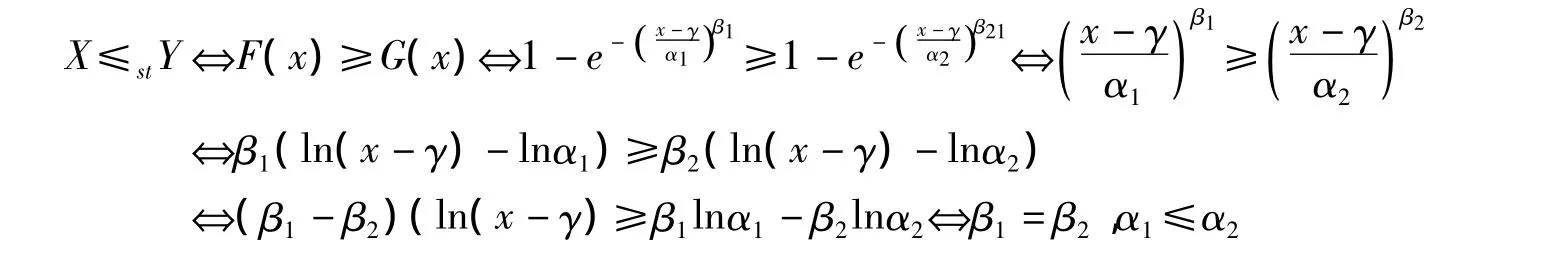
定理3 假定X 和Y 是服从Weibull分布的随机变量，即X ～W(α1，β1，γ1)，Y ～W(α2，β2，γ2).如果α1=α2β1=β2，γ1≤γ2，则 X≤stY.

3 Weibull分布次序统计量的随机比较

下面讨论独立但不同分布的三参数Weibull分布的次序统计量的随机比较.先给出一个概念.

引理1如果X是服从三参数的Weibull分布的随机变量，即X～W(α，β，γ)，X的危险率函数为R(t)，则

(1)当0≤β≤1时，R(t)是减函数;(2)当β≥1时，R(t)是增函数.

为了讨论方便，以下总假定随机变量X1，X2，…，Xn相互独立，随机变量Y1，Y2，…，Yn也相互独立，且Xi～ W(λi，β，γ)，Yi～ W(μi，β，γ)，i=1，2，…，n.X(i)为次序统计量，即

定理4 假设X1，X2(Y1，Y2)独立且服从三参数的Weibull分布，位置和形状参数分别为γ和β，尺度参数为 λ1，λ2(μ1，μ2)，且(λ1，λ2)≻(μ1，μ2).则

(1)当0≤β≤1 时，X(1)≥stY(1)，X(2)≥stY(2)，

(2)当 β≥1 时，X(1)≤stY(1)，X(2)≥stY(2).

证明:令函数

则Xi和Yi的分布函数分别为F(λit)和F(μit)，生成函数分别为=1－F(λit)和.故

所以 (1)当0≤β≤1时，

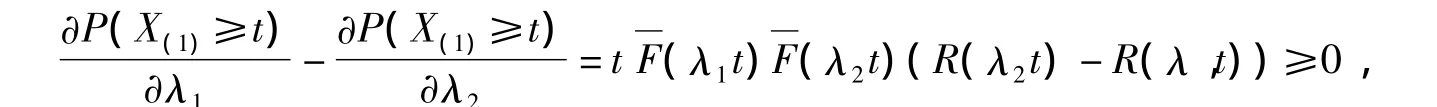
所以函数φ(λ)=P(X(1)≥t)是关于λ =(λ1，λ2)的Schur凹函数.又由于λ =(λ1，λ2)≻(μ1，μ2)=μ，故φ(λ)≥φ(μ)，即就是 P(X(1)≥t)≥P(Y(1)≥t).从而 X(1)≥stY(1).

(2)当 β≥1 时，函数 φ(λ)=P(X(1)≥t)是关于 λ 的 Schur凸函数.又由于 λ≻μ，故 φ(λ)≤φ(μ)，从而 X(1)≤stY(1).

下证只要β≥0，总有 X(2)≥stY(2).事实上，由于

所以函数 φ(λ)=P(X(2)≤t)是关于 λ =(λ1，λ2)的 Schur凹函数.又由于 λ =(λ1，λ2)≻(μ1，μ2)=μ，故φ(λ)≥φ(μ)，即就是 P(X(2)≤t)≥P(Y(2)≤t).从而 X(2)≥stY(2).

类似于定理4，同样可以证明下面的更一般的结论.

定理5 假设X1，X2，…，Xn(Y1，Y2…，Yn)独立且服从三参数的Weibull分布，他们的位置参数和形状参数分别为 γ 和 β，尺度参数为 λ1，λ2，…，λn(μ1，μ2，…，μn)满足 λ≻μ，λ =(λ1，λ2，…，λn)，μ =(μ1，μ2，…，μn).则:

(1)当0≤β≤1 时，X(i)≥stY(i)，i=1，2，…，n

(2)当 β≥1 时，X(1)≤stY(1)，X(n)≥stY(n).

［1］Chang，K.H.Stochastic orders of the sums of two exponential random variables［J］.Statist.Probab.Lett.，2001，51:389 ～ 396.

［2］Korwar，R.m.On stochastic orders for sums of independent random variables［J］.J.Multivariate Anal.，2002，80:344 ～357.

［3］Sun L H，Stochastic comparisons of order Statistics from Gamma distributions［J］.应用概率统计，2004，20(4):404 ～408.

［4］Pecaric，J.E.Convex Functions，Partial Orderings，and Statistical Application［M］.Academic Press，New York，1992.

［5］胡恩平，罗兴柏，刘国庆.三参数Weibull分布几种常用的参数估计方法［J］.沈阳工业学院学报，2000，(3):88～94.

［6］刘 菡，刘次华.定数截尾数据缺失场合下双参数指数分布参数的贝叶斯估计［J］.武汉大学学报(理学版)，2006，(3):286～290.

［7］徐 宝，于春艳，孙宪军.一种对称损失下Poisson分布参数倒数的Bayes估计［J］.吉林师范大学学报(自然科学版)，2006，(3):53～54.

［8］赵志文，刘银萍.具有部分缺失数据的两个幂分布总体参数的估计与检验［J］.吉林师范大学学报(自然科学版)，2008，(3):103～104.

［9］徐 宝，付志慧，张洪刚.贝叶斯框架下泊松分布参数倒数的估计［J］.吉林师范大学学报(自然科学版)，2010，31(1):57～58.

［10］杨瑞成，王国东.关于一种三参数Weibull分布的参数估计问题的研究［J］.鲁东大学学报(自然科学版)，2011，(3):203～206.

［11］刘银萍，马晓悦，赵志文.缺失数据场合泊松分布参数的贝叶斯估计［J］.吉林师范大学学报(自然科学版)，2012，33(3):13～15.