陈浩森， 李天匀， 朱 翔

(华中科技大学船舶与海洋工程学院， 湖北 武汉 430074)

引 言

对于浸没在流场中的无限长弹性薄圆柱壳，其频散特性一直是研究的热点，很多学者都已就此问题提出了自己的见解。Junger最早对浸没声场中的圆柱壳进行研究[1,2]，得出了附连水的存在大大降低了壳体的固有频率，并且主要影响低频振动的结论。Scott对水下无限长弹性圆柱壳自由波传播的频散特性方程作了深入研究[3]。他基于Love壳体理论和能量原理建立了耦合系统的频散方程，并用真空中相同的无限长圆柱壳的频散方程的解在复平面上通过迭代求得了水下圆柱壳的频散曲线，结束了前人用频散方程实部的根代替频散方程的根的历史，具有很高的理论价值。Guo推导出水下圆柱壳频散方程的近似解[4]，绘制了扭转波、压缩波以及弯曲波对应的频散曲线。左迎涛等人求取和分析了水下无限长弹性薄圆柱壳的频散特性曲线[5]，并与真空和空气中相同参数结构的特性作了对比。刘志忠在前人工作的基础上[6]，计入静水压力的影响，并研究了静水压力对耦合系统频散特性的影响。

在以往对流场-圆柱壳耦合系统的研究中，采用的流场大多为理想流场，针对声振问题建立的数学模型较简单。然而在实际情况中，流体必然存在粘性，仅在量级上不同。流体的粘性作用使流体中产生切向应力，并影响结构的振动特性和动力强度，进而对结构的振动能量流和声辐射特性产生影响。相对于理想流场中只存在纵波，粘性流场中既有纵波又有横波，加入粘性的影响势必会使流场与壳体结构的耦合变得更加复杂。忽略流体粘性固然可以使问题大大简化，但是考虑流体的粘性无疑会使建立的理论模型与实际情况更加接近，能更好地模拟真实情况。因此，研究中考虑流体粘性的影响是非常有价值的，为实际中的粘性流场-圆柱壳耦合系统的声振特性的研究提供了更充分的理论依据。本文的工作旨在定量分析流体粘性对结构波和流体声波的影响程度，这些目前尚无文献报道。

现今针对粘性流场-圆柱壳耦合系统的特性研究的相关文献较少。Yeh和Chen分析研究了双层同心圆柱壳-粘性流体耦合系统的动态性能[7]。Vollmann等采用Navier线弹性理论结合波传播方法来描述耦合系统[8]，导出了黏弹性介质的充液双层圆柱壳的频率与轴对称波型复波数之间的关系。Hasheminejad等把Havriliak-Negami模型应用于粘弹性材料动态的描述[9]，并与Donnell理论结合起来研究浸没在粘性和充有粘性液体无限长圆柱壳的自由振动和阻尼特性。Hasheminejad和Safari对浸没在粘性流体中有粘弹性覆盖层球壳和圆柱壳的声散射进行了研究[10]。Sorokin研究了加载了静态粘性可压缩流体的弹性板的自由波传播和衰减[11]，分析表明液体粘性对自由波存在不同程度的影响。Hu对一个充满粘性液体、径向极化、浸没在粘性液体中的压电球壳进行了轴对称振动的研究[12]，说明了在球壳中的液体对于浸没在液体中的球壳的振动有主导作用。这些文献的研究一方面表明流体粘性对声振特性存在影响，另一方面其研究方法有较好的借鉴作用。但是，部分前期文献更多是从流固耦合的角度分析粘性流场-圆柱壳耦合系统的振动，将流场介质认为是不可压缩的。当从声固耦合的角度分析耦合系统的声振特性时，由于声波的存在，流场中的介质是可压缩的，不可压缩粘性流体理论不再适用，需要寻找新的理论方法来描述声固耦合问题。论文首次开展粘性流场中圆柱壳结构的频散特性研究，建立了圆柱壳-粘性声场的声振耦合模型。

本文考虑薄圆柱壳壳体与由有粘、可压缩流体组成的流场之间的相互作用，把线性化的连续性方程、线性处理后的Navier-Stokes方程和小振幅波动下的状态方程结合起来得到了粘性流场中的声波波动方程，运用对矢量场的Helmholtz分解定理将波动方程中粘性流体的速度场分解为标量势和矢量势，根据波动方程解的假设形式得到粘性流场在柱坐标系下的速度和应力的表达式，进而根据声场与圆柱壳外表面的运动协调条件，从理论上首次建立了粘性流场-圆柱壳耦合系统的声振模型，提出了相应的数值计算方法，初步揭示了流体粘性对结构波和流体声波的影响，为进一步研究耦合系统振动能量流、声辐射特性以及水下精确NAH(近场声全息)成像打下基础。

1 理论模型

考虑壳厚为h、中面半径为R的无限长弹性薄圆柱壳浸没于粘性流体声介质中；以x，θ和r分别表示壳体的轴向、周向和径向；U，V和W表示壳体中面的轴向位移、周向位移和径向位移；n为周向模态阶数，如图1所示。

图1 圆柱壳坐标系和周向模态

1.1 壳体振动方程

假设圆柱壳为各向同性的弹性薄壳，其厚度h远小于其中面半径R。圆柱壳动力模型可用Flügge方程表达[6,13]

其中，

L33=1+K+Kλ4+2Kn2λ2+Kn4-Kn2-Ω2,

1.2 粘性流场动力方程

假设流场是由有粘、无旋、可压缩的正压流体组成的均匀、静止流场，其连续性方程、线性化Navier-Stokes运动方程和线性状态方程分别为[14]：

(2)

(3)

(4)

式中ρf为流体密度，uf为流场的速度分布，p表示声压，μ为剪切粘性系数，μb为膨胀粘性系数，cf为声传播速度。

根据Helmholtz定理，任何矢量场都能够表示成无旋和有旋分量的和

uf=▽φ+▽×ψ

(5)

式中φ为速度势的无旋分量，为标量，代表纵波(膨胀波)；ψ为有旋分量，为矢量，代表横波(剪切波)。

假设流体中的传播波是简谐波，则方程的解具有以下形式[10]

(6)

联立方程(2)～(6)，可以推导出标量势函数φ和矢量势函数ψ应分别满足以下方程：

在柱坐标下，方程(7)具有以下形式的解[15,16]：

(8)

根据柱坐标下的基本场方程，可以得到用势函数表达的流场三个方向速度的大小[17]

(9)

同样也可以得到流场三个方向应力的大小[17,18]

(10)

将式(8)分别代入上面两式并略去简谐项，所得结果见附录。

1.3 耦合系统的运动方程

通过波传播法推导所得的三向应力大小即为壳体方程中的粘性流体对薄壁圆柱壳在x，θ和r方向施加的等效载荷

(11)

这里要指出的是Px，Pθ和Pr的量纲取面载荷的量纲，而不是力的量纲。

根据壳壁外表面的运动协调条件，流场与圆柱壳在结合面三个方向的速度是连续的，即

(12)

联立方程(1)，(11)和(12)，即可得到耦合系统的运动方程

(13)

其中，

O12=0,

方程(13)有非零解的条件是系数矩阵的行列式为零，即为描述轴向波数kns与无量纲频率Ω关系的特征方程

(14)

从上式可知，根据给定的频率，可求得一系列的轴向波数，即可得到系统各支波的频散特性。

2 数值计算

耦合系统的特征方程是一个复平面上的高阶超越方程，必须采用数值方法来求解。本文采用的是Winding-Number围线积分法来求解其复根[19,20]。这些方程的解可按λ的值分为三类[3]：当λ为实数时，它表示沿圆柱壳轴向的传播波；当λ为纯虚数时，它表示近场衰减波；当λ为复数时，有两种情形：一种为Re(λ)±Im(λ)的形式，表示随传播距离呈指数衰减的耗散波；另一种为±Re(λ)+Im(λ)的形式，它必须成对出现，表示一对沿相反方向传播，而沿其中一个方向衰减的共扼衰减驻波。

取计算参数与文献[6]相同：壳体参数材料为钢，弹性模量E=2.1×1011N/m2，泊松比ν=0.3，密度ρs=7 850 kg/m3，厚径比为h/R=0.02。流体自由波传播速度cf=1 500 m/s，流体密度ρf=1 000 kg/m3。给定不同的无量纲频率Ω和周向波数n，求解频散方程即可得到相应的无量纲轴向波数λ。

2.1 对比与验证

理想流体是对实际问题的一种简化，忽略了流体的粘性，即其膨胀粘性系数μ和剪切粘性系数μb均为零，因而其中只存在纵波，也就是上述推导中与横波相关的势函数ψ为零。于是圆柱壳浸没在理想流体中时，其结合面的连续条件发生了变化，仅存在径向的速度连续。而将势函数ψ为零代入方程(9)会发现，在周向和轴向速度的表达式中仍然存在关于与纵波相关的势函数φ的项，与上述不符。描述粘性流场和理想流场的波动方程不仅仅是粘性系数上的差别，两种方法的思路和建立途径都是不一样的，直接将μ=μb=0代入耦合系统的频散方程中无法退化得到理想流体中的结果。当粘性流场中流体的膨胀粘性系数μ和剪切粘性系数μb取趋近于零的极小值而且结果收敛时，粘性所产生的影响变得极其微弱，流体可视为理想的。将μ=μb=10-10kg/m·s，μ=μb=10-12kg/m·s和μ=μb=10-15kg/m·s分别代入特征方程中并比较后可发现，当μ=μb=10-15kg/m·s时，计算结果趋于收敛。因此，选取周向模态数n=0，μ=μb=10-15kg/m·s时的计算结果与文献[6]中理想流体的相关计算结果进行比对，如图2所示。

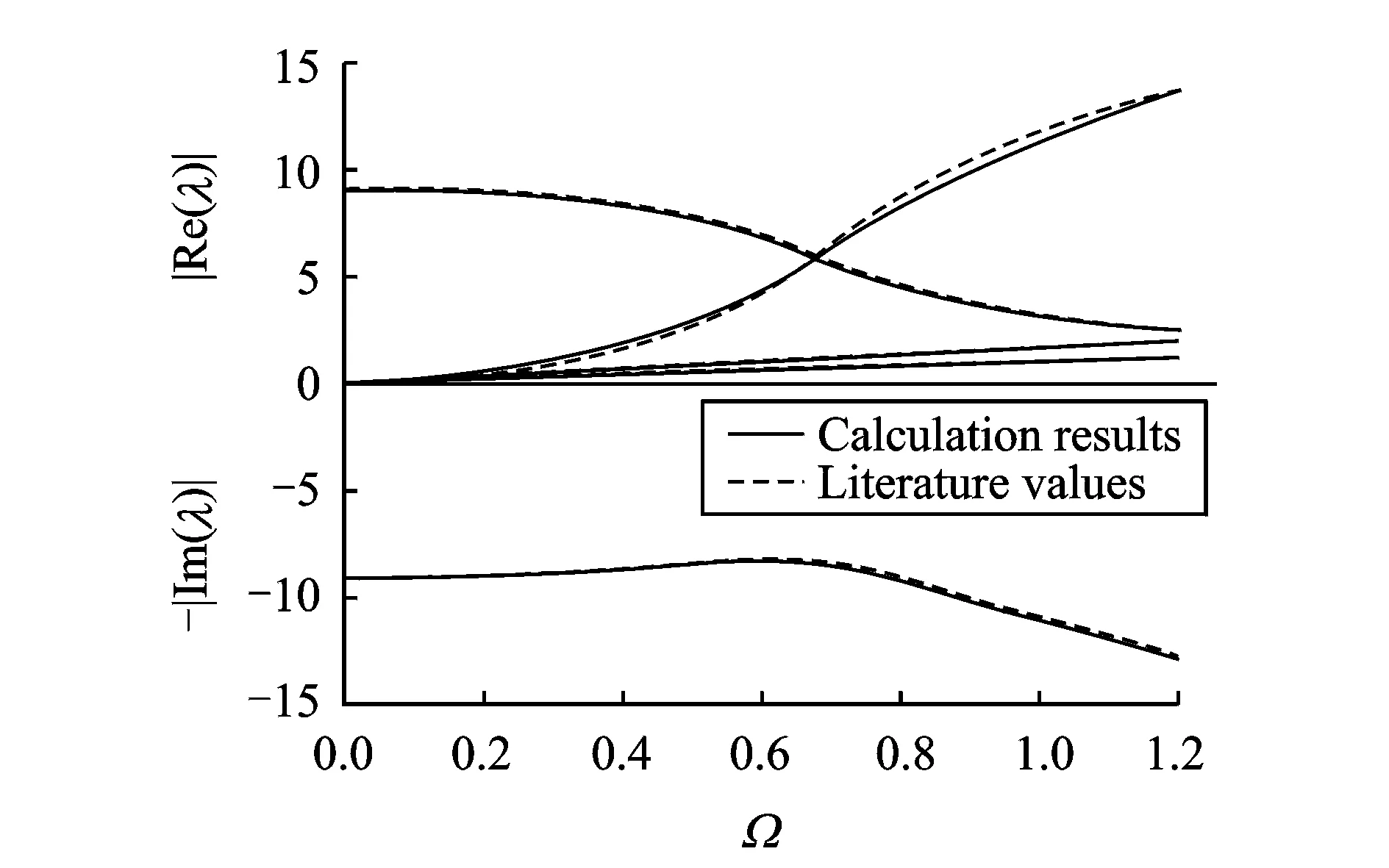
图2 计算结果与文献值的比较

图中横轴表示无量纲频率Ω，纵轴表示无量纲轴向波数λ，在横轴上方绘制λ实部的绝对值，横轴下方绘制其虚部绝对值的负值。由图可知，本文的计算结果与文献吻合较好，说明了本文方法的正确性和计算程序的可靠性。

2.2 耦合系统的频散曲线

为了分别研究剪切粘性系数μ和膨胀粘性系数μb对耦合系统频散特性的影响，取表1所示的3组数据进行对比研究，并分别标记为参数1、参数2和参数3[21]。需要说明的是，这里所选的参数1和参数3分别对应水和甘油的粘性系数。但是，水和甘油相比，在密度、声速等上都有较大的差距。如果单纯地拿出水和甘油作为介质进行对比分析，就引入了密度、声速等的变化带来的对频散特性的影响，不利于结论的得出。因此，为了能够更明确地说明流体粘性对耦合系统频散特性的影响，这里只选取两种介质的剪切粘性系数和膨胀粘性系数，其他计算参数均不变。

表1 剪切粘性系数μ和膨胀粘性系数μb的取值

将得到的结果绘成不同周向模态下耦合系统传播波的频散特性曲线，如图3～5所示，图中曲线上的数字为频散方程轴向波数解的序号s。

2.3 壳体中结构波的性质

从频散曲线可知，对于任一个周向模态，壳体中都存在三个传播波，分别对应于图中的s=1，s=2和s=3三条曲线。由上至下三个波的相速度在高频处分别接近于平板中的弯曲波，轴中的扭转波和平板中拉伸波的相速度。当n=0时，三支传播波总是出现在Ω=0处；随着n的增大，它们的起始频率也增大，且起始频率的大小与周向模态数成正比。此外，传播波s=1完全位于声速线以上，是亚声速波，不能向外辐射能量；传播波s=2和传播波s=3位于声速线以下是超声速波，可以向外辐射能量。当周向波数增大时，第一支波逐渐接近声速线，二者甚至会相交，反映出第一支波与流体的作用增强，甚至可能向外辐射能量。

图3 参数1下耦合系统的频散曲线

图4 参数2下耦合系统的频散曲线

图5 参数3下耦合系统的频散曲线

从图中发现，耦合系统中不仅存在着沿圆柱壳轴向的传播波，还存在着耗散波，某些周向模态下甚至会出现近场衰减波(将后两者统称为复数波，下同)，例如图3(a)中的曲线s=4就是周向模态n=0时系统中耗散波的频散特性曲线，而3(c)中的曲线s=4就是周向模态n=5时系统中近场衰减波的频散特性曲线。为了定性地说明壳体中衰减波的性质，将求得的轴向波数代回原方程(18)，定义特征向量：

(20)

(21)

它们表示对任一特定的波(n，s)，壳体三个方向上位移分量的比值，从而可以说明壳体运动是以轴向拉伸、周向扭转或者径向弯曲运动为主。

以参数3为例，将计算结果绘制成不同粘性系数下，耦合系统复数波的幅值比曲线，如图6所示。图中横轴表示无量纲频率Ω，纵轴表示特征向量Φns和Ψns，在横轴的上方绘制Φns的绝对值，横轴下方绘制Ψns绝对值的负值。

可以看出，对于耦合系统中的复数波，其波的数量会随着周向模态数的增大而增多，且不同的波的类型也不尽相同，有些波的类型甚至会随着频率的增加而发生变化。比如，当μ=0.000 984 kg/m·s，μb=0.002 5 kg/m·s，n=5，s=7时，刚开始时这支波以弯曲波为主，随着频率的增大，其扭转波的成分逐渐增大。此外，对于耦合系统而言，当衰减波是以扭转或拉伸波为主要成分时，其虚部相应很小；相应地，当弯曲波成为衰减波的主要成分时，其虚部相应很大。

3 流体粘性对耦合系统频散特性影响

参考文献[6]的数据，以n=0为例，将理想流场和粘性流场中耦合系统的频散特性曲线进行对比，如图7所示。

从图中可以看到，流体粘性对耦合系统频散特性的影响主要体现在波的起始阶段或者低频带，具体表现为以下三个方面：

图6 参数3下耦合系统复数波的幅值比曲线

图7 理想流场和粘性流场中耦合系统的频散特性曲线对比

1)流体粘性会导致传播波无量纲轴向波数λ的值减小，尤其体现在第一支上面。大部分复数波波数的实部基本都与粘性系数成正比，虚部则与之成反比。

2)流体粘性会使传播波的起始频率增大，并增加耦合系统中复数波的数量。而且，传播波的起始频率即为增加的复数波的截止频率。流体对流固耦合系统的影响主要集中在中低频段，并且考虑其粘性时增大了耦合系统的能量损耗。因此当频率较低时，某些波会因为粘性的影响无法向外传播，变成了近场衰减波，体现在图上即为传播波的起始频率增大和复数波的数量变多。

3)对于复数波s=4，粘性的增大使其无量纲轴向波数λ从复数变为虚数，即它从耗散波变为近场衰减波。

为了能够更直观地研究剪切粘性系数μ和膨胀粘性系数μb对耦合系统频散特性的影响，将三组不同参数下的计算结果进行比较，并引入相对变化参数Error的概念，将其定义为[22]：

式中i和j分别对应所选参数的编号。

以参数1和参数2为例，将上文计算得到的无量纲波数代入式(22)和(23)，绘制不同粘性系数时，相对变化参数的变化曲线，如图8所示。图中横轴表示无量纲频率Ω，纵轴表示相对变化参数Error，在横轴的上方绘制ErrorijRe的绝对值，横轴下方绘制ErrorijIm绝对值的负值。

分析图8中传播波的相对变化参数曲线，并结合相应的频散特性曲线可以发现，剪切粘性系数μ对耦合系统中传播波频散特性的影响主要体现在以下两个方面：

图8 相对变化参数曲线(参数1和参数2)

1)随着剪切粘性系数μ的增大，传播波s=1的起始频率会增大，而且其增大速度随着周向模态数n的增大而变慢，直至为零。

2)剪切粘性系数μ会影响传播波轴向波数的大小，而且大多数情况下，在波的起始阶段影响较大。当n=0时，三支传播波的相对变化参数Error最大约为0.045%；当n=1时，相对变化参数Error最大约为24%；当n=5时，相对变化参数Error最大约为2.7%。

而对于耦合系统中的复数波，剪切粘性系数μ的影响也体现在以下三个方面：

1)随着剪切粘性系数μ的增大，耦合系统中复数波的个数会增加；而随着周向模态数n的增大，其数量逐渐趋于一致。

2)随着剪切粘性系数μ的增大，复数波s=5的截止频率会增大，而且其增大速度会随着周向模态数n的增大而变小，直至为零。

3)剪切粘性系数μ会影响复数波轴向波数的大小，而且对复数波s=4的影响相对较大。当n=0时，复数波实部的相对变化参数ErrorRe最大约为5.3%，虚部的相对变化参数ErrorIm最大约为1.7%；当n=1时，其实部的相对变化参数ErrorRe最大约为0.027%，虚部的相对变化参数ErrorIm最大约为0.022%；当n=5时，其实部的相对变化参数ErrorRe最大约为0.11%，虚部的相对变化参数ErrorIm最大约为0.037%。

膨胀粘性系数μb对耦合系统中波的频散特性的影响，可以通过观察图11中的相对变化参数曲线，并结合相应的频散特性曲线来得到，主要体现在两个方面：

1)对于传播波而言，膨胀粘性系数μb的影响主要集中在s=1这支波上。随着膨胀粘性系数μb的增大，仅传播波s=1的起始频率在周向模态数n=5时出现增大的现象。膨胀粘性系数μb会影响传播波轴向波数的大小，且其相对变化参数Error的最大值基本出现在无量纲频率Ω=2左右的位置。当n=0时，三支传播波的相对变化参数Error最大约为25.1%；当n=1时，相对变化参数Error最大约为11.7%；当n=5时，相对变化参数Error最大约为24.9%。

2)至于复数波，随着膨胀粘性系数μb的增大，仅复数波s=6的截止频率在周向模态数n=1时出现增大的现象。膨胀粘性系数μb会影响复数波轴向波数的大小，且其相对变化参数Error的最大值基本出现在无量纲频率Ω=2之前的频段。当n=0时，复数波实部的相对变化参数ErrorRe最大约为2.25%，虚部的相对变化参数ErrorIm最大约为0.72%；当n=1时，其实部的相对变化参数ErrorRe最大约为72%，虚部的相对变化参数ErrorIm最大约为7.42%；当n=5时，其实部的相对变化参数ErrorRe最大约为73%，虚部的相对变化参数ErrorIm最大约为1.3%。

4 结 论

本文首先推导出粘性流场中无限长圆柱壳耦合系统的动力方程和特征方程，然后运用数值方法求解，最终得到其频散特性曲线。通过对粘性流场中无限长薄圆柱壳频散特性的分析，并结合复数波的幅值比曲线以及无量纲轴向波数的相对变化参数曲线，可以得到以下结论：

1)对于耦合系统而言，当衰减波是以扭转或拉伸波为主要成分时，其虚部相应的很小，这很小的虚部也极有可能是由占很小成分的弯曲波所产生的。虚部很小表明了其与流场进行能量交换的能力也较弱。相应地，当弯曲波成为衰减波的主要成分时，其虚部相应很大，与周围流场之间的能量交换也较强。

2)剪切粘性系数μ的增大会带来耦合系统中复数波个数的增加，膨胀粘性系数μb则不会。

3)剪切粘性系数μ的增大会带来传播波(主要体现在s=1这支波上)起始频率和复数波截止频率的增大，而且其增大速度会随着周向模态数n的增大而变小，直至为零。膨胀粘性系数μb的增大则仅会使传播波s=1的起始频率在周向模态数n=5时和复数波s=6的截止频率在周向模态数n=1时出现增大的现象。导致这一现象的原因可能是流体对耦合系统振动特性的影响主要集中在低频，以及流体粘性的存在使得耦合系统的能量损耗。

4)剪切粘性系数μ和膨胀粘性系数μb都会影响耦合系统中各支波轴向波数的大小。相对而言，膨胀粘性系数μb对轴向波数的改变更为明显，其相对变化参数的最大值可达73%。

5)剪切粘性系数μ和膨胀粘性系数μb改变所引起的相对变化参数，其峰值大部分都位于波的起始阶段或者低频带，也就是说流体粘性对耦合系统频散特性的影响主要集中在波的起始阶段或者低频带。

需要指出的是，本文用来分析圆柱壳体结构振动的Flügge薄壳理论是基于Love-Kirchhoff假设的，忽略转动惯量、横向剪切变形和横向挤压，仅适用于中低频和小的厚度半径比的情况，因此本文的计算结果同样仅适用于中低频和小的厚度半径比的情况。

参考文献：

[1] Junger M C. Radiation loading of cylindrical and spherical surfaces[J]. Journal of Acoustical Society of America, 1952,24(3)：288—289.

[2] Junger M C. Vibrations of elastic shells in a fluid medium and the associated radiation of sound[J]. Journal of Applied Mechanics, 1952,19(2)：439—445.

[3] Scott J F M. The free modes of propagation of an infinite fluid-loaded thin cylindrical shell[J]. Journal of Sound and Vibration, 1988,125(2)：241—280.

[4] Guo Y P. Approximate solutions of the dispersion equation for fluid-loaded cylindrical shells[J]. Journal of the Acoustical Society of America, 1994,95(3)：1 435—1 440.

[5] 左迎涛,张小铭,徐慕冰.流体声介质中无限长薄圆柱壳的频散特性[J].华中科技大学学报,1997,25(6)：37—39.Zuo Yingtao, Zhang Xiaoming, Xu Mubing. Dispersion characteristics of an infinite thin cylindrical shell immersed in acoustic medium[J]. Journal of Huazhong University of Science and Technology, 1997,25(6)：37—39.

[6] 刘志忠.静压条件下圆柱壳-流场耦合系统振动功率流和声辐射特性研究[D].武汉：华中科技大学,2009.Liu Zhizhong. Characteristics of power flow and sound radiation in cylindrical shell-fluid system considering hydrostatic pressure[D]. Wuhan: Huazhong University of Science and Technology, 2009.

[7] Yeh T T, Chen S S. Dynamics of a cylindrical shell system coupled by viscous fluid[J]. The Journal of the Acoustical Society of America, 1977,62(2)：262—270.

[8] Johannes Vollmann, Jürg Dual. High-resolution analysis of the complex wave spectrum in a cylindrical shell containing a viscoelastic medium[J]. The Journal of the Acoustical Society of America, 1992,102(2)：909—920.

[9] Hasheminejad S M, Shahsavarifard A, Shahsavarifard M. Dynamic viscoelastic effects on free vibrations of a submerged fluid-filled thin cylindrical shell[J]. Journal of Vibration and Control, 2008,14(6)：849—865.

[10] Hasheminejad S M, Safari N. Acoustic scattering from viscoelastically coated spheres and cylinders in viscous fluids[J]. Journal of Sound and Vibration, 2005,280(1/2)：101—125.

[11] Sorokin S V, Chubinskij A V. On the role of fluid viscosity in wave propagation in elastic plates under heavy fluid loading[J]. Journal of Sound and Vibration, 2008,311(3/5)：1 020—1 038.

[12] Hu Juxi, Qiu Zhiping, Su T C. Axisymmetric vibrations of a viscous-fluid-filled piezoelectric spherical shell and the associated radiation of sound[J]. Journal of Sound and Vibration, 2011,330(24)：5 982—6 005.

[13] Д Д 朗道,E M 栗弗席兹著.连续介质力学[M].彭旭麟,译.北京：高等教育出版社,1958：59—62,110—113.Landau L D, Ginzburg V L, Peng Xulin. Mechanics of Continuous Media[M]. Beijing: Higher Education Press, 1958：59—62,110—113.

[14] Hasheminejad S M, Geers T L. Modal impedance for two spheres in a thermovicous fluid[J]. Journal of the Acoustical Society of America, 1993,94(4)：205—214.

[15] Morse P M, Ingard K U. Theoretical Acoustics[M]. New York: McGraw-Hill, 1968：179—180.

[16] 何祚墉.水动力的波动问题[M].北京:国防工业出版社,1983：124—125.He Zuoyong. Hydrodynamic Wave Propagation Problems[M]. Beijing: National Defence Industry Press, 1983：124—125.

[17] Lin W H, Raptis A C. Acoustic scattering by elastic solid cylinders and spheres in viscous fluids[J]. Journal of the Acoustical Society of America, 1983,73(3)：736—748.

[18] Lin W H, Raptis A C. Sound scattering from a thin rod in a viscous medium[J]. Journal of the Acoustical Society of America, 1986,79(6)：1 693—1 700.

[19] Brazier-Smith P R, Scott J F M. On the determination of the roots of dispersion equations by use of winding-number integrals[J]. Journal of Sound and Vibration, 1991,3(2)：503—510.

[20] Ivansson S, Karasalo I. Computation of modal wavenumbers using an adaptive winding-number integral method with error control[J]. Journal of Sound and Vibration, 1993,l(4)：173—180.

[21] Vargaftik N B. Handbook of Physical Properties of Liquids and Gases[M]. Berlin: Springer, 1983：689—690.

[22] Li Xuebin. Study on free vibration analysis of circular cylindrical shells using wave propagation[J]. Journal of Sound and Vibration, 2008,311(3/5)：667—682.