闫爱民， 胡建华

（上海理工大学理学院，上海 200093）

根系在李理论的研究中起着极其重要的作用，根系中有两种重要的关系：偏序关系和正交关系.对于型An（n≥1）的根系，文献［1］将正根之间的这两种结构完全体现在一个n＋1阶的严格上三角矩阵上，这里只需矩阵的（i，j）位置表示根α＝εi－εj，其中，εi＝（0 … 0 1 0 … 0 ）是n＋1维单位向量.α≻β当且仅当α在β的右方、正上方；若存在某个i，划去第i行第i列后也划去了α与β，则α与β不正交，否则α与β正交.例A4中，正根αi＝εi－εi＋1，（i＝1，2，3，4），αi＋…＋αj＝εi－εj（1≤i＜j≤4）.用5阶矩阵表示为

与α2＋α3正交的根有α1＋α2，α3＋α4，α1＋α2＋α3＋α4

对于型E的根系，哈斯图很好地描述了它的偏序关系，但正交关系就不能表现出来.本文拟将具体地研究型E7的根系的性质，建立E7的根系到有限域上向量空间的单射，用分层的手段讨论E7的根系的偏序关系和正交关系.

设ℝn为实数域上n维欧氏空间，（，）表示内积，对∀α∈ℝn，对应一个反射σα.对任意β∈ℝn，σα简记为〈β，α〉，则σα（β）＝β－〈β，α〉α.

设Δ⊂ℝn是一个秩为n的根系，Π＝为Δ的基础根系，ℤ表示整数集.对于∀β∈Δ，可表示成若存在某个ki＞0（或ki＜0），就称β为正根（或负根），称为β的高度.Δ＝Δ＋∪Δ－，Δ＋＝－Δ－，其中Δ＋（Δ－）是Δ的所有正（负）根的集合.记Dyn表示Δ的Dynkin图，Dyn的顶点为v1，…，vn，它们对应单根α1，…，αn.

定义1［1］若Δ中所有根的长度相等，则称Δ为等长根系.此时∀β∈Δ，（β，β）＝2.

显然型An（n≥1），Dn（n≥4），E6，E7，E8的不可约根系为等长根系，且当Δ是可约的等长根系时，其Dynkin图的每一个连通子根系为型A，D，E的.

定义2［2］不可约根系Δ的最低根称为仿射根，记为的Dynkin图中添加仿射顶点得到的新图称为仿射Dynkin图，其中仿射顶点对应仿射根

下文中的Δ皆表示等长根系，可以是可约的.Λ＝ℤΔ表示由Δ，ℤ－张成的格.

性质1［3］对∀α，β∈Δ且α≠±β，有〈β，α〉

性质2［3］Δ＋是一个偏序集.对β，β′∈Δ＋，β≻β′当且仅当β－β′是正根之和.

性质3［4］α，β∈Δ，α＋β∈Δ当且仅当〈α，β〉＝－1；α－β∈Δ当且仅当〈α，β〉＝1.

性质4［4］若Δ是可约的且Δ＝Δ1∪Δ2，则对于∀α∈Δ1，β∈Δ2，〈α，β〉＝0.

为方便约定D2＝A1×A1，D3＝A3，E3＝A2× A1，E4＝A4，E5＝D5.

1 根系到有限秩自由模的单射

设p≥2是正整数，设V是ℤ／p上的有限秩自由模，V上有一个对称双线性型（·｜·），且其在ℤ／p上取值.设Γ＝｛x∈V＼｛0｝｜（x｜x）＝2｝.

假设Γ有一个子集S＝｛a1，a2，……，an｝满足以下条件：

a.S中元素两两不同；

b.（αi｜αj）＝〈αi，αj〉（modp），

这里S中元素两两不同是必要的，否则如当p＞3，〈α1，α2〉＝－1时，（a1｜a2）＝〈α1，α2〉（modp）＝2（modp），（a1｜a2）＝〈α1，α2〉（modp）＝－1（modp）.

若a1＝a2，则有（a1｜a1）＝2（modp）＝（a1｜a2）＝－1（modp），2＝－1显然矛盾.

显然，通过自然扩展映射αiaai可得到映射

引理1 如果β，β′∈Λ，那么（f（β）｜f（β′））＝〈β，β′〉（modp）.

证明 由f的定义和内积的双线性，显然.

推论1 若β≠±β′∈Δ，则〈β，β′〉＝0当且仅当（f（β）｜f（β′））＝0.

证明 因为β和β′是等长根系的根，〈β，β′〉∈｛－1，0，1｝，所以

〈β，β′〉＝0⇔〈β，β′〉＝0（modp）⇔（f（β）｜f（β′））＝0.

现在将f的定义域作以下限制：当p＞2时，定义域为Δ；当p＝2时，定义域为Δ＋.

对β∈Δ，记

引理2 当p＝2时，a.若O（β）＝Δ当且仅当β所在的不可约子根系为型A1的；

b.若O（β）≠Δ，则Δ＼O（β）的元只可能属于Δ的包含β不可约子根系中.

证明 a.必要性：当β所在的不可约子根系为型A1时，此子根系只有根｛±β｝，且此时β与其它子根系中的所有元素都垂直，因此对∀γ∈Δ＼｛±β｝有〈β，γ〉＝0，即O（β）＝Δ.

充分性：若O（β）＝Δ，且β所在的不可约子根系不是型A1的，则此子根系中至少存在α使得〈β，α〉≠0，与O（β）＝Δ矛盾.

b.若O（β）≠Δ，一定存在α∈Δ＼O（β）使得〈β，α〉≠0，α，β属于同一个不可约根系中.若Δ＼O（β）的元素属于Δ的多个不可约子根系，则一定存在α∈Δ＼O（β）与β不在同一不可约子根系中，则〈β，α〉＝0，α∈O（β），矛盾.所以Δ＼O（β）的元素只可能属于Δ的包含β不可约子根系中.

引理3 当p＝2时，对β∈Δ，a.若Δ是型A2的，则O（β）＝｛±β｝；

b.若Δ是型Ak（k≥4），E6，E7，E8的，则O（β）分别是型Ak－2×A1，A5×A1，D6×A1，E7×A1的，且β属于型A1的子根系中；

c.若Δ是型Dk（k≥3）的，则O（β）是型Ak－2× A1×A1，且β属于型A1的子根系中.

证明 这里只需根据Δ型逐一验证即可.

定理1 a.当p＞2时，f：Δ→V是单射，它的像位于Γ内；

b.当p＝2时，f：Δ＋→V是单射，它的像位于Γ内.

证明 a.当p＞2时，∀β∈Δ，〈β，β〉＝2，有（f（β）｜f（β））＝〈β，β〉（modp）＝2，因此f（Δ）⊂Γ.下证f是单射，假设β，β′∈Δ，f（β）＝f（β′），要证β＝β′.

对∀γ∈Δ，（f（β）｜f（γ））＝（f（β′）｜f（γ）），由引理1得〈β，γ〉＝〈β′，γ〉（modp），因此O（β）＝O（β′），这意味着β和β′属于Δ的同一个不可约子根系.分两种情况讨论：

（a）若该子根系为型A2的，对∀γ∈Δ（A2），由〈β，γ〉＝〈β′，γ〉（modp），恒有β＝β′.

（b）若该子根系不为型A2的，由O（β）＝O（β′）推出β＝±β′.若β＝－β′，则对∀γ∈Δ，〈－β′，γ〉＝〈β′，γ〉（modp），由性质3，〈β′，γ〉＝｛－1，0，1，±2｝，矛盾，所以β＝β′.

b.当p＝2时，∀β∈Δ＋，〈β，β〉＝2，所以f（Δ＋）⊂Γ∪｛0｝.因此只需证f（Δ＋）∪｛0｝→Γ∪｛0｝是单射.设β，β′∈Δ＋∪｛0｝，f（β）＝f（β′），下证β＝β′.

同p＞2的情形，对所有的γ∈Δ，〈β，γ〉＝〈β′，γ〉（mod2）.由此O（β）＝O（β′）.

（a）当O（β）＝O（β′）＝Δ时，由引理2，β和β′要么为子根系A1的单根，要么为｛0｝.由于f限制到｛0，α1，α2，…，αn｝是单射，所以β＝β′.

（b）当O（β）＝O（β′）≠Δ时，由引理2，β和β′同属于Δ＼O（β）所在的不可约子根系中.因此不妨假设Δ是不可约根系.

由引理3若Δ是型A2，Ak（k≥4），E6，E7，E8的，显然β＝β′.若Δ是型Dk（k≥3）的，β和β′都属于子根系A1（不一定是同一个）中.若β和β′属于同一个A1，则有β＝β′.若它们不属于同一个子根系A1中，Δ（Dk）的根是 ｛ εi±εj，i≠j｝ ⊂ℝk.令β＝εi±εj，由O（β）＝O（β′），则β′＝εi∓εj.因为f（2εj）＝f（β）－f（β′）＝0，所以对∀l，f（2εl）＝2f（εl－εj）＋f（2εj）＝0

由此，对所有的m≠l，f（εm＋εl）＝f（εmεl）.特别对单根αk－1＝εk－1－εk，αk＝εk－1＋εk，f（εk－1－εk）＝f（εk－1＋εk），这与f限制到单根是单射，矛盾.故β和β′属于同一个A1，有β＝β′.

2 型E7根系的结构

2.1 型E7根系的分层

在向量空间ℝ8中，E8根系为

基为Π＝｛αi：1≤i≤8｝ ， 具体为

型E7的根系为型E8的根系的子根系，其Dyn图［4］如图1所示.

图1 型E7根系的Dyn图Fig.1 Dynkin diagrams about root system of type E7

下面对型E7的根系进行分层.约定E7的单根的顺序对应根系的包含关系为

记

E7的正根满足为了方便下一步的讨论，将放在同一层仍记作

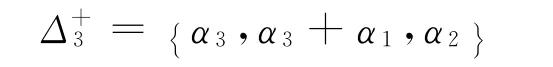
由此，E7对应的分层其中于是En（3≤n≤7）的根系记则Δs和Δs′总是表示连续的层.E7的正根［5］分层为

定理2 ∀β∈Δ＋s，β表示成α1，α2，…，αn的线性组合时系数ks＝1.

对每一层，Hs表示图：其顶点为Δ＋s中的根；若β，β′∈Δ＋s，±（β－β′）为单根，则β和β′之间用一条边连接.这样的Hs为Δ＋s上的偏序图，称为哈斯图，如图2所示.哈斯图很好地刻画了Δ＋s上的偏序关系，但正交性并没有从中体现.

图2 每一层的哈斯图Fig.2 Hasse diagrams about every stratum

2.2 映射

Δ为E7的根系，p＝2.设F＝（ℤ／2×ℤ／2，⊕）表示非循环的四元群，分别用0，1，2，3代表（0，0）（0，1）（1，0）（1，1），由此这个群的元素为｛0，1，2，3｝，定义F上的“⊕”运算，见表1.

表1 F上的‘⊕’运算Tab.1 Operation‘⊕’on F

这样F是一个ℤ／2上的二维向量空间，在其上定义一个双线性型

取V＝F3，将（a，b，c）∈V简记为abc，定义V上的“⊕”

在V上定义双线性型

定理3 f：Δ＋→V∪｛0｝是双射.

证明 由定理1知f是单射，又因为＃（Δ＋∪0）＝＃（V）＝64，因此f为双射.

设Γs表示层Δ＋s在f下的像，通过计算得到

定理4 层Γ7＝｛abc∈V｜a，b，c有且仅有一个为0｝.

证明 由Γ7的列举，显然.

2.3 偏序和正交结构

对abc，a′b′c′∈V，若｛a＝a′，b＝b′，c＝c′｝有且仅有一个成立，则记abc～a′b′c′.

定义图O（V）：以V中元为顶点，对abc，a′b′c′∈V且abc≠a′b′c′，若（abc｜a′b′c′）＝0，abc，a′b′c′有一条边连接.

图T（V）：以V中元为顶点，若abc～a′b′c′，则abc与a′b′c′有一条边连接.

若X⊂V，O（X）和T（X）各自表示O（V）和T（V）被限制到X上的子图.

注 由推论1，可知图O（X）中若两顶点之间有边连接，则这两个顶点对应的根正交.图O（X）可以反映根系的正交结构.又图O（X）有边连接的两个顶点满足（abc｜a′b′c′）＝0，而图T（X）有边连接的两个顶点满足｛a＝a′，b＝b′，c＝c′｝有且仅有一个成立，前者的条件需要计算可以得出，后者则仅需观察元素的特征就可以得出，因此图T（X）更有利于实现直观化，但是前提是图T（X）与图O（X）是一致的.

定理5 a.图T（Γ7）和O（Γ7）是一致的；b.图T（Γ／Γ7）和O（Γ／Γ7）是一致的.

证明 因为（abc｜a′b′c′）＝（a｜a′）＋（b｜b′）＋（c｜c′），所以（abc｜a′b′c′）＝0⇔ ｛（a｜a′ ），（b｜ b ′），（c｜ c ′）｝中有奇数个为0.

a.设abc和a′b′c′是Γ7中的不同的元素，由定理4，｛a ，b ，c｝和｛a′ ，b′，c′｝中仅有一个为零.若a＝a′＝0，那么（abc｜a′b′c′）＝0⇔b≠b′且c≠c′⇔abc～a′b′c′.若a＝b′＝0，那么（abc｜a′b′c′）＝0⇔c＝c′⇔abc～a′b′c′.由对称性，其余情况可类似推出.

b.设abc和a′b′c′是Γ＼Γ7中的不同元素，由定理4，｛a ，b ，c｝和｛a′ ，b′，c′｝中零的个数为0或2.以下分情况讨论：

（a）a，b，c，a′，b′，c′全部非零，那么

（abc｜a′b′c′）＝0⇔｛a≠a′，b≠b′，c≠c′｝中有偶数个成立⇔abc～a′b′c′；

（b）a，b，c，a′非零且b′，c′＝0，那么（abc｜a′b′c′）＝0⇔a＝a′⇔abc～a′b′c′；

（c）a，a′非零且b＝c＝b′＝c′＝0，那么（abc｜a′b′c′）≠0，abc～a′b′c′；

（d）a，b′非零且b＝c＝a′＝c′＝0，那么（abc｜a′b′c′）＝0，abc～a′b′c′.

（e）其它情况，由对称性得证.

推论2 对β，β′∈Δ7或β，β′∈Δ（E6）且β≠β′，〈β，β′〉＝0当且仅当图T（V）中f（β），f（β′）有一条边连接.

证明 因为〈β，β′〉＝0⇔（f（β）｜f（β′））＝0⇔f（β）～f（β′）.

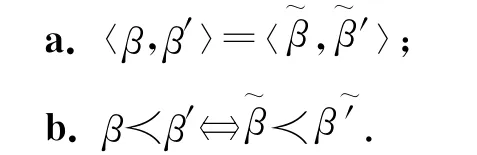
引理5 设x1，x2∈Γ7.a.若x1与x2正交，则存在唯一向量x3∈Γ，使｛x1，x2，x3｝是两两正交的，且x1⊕x2⊕x3＝0；b.若x1⊕x2∈Γ7，则x1与x2正交.

证明 设β1＝f－1（x1）∈Δ＋7，β2＝f－1（x2）∈Δ＋7，将β1和β2看作根系E8的根.

a.若x1，x2正交，则〈β1，β2〉＝0.又对任意β∈Δ＋7，〈α8，β〉＝－1，α8＋β∈Δ（E8）.所以α8＋β1∈Δ（E8）.又〈α8＋β1，β2〉＝－1，所以α8＋β1＋ β2∈Δ（E8）.

再证唯一性.设x3是与x1和x2正交的任意向量，β3＝f－1（x3）∈Δ＋7，有〈α8＋β1＋β2，α8＋β3〉＝－1，所以γ＝－（2α8＋β1＋β2＋β3）∈Δ（E8）.γ的表达式中系数k8＝－2，而Δ（E8）中仅有仿射根具有这个性质.因此从而

b.若x1和x2不是正交的，那么β1－β2是一个根，但其不在Δ7中，因此x1⊕x2∉Γ7.

定理7 设x，y∈Γs，（x｜y）＝0⇔x⊕y∈Γ7.

证明 由引理4中c，x⊕zs，y⊕zs∈Γ7.因此

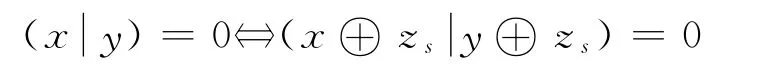
由引理5，x⊕y＝（x⊕zs）⊕（y⊕zs）∈Γ7.

注 此定理给出了同一层两个根的正交性的判定方法.

下面在一个立方体上将Γ7具像化，由定理6，其它层上的根的正交和偏序关系也可类似得到.Γ7的元素被排列如图3（a）.

在图3（a）中，由定理5及图T（V）的定义，对∀x∈Γ7，Γ7中与x正交的元素y被描述为：

a.若y与x在立方体的同一个面上，那么y与x不在同一行或同一列；

b.若y与x在不同的面上，那么y位于x所在行或列延伸的行或列.图3给出了Γ7中与021正交的根的像的集合为：｛012，013，032，033，101，120，201，220，301，320｝.

图3 第7层上的正交和偏序关系Fig.3 Orthogonality and partial order on the seventh stratum

对x，y∈Γ7，若y＝x⊕ai，其中ai＝f（αi），i＝1，2，…，6，则x和y之间用一条边连接.这样在立方体中复原Δ＋7的偏序关系图H7（图3（b）），图中i，i＝1，2，…，6表示该边连接的x和y满足y＝x⊕ai.

［1］ Purbhoo K.Compression of root systems and the E－sequence［J］.The Electronic Journal of Combinatorics，2008，15（1）：26－46.

［2］ Wildberger N J.A combinatorial construction for simply－laced Lie algebras［J］.Adv Appli Math，2003，30（5）：385－396.

［3］ Humphreys J E.Introduction to Lie algebras and representation theory［M］.New York：springer－Verlag，1972.

［4］ 苏育才，卢才辉，崔一敏.有限维半单李代数简明教程［M］.北京：科学出版社，2008.

［5］ 田丽，胡建华.有限域上型Dn，E6，E7，E8，F4的Chevalley群之间的同态［D］.上海：上海理工大学，2011.

［6］ Purbhoo K，Sottile F.The recursive nature of cominuscule Schubert calculus［J］.Adv Math，2008，217（5）：1962－2004.

［7］ Godsil C，Royle G.Algebraic graph theory［M］.New York：Springer－Verlag，2001.

［8］ Wildberger N J.Minusculeposets from neighbourly graph sequences［J］.European J Cominatorics，2003，24（6）：741－757.

［9］ Belkale P，Kumar S.Eigenvalue problem and a new product in cohomology of flag varieties［J］.Invent Math，2006，166（1）：185－228.

［10］ Stembridge J R.On minuscule representations，plane partitions and involutions in complex Lie groups［J］.Duke Math J，1994，73（2）：469－490.