虞志坚

（台州学院 数学与信息工程学院，浙江 临海 317000）

关于测度的教学探究

虞志坚

（台州学院 数学与信息工程学院，浙江 临海 317000）

本文对《实变函数》中的重要概念测度的教学作了若干探究。既要从直观上介绍Lebesgue测度的原始定义，也要使学生明白Lebesgue的原始定义依赖于原集合的性质而不能进行推广的缺陷。在此基础上更要强调Caratheodory的定义脱离了原集合的具体性质便于进一步抽象推广。

实变函数；Lebesgue测度；测度；抽象测度；教学探究

对于地方本科院校的数学系学生来说，《实变函数》是一门难度较大的课程。测度是《实变函数》的一个核心概念，所以，能否深刻理解并掌握测度这个核心概念，是学生学好《实变函数》这门课程的关键。因此，为使学生能学好《实变函数》，作为任课教师应当对测度的教学进行探索研究，以帮助学生尽快掌握测度的本质，并为下一步继续学习《实变函数》打下扎实的基础。笔者在多轮《实变函数》教学实践的基础上，对测度的教学进行了梳理探究。

1 关于测度的引入

测度概念的引入通常有两个途径。一种是从具体到抽象，即从具体的R1或R2空间开始，定义Lebesgue测度，然后将它推广到抽象空间上，得到抽象的测度［1，2］；另一种是从抽象到具体，具体做法是直接在一般的抽象空间上，以测度必须具备的最核心的性质作为公理直接定义测度［3］，再将R1或R2空间上的测度作为具体的例子。两者各有优点，后者对于基础好的学生，特别是国内一流重点大学的学生来说，能够以最短的时间直接深入测度理论的核心，这是它的优点。但对于基础相对薄弱的学生来说，这种方法显得突兀，不大容易接受。前者对于初学者特别是对地方本科院校的学生来说更容易理解接受。所以，对于一般地方性本科院校的学生，我们认为采用第一种方法为好。

2 关于一维点集与n维点集的测度

常见的《实变函数》教材大致可以分为两类，一类介绍一维点集的测度与积分［1］，另一类介绍n维点集的测度以及相应的积分［2］。两者各有所重，也各有优点。前者直观明了，对于熟悉定积分内容的学生，可以直接过渡到测度理论和Lebesgue积分理论；但是，我们不该将目光只停留在一维，而且一维点集的测度与积分跟n维点集的测度与积分在内容上并无本质区别，在叙述上也可以统一处理。因而，我们认为，可以直接从n维点集入手介绍测度与积分理论，并将一维的情形作为其特殊例子来处理，应当是比较恰当的处理方法。

3 关于Lebesgue测度的教学

对于从具体到抽象这一引入勒贝格测度的途径，也有两种选择。一种是测度论的奠基人Lebesgue的原始做法，即先定义点集E的外测度m*（E）与内测度m*（E），当它们相等的时候定义点集E可测［1］；另一种是先定义点集E的外测度m*（E），然后通过Caratheodory条件定义测度，这是希腊数学家Caratheodory的做法［2］。下面分别介绍之。

定义1［2］56设E是Rn中的点集，E的外测度m*（E）定义为：

其中 Ii｛｝是覆盖E的开区间列。

定义2［2］62设E是Rn中的有界点集，I是包含E的任一开区间，定义E的内测度m*（E）为：

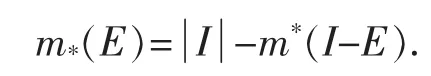
若m*（E）=m*（E），则称E是Lebesgue可测的，此时m*（E）=m*（E）就称为点集E的Lebesgue测度，记作m（E）。设E是Rn中的无界点集，若对于任何开区间I，有界集E∩I都是Lebesgue可测的，则称是Lebesgue可测的。

无疑，Lebesgue的做法直观上是最容易被接受的，因为这跟数学分析中的方法是一脉相承的。但是，这一方法并不是最简洁的，定义中有界集和无界集受到不同的对待，并且同时出现了内外两种测度，使用起来很不方便。更重要的是，这个测度的定义由于依赖原集合的性质，因而不能进行推广。这是这个定义的缺陷，它妨碍了测度理论的深入学习。

定义3［2］62设E是Rn中的点集，如果对于任一点集T，都有

则称E是Lebesgue可测的。这时E的外测度m*（E）就称为E的Lebesgue测度，记作m（E）。

定义3中的（#）式称为Caratheodory条件，T称为试验集。这个定义是说，将E作为尺子，把T分为互不相交的两部分去度量，如果对于任何试验集T，Caratheodory条件都成立，那么E就是可测的。可以证明上面这两种测度的定义是等价的。Caratheodory条件反映了测度的内在联系，使得这个定义脱离了点集E的具体性质，从而可以进行抽象的推广。因此，初看起来Caratheodory条件并不那么自然直观，但这却是引入可测集的最简捷的方法。Caratheodory条件反映了Caratheodory对Lebesgue测度的深刻理解。

在教学中，对于地方性本科院校的数学系学生，如台州学院学生，既要从直观上介绍Lebesgue测度的原始定义，也要使他们明白Lebesgue的原始定义依赖于原集合的性质而不能进行推广的缺陷。在此基础上更要强调Caratheodory的定义脱离了原集合的具体性质便于进一步的推广深入，这是大多数《实变函数》教材采用Caratheodory定义的原因。

4 关于测度概念的进一步提升

从上面定义中可以看到，Rn中的任何点集都有外测度。我们知道，外测度只有次可加性而没有可列可加性，而测度是要满足可列可加性的，所以，我们要找到Rn的子集族，使得外测度在此子集族上成立可列可加性。

Rn的子集族X称为一个σ-代数，如果它满足：

（1）Rn，Ф，I∈X，其中I为任何区间，

（2）若A∈X，则AC∈X，

设Ω为一非空集，2Ω是Ω的幂集，即Ω所有子集构成的集族。但Ω的子集太多，我们得剔除掉那些性质“不好”的集合。设映射］，满足：

（1）m*（Ф）=0，

称E∈2Ω是m*-可测的，如果对任何的T∈2Ω，成立

容易证明，全体m*-可测集构成一个σ-代数，记为M*。可以证明，对任何，如果它们两两不交，则，即可列可加性成立，这时上面的映射］（它先是外测度）就成为M*上的测度。

到这里，我们已经看到，外测度是定义在幂集2Ω上的非负函数，而测度是定义在幂集2Ω中由m*-可测集构成σ-代数M*上的非负函数。即，通过Caratheodory条件，缩小外测度的定义域，便得到了测度。

最后，我们指出，抽象的测度理论可以完全建立在公理化的基础上，从中我们可以几乎看不到任何构造性的痕迹。由此可见，从Lebesgue的原始方法到Caratheodory的方法，是测度从具体到抽象的飞跃——测度理论从此在众多领域都起到了很大的作用。例如，当将测度］的值域限制为［0，1 ］时，测度便是我们知道的概率。换言之，概率是特殊的测度。

在教学中，在深入讲授了具体的测度以后，可以恰当介绍抽象测度的内容，以便提升学有余力学生的学习水平。

［1］郑维行，王声望.实变函数与泛函分析概要（第一册）［M］.2版.北京：高等教育出版社，1986.

［2］程其襄，张奠亩，魏国强，等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2010.

［3］胡适耕.实变函数论［M］.北京：高等教育出版社，1999.

Teaching Explorations on Measure

YU Zhi-jian

（School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China）

In this paper, some teaching explorations on important concept measure in function of real variable are done.It is necessary not only the original definition of measure should be introduced,but also the fault of this definition depending on the specific properties of point sets should be pointed out.Furthermore,it is crucial to be emphasized that the definition of measure based on the Caratheodory condition is convenient to be generalized since this definition separates itself from the concrete characters of point sets.

function of real variable;Lebesgue measures;measures;abstract measures;teaching explorations

10.13853/j.cnki.issn.1672-3708.2014.06.016

（责任编辑：耿继祥）

2014-11-05；

2014-11-27

虞志坚（1971- ），男，浙江台州人，副教授。