王丽英，张友安，赵国荣

（海军航空工程学院1.系统科学与数学研究所；2.控制工程系，山东 烟台264001）

近年来，伪谱法（p法）和网格细化法（h法）在求解非线性最优控制问题的数值解上得到了广泛的应用[1－3]。文献[1]提出了一种p法网格细化策略，缺点是要提前获知不连续点和奇点个数及位置。文献[2－3]分别提出了一种基于多分辨率的自适应h法轨迹优化算法和基于密度函数的网格点分布算法，优点是可以较好地捕捉状态变量、控制变量的不连续性和高阶非平滑性；缺点是计算效率低。起源于有限元法的自适应hp法，结合了p法和h法的优点，在流体力学和偏微分方程的求解中得到广泛应用[4－7]。为同时提高伪谱法求解非线性最优控制问题的精度和计算效率，文献[8]将hp思想引入最优控制问题的求解中，提出了hp自适应伪谱法，在实施过程中忽略了轨迹的平滑性；文献[9－10]则给出了一种变阶自适应伪谱法，以轨迹的曲率作为改进精度方式的标准，相比文献[8]，该算法考虑了轨迹的平滑性，但在执行h法细化时，是根据轨迹曲率密度函数定义新增网格点的个数和位置，对于无约束或约束较少的情况，该算法很实用，但对于多约束条件下的复杂优化问题来说，却要耗费大量的优化时间。

本文在文献[8－9]的基础上，基于Radau伪谱法给出了一种改进的hp自适应网格细化算法。以高超再入飞行器轨迹优化为例，将该算法和全局伪谱法及局部伪谱法在解的精度、优化计算时间、迭代次数等方面进行了比较，结果表明hp自适应网格细化算法能以较少的计算代价得到较高精度的解。

1 多区间轨迹优化问题阐述

多约束条件下的轨迹优化问题可描述为下列非线性最优控制问题：定义状态－控制变量，使Bolza型代价函数最小化：

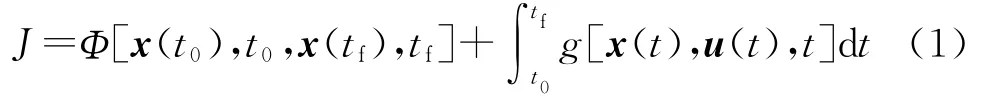
满足约束条件：

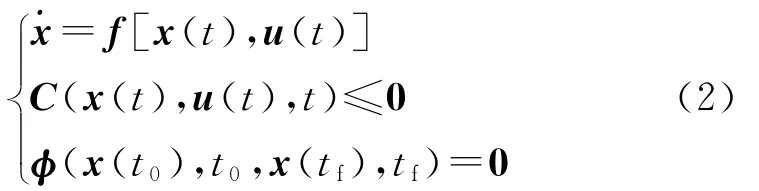
多区间非线性最优控制问题是指将问题（1）、问题（2）的时间区间[t0，tf]划分为K个子区间，用t0＜t1＜…＜tK＝tf表示K＋1个网点，Nk（k＝1，…，K－1）表示第k个子区间[tk－1，tk]内的配点数（这里，定义网点为相邻区间的连接点；配点为单个区间内的节点；整个区间的节点数等于网点数与配点数之和）。进行下述时域变换：

将时间t∈[tk－1，tk]转变成τ∈[－1，＋1]。

对于转换后的多区间最优控制问题，采用hp－LGR伪谱法作为基本的离散化方法，将其转化为非线性规划问题，具体步骤参见文献[10]。

2 改进的hp自适应网格细化算法

2.1 误差评估准则

在数值求解过程中，一般不能得到原连续时间最优控制问题的确切解，但若给出的数值求解方法能够精确地近似原问题，则微分－代数约束方程应该在任意点上被满足。因此，以微分－代数约束方程在配点间的满足程度作为解的近似误差评估准则。

取相邻配点间等间距分布的3个点作为误差评估准则的采样点，即

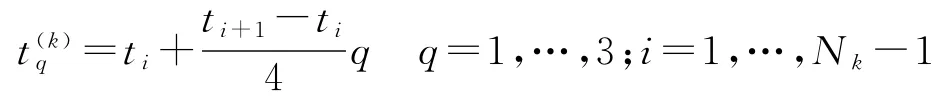
为叙述方便，将[tk－1，tk]内的采样点定义为，于是微分－代数约束方程在采样点上的残差表示为

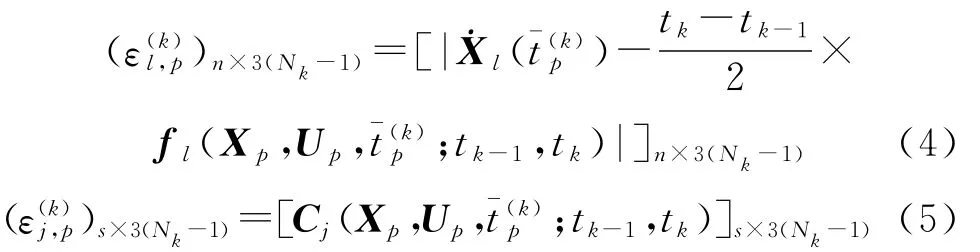
式中：l＝1，…，n，表示状态变量的个数；j＝1，…，s，表示路径约束的个数；p＝1，…，3（Nk－1），表示采样点表示第l个状态在第p个采样点处的残差绝对值表示第j个路径约束在第p个采样点处的残差。式（4）表示动态约束残差矩阵；式（5）表示路径约束残差矩阵。对于路径约束来说，当式（5）中的元素全为负值时，表示满足设定的要求；当存在大于零的元素时，则表示不能满足设定的要求。

设ε为给定的误差门限值。于是，当式（4）中的所有元素都小于设定的ε且式（5）中的元素全为负值时，认为达到求解精度要求；反之则需要进一步提高求解精度。下面以第k个子区间[tk－1，tk]为例，具体介绍改进求解精度要求的措施。

2.2 提高求解精度的策略

2.2.1 路径约束残差起主要作用

2.2.2 动态约束残差起主要作用

令（xl，p）n×3（Nk－1）表示n个状态变量在p个采样点上的离散值所构成的状态矩阵，为矩阵（xl，p）n×3（Nk－1）中相应 于最大 残差的状态所在的行向量，即，则第l个状态在第p个采样点处的曲率为

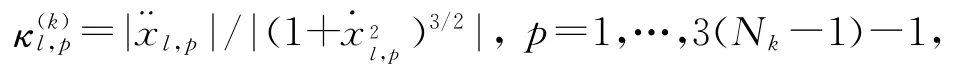
设表示曲率的算术平均值，即

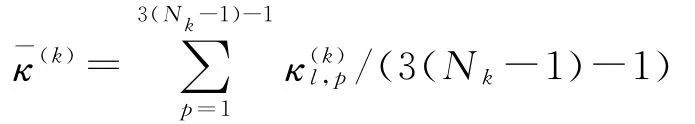
令

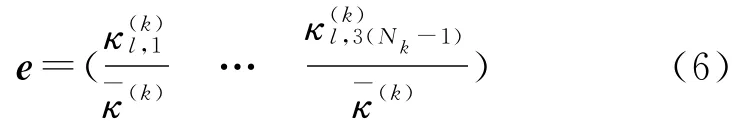
若式（6）中的每个元素都比ρ小（ρ为一设定值），则认为该区间内的曲率具有一致形式，此时，通过增加区间内插值多项式的维数来提高求解精度。设表示区间[tk－1，tk]在第i次迭代时的配点数，表示第i＋1次迭代时的配点总数，N（＋）表示新增加的配点数，则

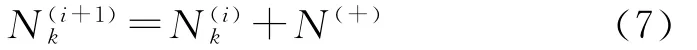
若式（6）中存在比ρ大的元素，则认为该区间内存在一个（或多个）较大的曲率，即轨迹相对来说是非平滑的，此时，需要将该区间作进一步的细化以提高求解精度。

①确定新网点的位置。

取式（6）中元素的局部最大值对应的采样点作为新增加的网点。

②确定新增加区间内配点的个数。

与2.2.1节相同，在每个新增加的区间内设定N（0）个配点。

2.3 算法具体步骤

具体算法步骤总结如下。

①初始化。给定误差门限值ε和初始状态x0；选取K个子区间，每个区间内设定N（0）个配点。

②在给定的状态估计值和节点分布下求解NLP，若所有区间的＜ε，则停止迭代，若存在某个ε，则继续③；

④在路径约束的残差最大处进行网格细化，令N（0）为新增区间内的配点数，转⑥；

⑤若式（6）具有一致形式，则增加该区间内的配点数，如式（7）所示；若式（6）具有非一致形式，则进行网格细化，取式（6）中元素的局部最大值对应的采样点作为新增的网点位置，在每个新增加的区间内设定N（0）个配点；

⑥在所有的网格区间都被更新后，返回②。

3 应用实例

下面以再入飞行器轨迹优化问题为例，对本文算法进行验证。

3.1 再入轨迹优化问题

再入轨迹优化的数学模型，即详细的3－D运动方程参见文献[11]。同时将升力参数CL和阻力参数CD表示为攻角α和马赫数的函数[11]：

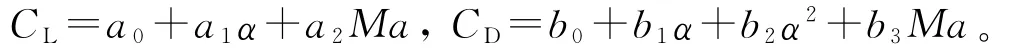
为限制执行机构的变化速率，令＝u1，＝u2，于是将3－D运动方程改写为向量形式的8状态运动方程，其状态空间X1和控制空间U1定义如下：

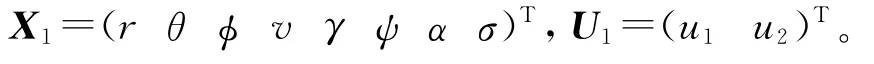
式中：r0为飞行器距地心的距离；θ，φ分别为经度、纬度；v为飞行速度；γ，ψ，α，σ分别为飞行路径角、航向角、攻角、倾侧角；u1，u2分别为攻角变化率、倾侧角变化率。

以再入航程最大为优化目标，即J＝－φ（tf），其中，tf为末端时刻。同时考虑以下的约束条件：

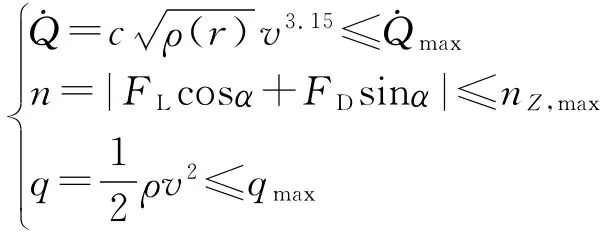
式中：FL为升力，FD为阻力；c＝34 882.985 5，为常数＝2 453kW/m2；nZ，max＝4，qmax＝335.2kPa。

②终端条件约束。

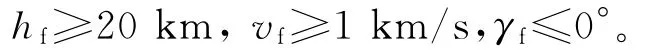
3.2 仿真分析

仿真中状态变量、控制变量的边界限制如下：

仿真中涉及到的各种参数设置见表1。

取N（0）＝2，N（＋）＝5，ρ＝2；N0，Nc分别表示不同算法初始化时选取的区间个数和每个区间内的配点数。为简化表达形式，以下表述中的p代表全局Radau伪谱法；h代表分段Radau伪谱法；hp代表改进的自适应 hp－Radau伪谱法。E，tc，Cpt，MI，IT，OF分别表示优化结束时的最大微分－代数约束的近似误差、优化计算时间、优化结束时的配点个数、网格区间个数、迭代次数和目标函数值。整个求解过程是在普通PC机上进行的，其中，CPU为1.73G/Pentimu Dual，内存为DDR 1.0G，操作系统为Windows XP，编程环境为 Matlab R2009a。

表2给出了3种伪谱方法在不同精度要求下的最大近似误差、优化时间、优化结束时所需的配点总数、子区间个数、迭代次数及代价函数绝对值间的比较结果，从中可得到以下结论：①不同精度标准下，p法在优化过程中得到的微分－代数约束误差均最大；②10－3和10－4的精度要求下，h法和hp法在优化速度、求解精度上相差不大，相对来说hp法的计算精度最高；③随着精度要求的提高（10－5），优化所需的配点总数、子区间的个数、迭代次数均逐渐增多，相应地也导致了优化时间的增长，符合伪谱法求解最优控制问题的特点。同时可以看出，hp法在求解精度和优化时间上最具优势。

表1 仿真参数设置

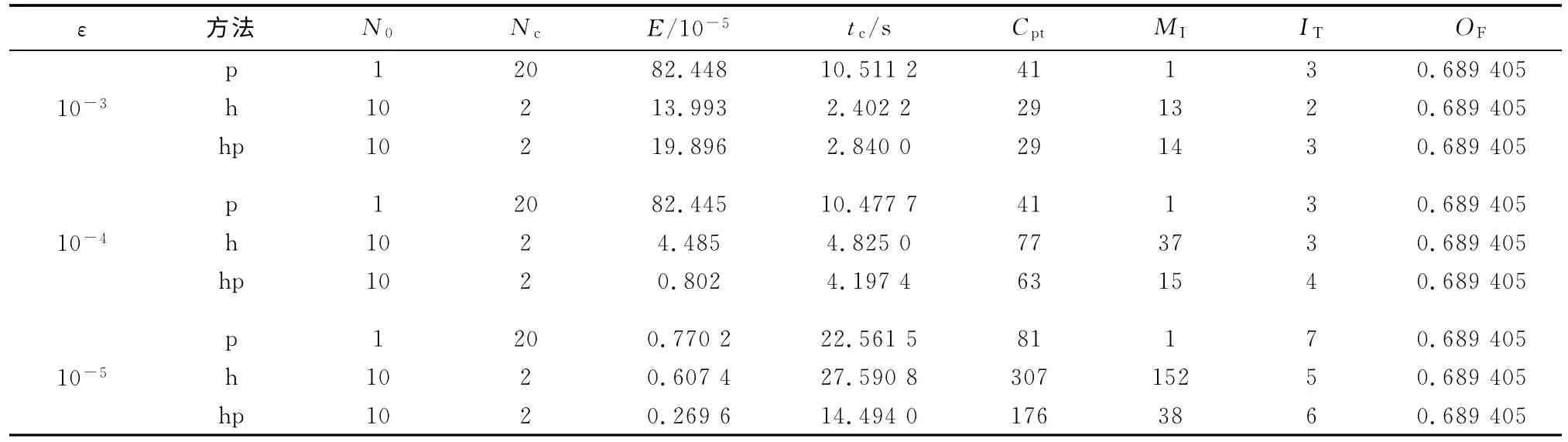
表2 不同伪谱方法的优化结果比较

图1给出了10－4精度下不同伪谱法的节点分布特点（图中纵坐标无实际物理意义，仅为图示方便，将采用不同方法优化得到的节点分别投影于y＝1，y＝2和y＝3所代表的3条直线上），从图中可以看出：①p法采用的是一个区间，通过增加区间内节点个数提高求解精度要求，保持了伪谱法节点两端密、中间疏的分布特点；②h法通过细化子区间的方式提高求解精度要求，所有子区间内的配点数是相同的，可看出每3个点构成一个区间；③hp法的节点分布明显不同于其它2种伪谱方法，不具备统一节点分布标准。

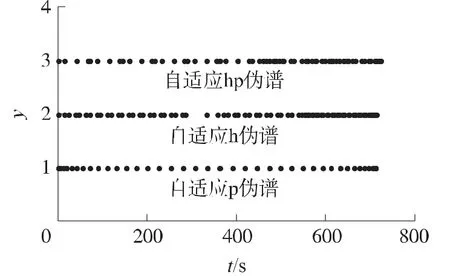
图1 不同伪谱法的节点分布

上述分析过程表明：hp法与其他2种优化方法相比，能够以较少的计算代价得到较高精度的解。

图2、图3分别给出了本文算法与文献[8－9]中的算法在求解3.1节轨迹优化问题中得到的部分状态轨迹和路径约束变化曲线；3种hp算法优化求解过程所需的优化时间、节点总数及迭代次数间的比较结果如表3所示。

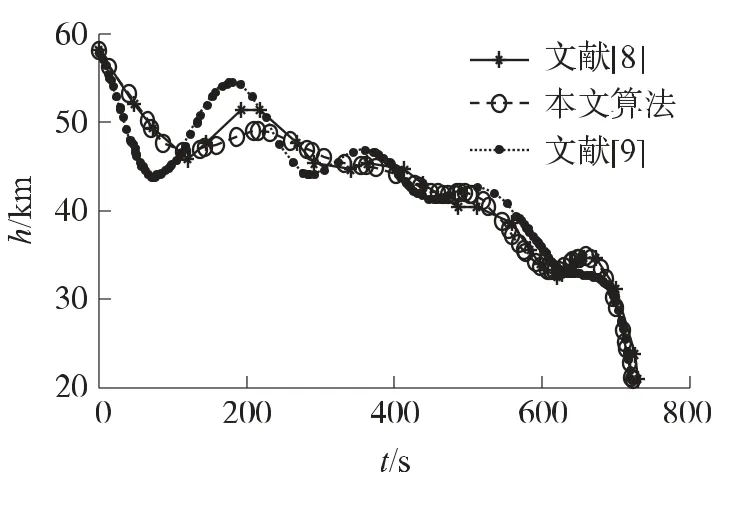
图2 高度变化曲线

取误差门限值ε＝10－4，由图可以看出，从最优轨迹的平滑性上考虑，文献[9]的算法最好，其次是本文算法，文献[8]最差；而由表3则可看出，文献[9]所需的优化时间最长。由于研究目的是实现再入轨迹的快速优化，因此，综合衡量轨迹精度和优化时间，本文所给算法结合了文献[8]和文献[9]的优点，更适合快速求解高超飞行器的再入轨迹优化问题。

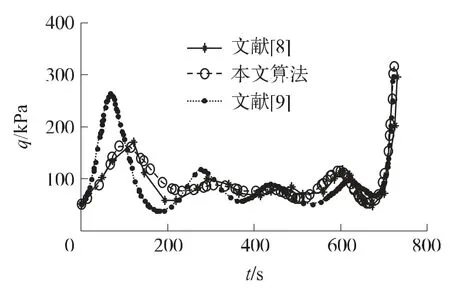
图3 动压变化曲线

图4和图5分别为优化得到的最优控制信号及其随时间的变化速率曲线。结合两图可以看出：①优化过程中控制变量的大小及变化速率均在要求的设定范围内；②攻角大部分时间保持在15°～20°之间，即保持大攻角飞行，最大程度地减少热载的作用，符合高超热防护的需求。优化得到的三维最优轨迹如图6所示。

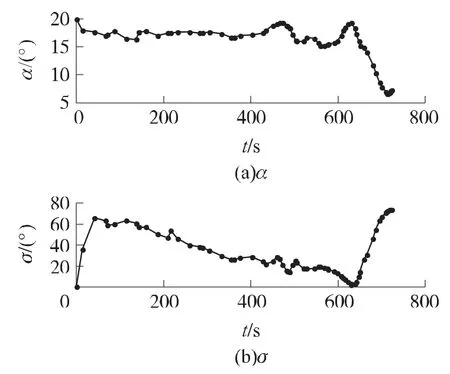
图4 控制信号

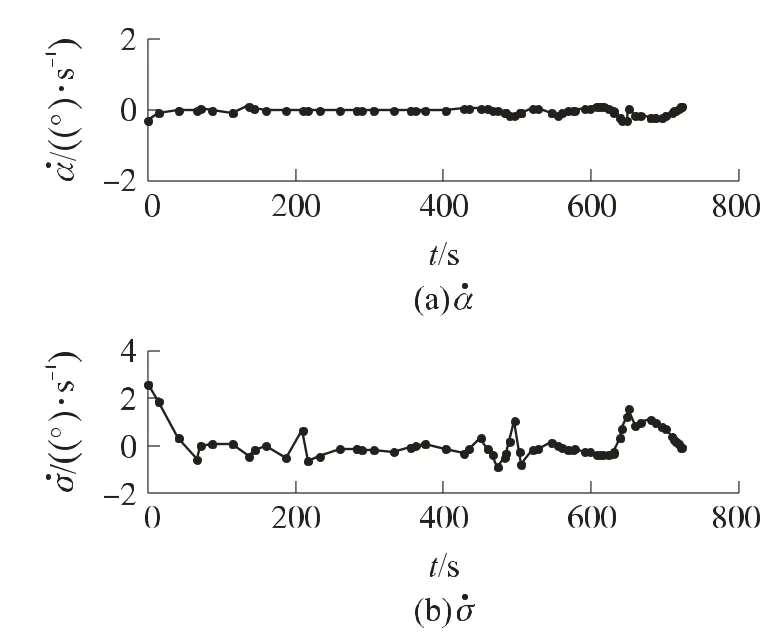
图5 控制信号变化率

图6 三维最优轨迹

为分析hp－LGR伪谱法计算最优轨迹的精度，将计算得到的最优控制信号带入原微分方程，用Matlab中的ode45命令进行数值积分，状态变量的积分轨迹与最优轨迹间的误差曲线如图7，可以看出两者间的误差较小；表4为末端状态变量实际值与期望值间的比较结果，从中可以看出终端约束均得到满足，期望的落点位置与实际位置间的误差很小，表明了hp－LGR伪谱法具有较高的求解精度。

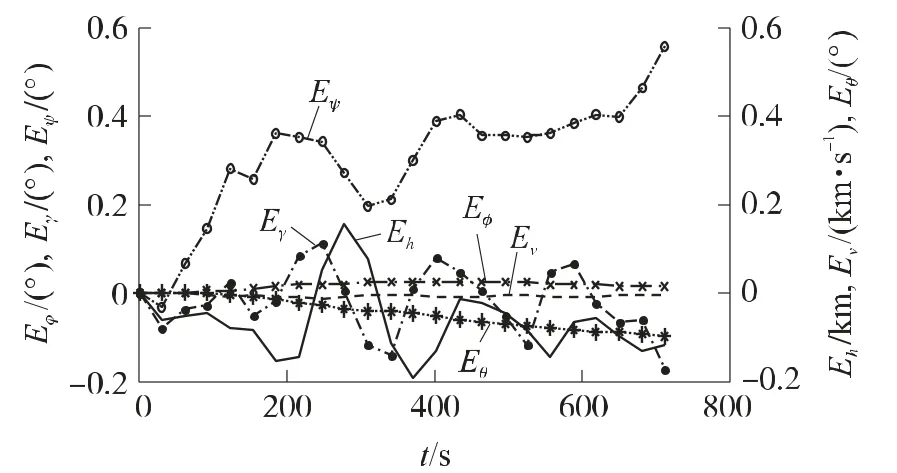
图7 误差曲线

表4 末端状态误差

图8为路径约束随时间变化曲线，从图中可以看出：热流密度、动压和过载约束均在设定的范围内；且热流密度的峰值出现在再入初期，随着高度的降低、大气密度的增大，热流密度逐渐减小，动压和过载则逐渐变大，符合高超再入轨迹的特点。

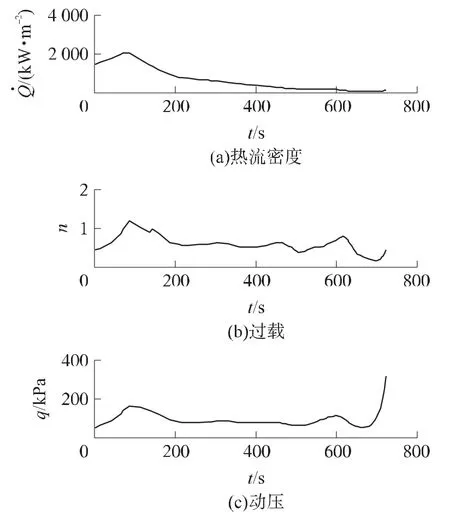
图8 路径约束随时间变化曲线

4 结论

基于hp－LGR伪谱法给出了一种求解非线性最优控制问题的hp自适应网格细化算法，通过增加插值多项式维数或细化网格的方式提高解的精度，优化结束时的微分－代数约束最大误差为0.0802×10－4，满足设定的精度要求，优化时间为4.197 4s。仿真结果表明：

①与全局伪谱法和局部伪谱法相比，hp伪谱法充分结合了p法的快速收敛性和h法的计算稀疏性，能够以较少的计算代价得到较高精度的解；

②与已有hp算法相比，本文方法更适合求解多约束条件下轨迹优化问题，具有实时应用的潜力，可作为实时制导的基础。

[1]ROSS I M，FAHROO F.Pseudospectral knotting methods for solving optimal control problems[J].Journal of Guidance，Control，and Dynamics，2004，27（3）：397－405.

[2]JAIN D，TSIOTRAS P.Trajectory optimization using multiresolution techniques[J].Journal of Guidance，Control，and Dynamics，2008，31（5）：1 424－1 436.

[3]ZHAO Y P，TSIOTRAS A.Density－function based mesh refinement algorithm for solving optimal control problems[C]//Infotech and Aerospace Conference.Seattle，Washington：AIAA，2009.

[4]GUI W，BABUSKA I.The h，p，and hp versions of the finite element method in 1dimension.Part I：the error analysis of the p version[J].Numerische Mathematik，1986，49：577－612.

[5]GUI W，BABUSKA I.The h，p，and hp versions of the finite element method in 1dimension.Part II：the error analysis of the h and h－p versions[J].Numerische Mathematik，1986，49：613－657.

[6]GUI W，BABUSKA I.The h，p，and hp versions of the finite element method in 1dimension.Part III：the adaptive h－p version[J].Numerische Mathematik，1986，49：659－683.

[7]GALVAO A，GERRITSMA M，MAERSCHALK B D.Hp－adaptive least－squares spectral element method for hyperbolic partial differential equations[J].Journal of Computational and Applied Mathematics，2008，215（2）：409－418.

[8]DARBY C L，HAGER W W，ANIL V R.An hp－adaptive pseudospectral method for solving optimal control problems[J].Optimal control applications and methods，2011，32（4）：476－502.

[9]DARBY C L，HAGER W W，ANIL V R.A preliminary analysis of a variable－order approach to solving optiaml control problems using pseudospectral methods[C]//AIAA/AAS Astrodynamics Specialist Conference.Toronto， Canada：AIAA，2010.

[10]DARBY C L，HAGER W W，ANIL V R.Direct trajectory optimization using a variable low－order adaptive pseudospectral method[J].Journal of Spacecraft and Rockets，2011，48（3）：433－445.

[11]BETTS J T.Practical methods for optimal control and estimation using nonlinear programming[M].Washington：Society for Industrial and Applied Mathematics，2010.