GaoXiguang（高希光），Song Yingdong（宋迎东）

（1.College of Energy and Power Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China）

INTRODUCTION

Multi-scale mechanics method that evaluates the effective mechanical properties of heterogeneous material is becoming an important method in nowadays engineering.Since the original work was achieved by Bensoussan，Lions and Papanicolaou［1］，the asymptotic homogenization method has been developed for many applications such as topological optimization of composite material［2－4］，multi-scale computational modeling of material degradation［5－6］，etc.To date，most multiscale models in the above areas have been carried out within the context of the finite element method（FEM）［7－12］.The main problem of FEM based approach is the necessity of discretization through out the representative volume element （RVE）.This can result in a complicated modeling process when the microstructure of material is not regular，especially in the case of random defects distribution within porous material.In order to model such composites explicitly，a large number of elements are required，which costs a large amount of computational time and computer memory allocation［13］.

The boundary element method （BEM），an important method，quite different from FEM，provides a novel approach for engineer to ease the analysis in some cases［14－16］.The main advantage of BEM，the reduction of the dimensionality of a problem，becomes very attractive in the case of large scale problems that are as computationally expensive as the large scale modeling［17］.Furthermore，the fast multipole method （FMM）［18］which reduces the number of operations and memory for solving the equation systems has been developed to increase the efficiency of BEM significantly.Therefore BEM is becoming a better way for some people to develop multi-scale model.

Within the framework of asymptotic homogenization theory，BEM based multi-scale models have been developed for predicting the effective elastic properties of linear elastic fiber composites［13，19］.Kazuhiro，et al［20］used wavelet method to reduce the computational cost of BE-based homogenization analysis. Okada，et al used boundary element based homogenization method to obtain the elastic properties of rubber modified epoxy resin and particulate composite materials［21－22］.Song Young Seok，et al used the multi-scale BEM to predict the effective elastic properties for polymer based carbon nanotube composites［23］.Recently，FMM has been introduced into multi-scale BEM and used to estimate the effective elastic properties of the porous material［24－25］.

However，these multi-scale BEM developed within asymptotic homogenization theory are complicated due to the solution process of a set of balance equations in different scales.In order to obtain the solution of the displacement in micro level，an iteration scheme must be used［13］.This reduced the efficiency of this method.In this paper，the formulations of multi-scale BEM are derived without the usage of asymptotic homogenization theory.These formulations are more simple and straightforward than the pioneer ones.As a result，the proposed approach does not need the iteration to obtain the solution of the displacement in micro level.It provides another choice other than asymptotic homogenization multi-scale BEM to estimate the effective properties of periodic linear elastic material.To accomplish the work，the displacement field is decomposed in terms of the linear and fluctuating items.Then，the balance equations are solved by the single-region BEM.The solution provides the formulations of micro-stress field and the effective elastic moduli of the material.Following the derivation of the fundamental equations，two numerical examples for the porous material are presented to prove the accuracy and efficiency of the presented method.

1 BASIC EQUATION

1.1 Theoretical framework of multi-scale method

The homogenization method［26］is employed to construct the collect form of the displacement field representation in the domain of RVE which represents the microstructure of the material（Fig.1）.Let xdenote the position of a point in RVE.Without generality loss，the displacement field within RVE is decomposed in terms of the linear and fluctuating items by

where Aijare linear coefficients andu~idenote the fluctuating displacements.Based on the frequently used concept of homogenization，the homogeneous（effective or global）strainεand stressσ are defined as the average of the local field though out RVE by

whereε andσ are the strain and the stress field at the local level，respectively，Vis the domain of RVE.When some of the heterogeneities are voids or cracks，the deformation of which is not defined pointwisely，the homogeneous strain and stress are redefined as the integration along the outer boundary of RVE by

Fig.1 Illustration of material with periodic microstructure

The accurate estimation of the overall responds of RVE is directly related to the applied type of boundary conditions.Four types of boundary conditions can be used：Uniform tractions，uniform displacement， mixed boundary conditions and periodic boundary conditions［27－30］.Nowadays，the periodic boundary conditions（PBC）are usually preferred since they provide the most reasonable estimations of mechanical properties of heterogeneous materials，even in the cases where the microstructure is not periodic［8，27］.For the two-dimensional case，PBC are presented as

where the superscripts L，R，T，B stand for the left，the right，the top and the bottom parts of RVE boundary，respectively（Fig.2），t is the traction defined through Cauchy′s relations

By combining the Eqs.（1，3－4），we can prove that the linear coefficients Aijappear in Eq.（1）equate to homogeneous strains εij.Therefore，Eq.（1）is reformulated as

Fig.2 Schematic representation of typical RVE under periodic boundary conditions

Eq.（7）connects the homogeneous strain and the displacement filed at different scale.Finally，the theory framework can be presented by a set of equations：

（1）The decomposition of displacement（Eq.（7））.

（2）Periodic boundary conditions（Eqs.（4－5））.

（3）Definition of homogeneous quantities（Eq.（3））.

（4）Equilibrium equations

（5）Displacement-strain relations

（6）Constitute relations at microscopic scale

Therefore，in the theoretical framework presented here，the fluctuating displacement is the fundamental unknown variable.The solutions of these equations give the relations between homogeneous strain and the fluctuating displacement.Then the formulation of the micro-strain and stress are derived by Eqs.（9－10）.By applying the homogeneous Eq.（3），we obtain the global stress and strain.Finally，the relations between these homogenous quantities provide the formulations of effective elastic constants of the material.Based on this approach，several kinds of multi-scale mechanical method can be developed by applying different numerical method.For example，the finite element based method as well as fast Fourier transforms（FFT）based method are developed by Suquet，et al［26］.The high-fidelity generalized method of cell［31］can also be derived by combining this multi-scale approach and the method of weighted residuals.In the following section，we will derive the formulations of a straightforward BEM based multi-scale method by combining the theoretical framework and BEM.

1.2 Fundamental equations of multi-scale BEM

For the two-dimensional problem， the boundary integral equation can be written as

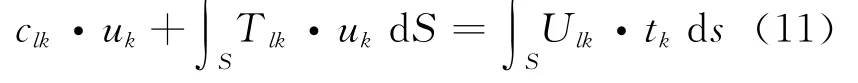
where uj，tjare the displacements and the tractions on the boundary S，respectively，Tij，Uijthe fundamental solutions given in Appendix，and cijis the so-called free term［32］，Sthe boundary of the solid domain within RVE.The symbol∂V mentioned previously is the subset of S.In order to derive the multi-scale boundary integral equation，the displacement in the above equation is substituted by Eq.（3）as

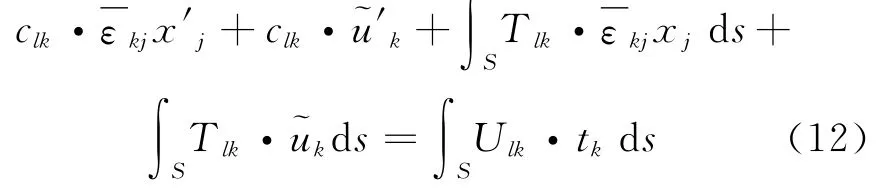
where x′j（j＝1，2）are the location of the source point and~u′kthe fluctuating displacement at the source point.In order to solve the integral equation numerically，the boundary of RVE is discretized into a series of elements.To simplify the formulation，we choose the constant boundary element to discretize the boundary of RVE，therefore，the boundary fluctuating displacements and tractions keep constant. Write the discretized form of Eq.（12）for every element as

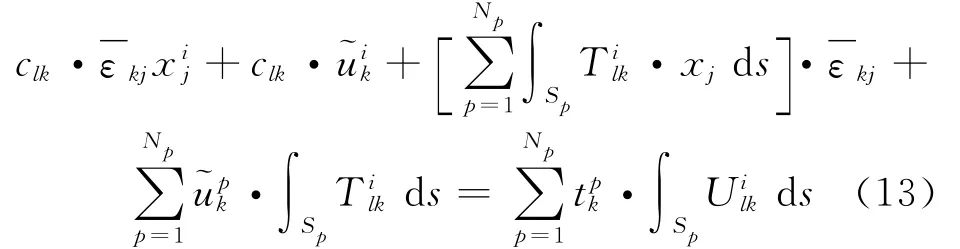
where xijare the coordinates of′i′boundary element′s center，~uikthe fluctuating displacements of′i′boundary element，tpkthe tractions of′p′boundary element，Npis the total number of boundary element，Tilkand Uilkare the fundamental solutions of the source point located at the center of′i′boundary element.After performing the integration，a system of linear algebraic equations is obtained as

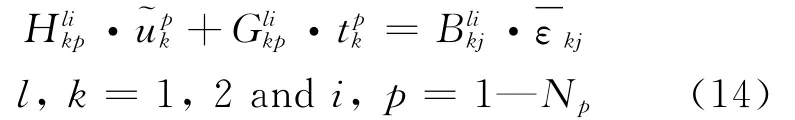
where

The method for calculating Hlikpand Glikpcan be found in many literatures about BEM，while Blikjcan be calculated by numerical integral method like Gauss integral method.The quantities~upkand tpkrepresent all the values of fluctuating displace-ments and tractions before applying PBC.PBC can be introduced by summarizing the corresponding items in Eq.（14），i.e.if~up＋k＝~up－kand tp＋k＝－tp－kwhere the subscriptions p＋and p－denote the corresponding boundary elements in PBC，we present the unknown variables~up－kand tp－kby~up＋kand－tp＋kin Eq.（14）.This results in the substitution of the original coefficients Hlikp＋and Glikp＋by the new coefficients Hlikp＋＋Hlikp－and Glikp＋－Glikp－.Repeating this procedure until all the redundant unknown variables in Eq.（14）are eliminated，then we obtain the final system of equations

where Xdenotes the vector which is composed by~upkand tpk.After solving Eq.（18），all the variables along the boundary are fully determined.

1.3 Homogenized constitutive equations

The homogenized constitutive relations can be expressed as the relations between theσand ε.According to Eqs.（3－7），the formulation of homogeneous stress can be expressed as

Write the discretized form of Eq.（19）for every element as

Eq.（18）implies that the fluctuating displacements of′p′boundary element are the linear functions of homogenous strain as

The substitution of Eq.（21）into Eq.（20）gives the relation betweenσandεas

The simplification of Eq.（22）gives the homogenized constitutive relation

whereEijklare the homogenized elastic constants.Based on Eqs.（22－23），we obtain the formulation ofEijklas

Eq.（24）contains only the geometric and physical parameters of RVE.It can be used to calculate the equivalent elastic constants of material if the microstructure of the material is known.

1.4 Formulations of micro-field

Estimation of micro-stress is important for many applications such as modeling material degradation and fracture.In this section，we will derive the formulation of the micro-stress.In the theoretical framework of BEM，the displacement of any given point x′ within RVE can be expressed as

where xis the point locate at the boundary.The discretized form of Eq.（25）is presented as

Along the boundary element Sp，the tractions keep constant，and the displacement is the summation of the constant fluctuating displacement and the linear item in terms of coordinates.Therefore the partial differential of displacement is expressed as

where the subscript′j′is the partial differential in terms of x′j.In the elastic strain constant case，the stress is the linear function of the partial differential of displacement as

where Eand the v are the elastic moduli and the Poisson′s ratio，respectively.The substitution of Eq.（28）into Eq.（27）gives the expression of stress as

where Dkij（x′，x）and Skij（x′，x）are the quantities associated with the fundamental solutions given in Appendix.

The solution procedures can be described as below：

（1）Given the geometrical and material information of RVE，use Eqs.（15－17）to construct.

（2）Given global strainεkj，substitute Hlkip，and periodic conditions presented by Eqs.（4－5）into Eq.（14）to obtain the boundary fluctuating displacementand the boundary traction tkp.The relation betweenandεkjcan be expressed by Eq.（21）.

（3）By using Eq.（24），the global elastic pyramids are calculated.

（4）By using Eqs.（27－29）the displacement and stress can be calculated.

It can be seen clearly that the above procedure does not need an iteration process to obtain the solution of the displacement in micro level，which is different from the asymptotic homogenization theory based multi-scale BEM.

2 NUMERICAL RESULTS AND DISCUSSION

2.1 Case of material with periodic hole

To assess the accuracy of the proposed BEM based multi-scale method，a numerical example for the porous material is presented in this section.The stresses predicted by the presented method are compared with the results of the FEM based multi-scale method and the analytical result near the hole.

Considering aporous material with a large number of holes distributed periodically，the dis-tance between the holes nearby is 50μm.Thus，we can use the area highlighted by broken line in Fig.3which is the minimum unit of the microstructure as RVE.The edges of the square RVE is 50μm.

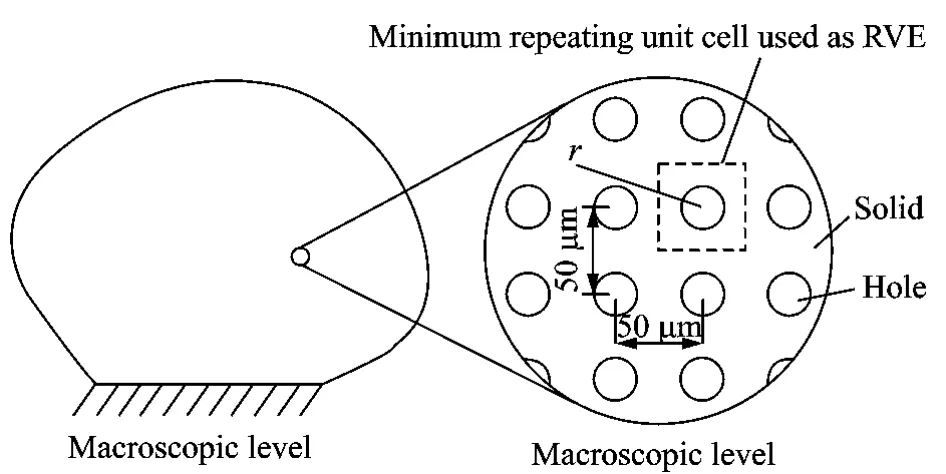
Fig.3 Microstructure of porous material and size of RVE

The finite element based homogenization method is used to generate reference solutions.The meshes for both methods are illustrated in Fig.4.There are a total of 400linear quadrilateral elements and 880nodes for FEM based homogenization method，and a total of 60constant boundary elements for the BEM based multi-scale method.The elastic moduli and Poisson′s ratio for the solid part of porous material denoted in Fig.4are 70GPa and 0.2，respectively.

Fig.4 Boundary element discretization and finite element discretization for RVE

Comparisons are made for the value of components of effective elastic moduli under the plane strain constraint.The effective elastic moduli are defined by the relationship between macroscopic stress and strain as presented by

Because of the symmetry of material，we only need to evaluateQ11andQ23by using the FEM based homogenization method and the proposed BEM based homogenization method.The values of the effective elastic moduli for ten cases with difference radiuses of holes are illustrated in Fig.5.The results indicate that the homogeneous elastic moduli computed by both methods are in a very good agreement.Therefore，it can be concluded that the straightforward multi-scale BEM method gives accurate estimations of the homogenous elastic moduli.

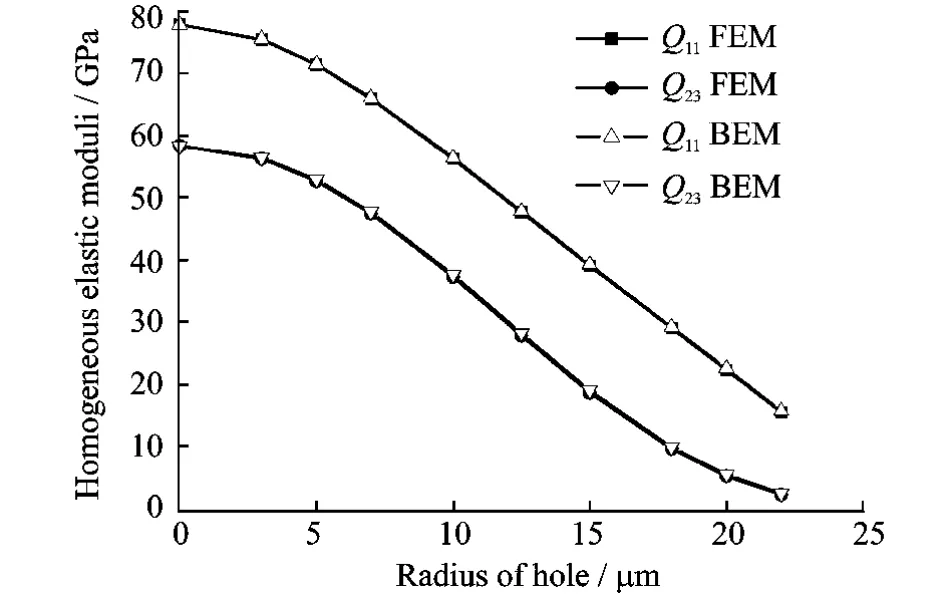
Fig.5 Comparisons of effective elastic constants obtained by BEM and FEM

As indicated previously，the micro-stress field is more important than the homogenous elastic moduli for many applications.Then the ability of the multi-scale BEM to predict the micro-stress field is proved by comparing the micro-stress field estimation by the proposed method with the result predicted by FEM based multi-scale method.Fig.6presents the distribution of micro-stress at the applied macroscopic strain of 0.1along the x1direction.It is seen that exceptσ22，the distribution and the maximum value of the micro-stress predicted by both methods are in a very good agreement.

In fact，the numerical example presented here can be considered as a classical problem in which a large plane with a hole loaded by distributed force Q1and Q2（Fig.7）.Due to the characters of structure and load，the stressesσ11andσ22are distributed symmetrically along X′1and X′2directions，respectively，while the shear stressσ12is distributed symmetrically about the center of the hole.Therefore，the stress concentration will be limited within the area near the hole.According to the formulation of Kirsch G，the stress near the hole is expressed as

Fig.6 Comparisons for micro-stress fields obtained by BEM and FEM

Fig.7 Illustration of large plane with hole loaded by distributed force Q1and Q2

where the coefficients Q1and Q2are respectively equal to the values ofσ11andσ22far away from the hole and can be previously calculated by BEM or FEM based multi-scale method.In this case Q1＝7.455GPa，Q2＝2.57GPa.Then the stress along X′1and X′2axes predicted by analytical formulation are compared with the corresponding results predicted by FEM based and BEM based multi-scale methods（Fig.8）.Fig.8implies that the stresses predicted by FEM based multi-scale method agree well with the analytical results，while the stresses predicted by FEM based multiscale method are quite different from those of the other two methods near the hole.This proves the improved accuracy of BEM based multi-scale method in stress concentration problems.

Through the numerical example presented in this section，we can conclude that the proposed boundary element based multi-scale method is quite accurate for estimating both the homogeneous elastic moduli and the micro-stress filed.

2.2 Case of material with random hole

Fig.8 Comparison of stress predicted by different methods

In order to compare the ability of BEM based multi-scale method with that of FEM based one，RVEs including large number of holes distributed randomly are considered.Indeed，the random distribution will destroy the periodic assumption of the multi-scale method，but by using a variable size RVE technology［23］which is used by many researches，an appropriate size of RVE can be found which will give the approximate solution of elastic properties of material.In this paper，we will not discuss that the appropriate size of RVE can be defined by variable size RVE technology，but only pay attention to the ability of the multi-scale BEM developed here to deal with complicated structure.

Fig.9shows one of the total 100samples and the corresponding meshes for BEM based multiscale method and FEM based one.The elastic moduli and Poisson′s ratio for solid part of material are 70GPa and 0.2，respectively.We can see that the FEM based method need meshes throughout the body.It is difficult to obtain qual-ity meshes for complicated structure.In some cases，the meshes are singular.In the case of BEM based method，only the meshes on boundary are needed，thus it is more convenient for BEM than FEM to construct the mesh.

Fig.9 Illustration of sample and meshes

Fig.10shows the value ofQ11for all the samples.The results implies that the distribution of Q11obtained from the BEM based method proposed here is close to the result from the FEM based method.Fig.10also shows the time for BEM based multi-scale method developed here and the FEM based one to calculate the effective elastic properties of all 100samples.It implies that the BEM based method takes less time than the FEM based method.

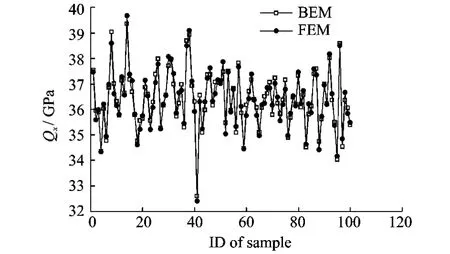
Fig.10 Illustration ofQ11for all the samples（time for BEM＝3 383s，time for FEM＝4 327s）

3 CONCLUSION

The numerical example proves that the presented boundary element based multi-scale method is very accurate and efficient for estimating the homogeneous elastic constants and predicting the fields at microscopic level such as micro-displacement，micro-strain and micro-stress.This can be explained as the result of the analytical feature of BEM.Thanks to the convenient manner of discretization，the boundary element based multiscale method is suitable for modeling the multiphase materials with random microstructure and topology optimization for composite material.Although the formulations of the presented method are derived for the two dimension problem，it also can be easily extended to the three dimension case by changing the fundamental solution to the Kelvin solution.This development will be presented in the authors′forthcoming papers.

APPENDIX

The fundamental solutions used in the boundary integral equations presented in Sections 1.2and 1.4are given as

［1］ Bensoussan A，Lions L J，Papanicolaou G.Asymptotic methods in periodic Media［M］.North Holland：Kluwer Academic，1978.

［2］ Bendsoe M P，Kikuchi N.Generating optimal topologies in structural design using a homogenization method［J］.Computer Methods in Applied Mechanics and Engineering，1988，71（2）：197-224.

［3］ Kikuchi N.Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods［J］.Computer Method in Applied Mechanics and Engineering，1990，83（2）：143-198.

［4］ Nishiwaki S，Frecker M，Min S J，et al.Topology optimization of compliant mechanisms using the homogenization method［J］.International Journal for Numerical Methods in Engineering，1998，42（3）：535-559.

［5］ Ghosh S，Kyunghoon L，Raghavan P.A multi-level computational model for multi-scale damage analysis in composite and porous materials［J］.International Journal of Solids and Structure，2001，38 （14）：2335-2385.

［6］ Raghavan P，Ghosh S.A continuum damage mechanics model for unidirectional composites undergoing interfacial debonding［J］.Mechanics of Materials，2005，37（9）：955-979.

［7］ Ghosh S，Lee K，Moorthy S.Two scale analysis of heterogeneous elastic—Plastic materials with asymptotic homogenisation and Voronoi cell finite element model［J］.Computer Methods in Applied Mechanics and Engineering，1996，132（1）：63-116.

［8］ Kouznetsova V，Geers M G D，Brekelmans W A M.Multi-scale constitutive modeling of heterogeneous materials with a gradient enhanced computational homogenization scheme［J］.International Journal for Numerical Methods in Engineering，2002，54 （8）：1235-1260.

［9］ Kouznetsova V，Geers M G D，Brekelmans W A M.Multi-scale second-order computational homogenization of multi-phase materials：A nested finite element solution strategy［J］.Computer Methods in Applied Mechanics and Engineering，2004，193（51）：5525-5550.

［10］Ladevèze P.Multi-scale modeling and computational strategies for composites［J］.International Journal for Numerical Methods in Engineering，2004，60（1）：233-253.

［11］Dascalu C，Bilbie G，Agiasofitou E K.Damage and size effects in elastic solids：A homogenization approach［J］.International Journal of Solids and Structures，2008，45（2）：409-430.

［12］Sun Jie，Song Yingdong，Gao Xiguang，et al.Prediction of textile fabric reinforced composite properties based on node interpolation cell method［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2011，28（1）：129-136.

［13］Okada H，Fukui Y，Kumazawa N.Homogenization method for heterogeneous material based on boundary element method［J］.Computers and Structures，2001，79（20／21）：1987-2007.

［14］Cruse T A.Numerical solutions in three dimensional elastostatics［J］.International Journal of Solids and Structure，1969，5（12）：1259-1274.

［15］Cruse T A.Recent advances in boundary element analysis method［J］.Computer Method in Applied Mechanics and Engineering，1987，62（3）：227-244.

［16］Rizzo F J.An integral equation approach to boundary value problems of classical elastostatics［J］.Journal of Applied Mathematics，1967，25（1）：83-95.

［17］Sfantos G K，Aliabadi M H.Multi-scale boundary element modeling of material degradation and fracture［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（7）：1310-1329.

［18］Wang H T，Yao Z H.Large scale analysis of mechanical properties in 3-D fiber reinforced composites using a new fast multipole boundary element method［J］.Tsinghua Science ＆Technology，2007，12（5）：562-566.

［19］Kaminski M.Boundary element method homogenization of the periodic linear elastic fiber composites［J］.Engineering Analysis with Boundary Elements，1999，23（10）：815-823.

［20］Koro K，Abe K.A wavelet method for reducing the computational cost of BE-based homogenization anal-ysis［J］.Engineering Analysis with Boundary Elements，2003，27（5）：439-454.

［21］Okada H，Fukui Y，Kumazawa N.A micromechanical analysis of rubber modified epoxy resin［J］.Progress in Experimental and Computational Mechanics in Engineering，2003，243（2）：511-516.

［22］Okada H，Fukui Y，Kumazawa N.Homogenization analysis for particulate composite materials using the boundary element method［J］.Cmes-Computer Modeling in Engineering ＆ Sciences，2004，5（2）：135-149.

［23］Song Y S，Youn J R.Modeling of effective elastic properties for polymer based carbon nanotube composites［J］.Polymer，2006，47（5）：1741-1748.

［24］Buroni F C，Marczak R J.Effective properties of materials with random micro-cavities using special boundary elements［J］.Journal of Materials Science，2008，43（10）：3510-3521.

［25］Ptaszny J，Fedeliński P.Numerical homogenization by using the fast multipole boundary element method［J］.Archives of Civil and Mechanical Engineering，2011，11（1）：181-193.

［26］Michel J C，Moulinec H，Suquet P.Effective properties of composite materials with periodic microstructure：A computational approach［J］.Computer Methods in Applied Mechanics and Engineering，1999，172（1／2）：109-143.

［27］Terada K，Hori M，Kyoya T，Kikuchi N.Simulation of the multi-scale convergence in computational homogenization approaches［J］.International Journal of Solids and Structure，2000，37（16）：2285-2311.

［28］Nemat-Nasser S，Hori M.Micromechanics：Overall properties of heterogeneous materials［M］.Amsterdam：Elsevier Science，1999.

［29］Hazanov S.Hill condition and overall properties of composites［J］.Archive Applied Mechanics，1998，68（6）：385-394.

［30］Kouznetsova V.Computational homogenization for the multi-scale analysis of multi-phase materials［D］.Eindhoven，Netherlands：University of Technology，2002.

［31］Aboudi J，Pindera M J，Arnold S M.Higher-order theory for functionally graded materials［J］.Composites Part B，1999，30（8）：777-832.

［32］Aliabadi M H.The boundary element method［M］.New York：John Wiley ＆Sons，2002.