王亮亮

（吕梁学院，山西 离石033000）

1 预备知识

众所周知，关于子群及其个数的研究在有限群论的研究中是十分重要的.本文主要研究了16阶非交换2群的子群结构.而对于交换的情形，由于子群结构较为简单，不再研究.本文用到的符号都是标准的，均来自文献[1].下面分别用Cn，D2n，Q2n，SD2n和表示n阶循环群，2n阶二面体群，2n阶广义四元数群，2n阶半二面体群，m个n阶循环群的直积.设A，B≤G，若G＝AB且[A，B]＝1，则称G为A，B的中心积，记作G＝A＊B.文中总假设A∩B≠1.接下来，给出定理证明中需要用到的一些引理和定理[2～3].

引理1.1 设G是二元生成的非交换p群且G＝〈a，b〉，则G的极大子群分别是K＝〈Φ（G），a〉与M＝〈Φ（G），bas〉，其中s＝0，1，…，p－1.

引理1.2 设G是三元生成的非交换p群且G＝〈a，b，d〉.则G的极大子群分别是K＝〈Φ（G），a，d〉，Ks＝〈Φ（G），as，d〉以及Kxy＝〈Φ（G），adx，bdy〉，（s，x，y＝0，1，…，p－1）

引理1.3 设G为8阶非交换2群，则G是以下互不同构的群之一:

（I）D8＝〈a，b｜a4＝b2＝1，b－1ab＝a－1〉；

（II）Q8＝〈a，b｜a4＝1，b2＝a2，b－1ab＝a－1〉；

引理1.4 设G为16阶非交换2群，则G是以下互不同构的群之一:

（I）Q16＝〈a，b｜a8＝1，b2＝a4，b－1ab＝a－1〉；

（II）D16＝〈a，b｜a8＝b2＝1，b－1ab＝a－1〉；

（III）SD16＝〈a，b｜a8＝b2＝1，b－1ab＝a3〉；

（IV）G＝〈a，b｜a8＝b2＝1，b－1ab＝a5〉；

（V）G＝〈a，b｜a4＝b4＝1，b－1ab＝a－1〉；

（VI）G＝〈a，b，c｜a4＝b2＝c2＝1，[a，b]＝c，[c，a]＝[c，b]＝1〉；

（VII）D8×C2；

（VIII）Q8×C2；

（IX）G＝〈a，b，c｜a4＝b2＝c2＝1，[b，c]＝a2，[a，b]＝[a，c]＝1〉≅D8＊C4.

2 主要结果

定理2.1 设G为16阶非交换2群Q16＝〈a，b｜a8＝1，b2＝a4，b－1ab＝a－1〉，则G的子群共有11个.分别为:单位元群1；8阶子群有3个:〈a〉，〈a2，b〉，〈a2，ba〉；4阶子群有5个:〈a2〉，〈b〉，〈ba〉，〈ba2〉，〈ba3〉；2阶子群仅有1个:〈a4〉；群G.

证明 显然Φ（G）＝〈a2〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个，分别为H1＝〈a〉，H2＝〈a2，b〉，H3＝〈a2，ba〉.

对于H1而言，由于其循环，因此各阶子群均只有1个，即其2阶子群为〈a4〉，其4阶子群为〈a2〉.

对于H2而言，其定义关系为〈a2，b｜（a2）4＝1，b2＝（a2）2，b－1a2b＝（a2）－1〉，故 Φ（H2）＝〈（a2）2〉且d（H2）＝2.类似，由引理1.1知，H2的极大子群为M1＝〈a2〉，M2＝〈b〉和M3＝〈ba2〉，其中M1，M2，M3均循环且为4阶子群.进一步，显然对于群M1，M2，M3而言，其2阶子群均为〈a4〉.

对于H3而言，其定义关系为〈a2，ba｜（a2）4＝1，（ab）2＝（a2）2，（ba）－1a2（ba）＝（a2）－1〉.故 Φ（H3）＝〈（a2）2〉且d（H3）＝2.类似，由引理1.1知，H3的极大子群为N1＝〈a2〉，和N3＝〈ba3〉，其中N1，N2，N3循环且均为4阶子群，进而，对于群N1，N2，N3而言，其2阶子群均为〈a4〉.

综上可知，该定理得证.

定理2.2 设G为16阶非交换2群D16＝〈a，b｜a8＝b2＝1，b－1ab＝a－1〉，则G的子群共有19个.分别为:单位元群1；8阶子群有3个:〈a〉，〈a2，b〉，〈a2，ba〉；4阶子群有5个:〈a2〉，〈a4，b〉，〈a4，ba〉，〈a4，ba2〉，〈a4，ba3〉；2阶子群有9个:〈a4〉，〈b〉，〈ba〉，〈ba2〉，〈ba3〉，〈ba4〉，〈ba5〉，〈ba6〉，〈ba－1〉；群G.

证明 显然Φ（G）＝〈a2〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个，H1＝〈a〉，H2＝〈a2，b〉，H3＝〈a2，ba〉.

对于H1而言，由于其循环，因此各阶子群均只有1个，即其2阶子群为〈a4〉，其4阶子群为〈a2〉.

对于H2而言，其定义关系为〈a2，b｜（a2）4＝b2＝1，b－1a2b＝（a2）－1〉，故 Φ（H2）＝〈（a2）2〉且d（H2）＝2.类似地，由引理1.1知，H2的极大子群为M1＝〈a2〉，M2＝〈a4，b〉和M3＝〈a4，ba2〉，其中M1循环，M2，M3交换且均为4阶子群.进而，不难知，H2的2阶子群为〈a4〉，〈b〉，〈ba2〉，〈ba4〉，〈ba6〉，

对于H3而言，其定义关系为〈a2，ba｜（a2）4＝（ba）2＝1，（ba）－1a2（ba）＝（a2）－1〉，故 Φ（H3）＝〈（a2）2〉且d（H3）＝2.类似，由引理1.1知，H3的极大子群为N1＝〈a2〉，和N3＝〈a4，ba3〉，其中N1循环，N2，N3交换且均为4阶子群.进而，不难知，H3的2阶子群为〈a4〉，〈ba〉，〈ba3〉，〈ba5〉，〈ba－1〉.

综上可知，该定理得证.

定理2.3 设G为16阶非交换2群SD16＝〈a，b｜a8＝b2＝1，b－1ab＝a3〉，则G的子群共有15个，分别为:单位元群1；8阶子群有3个:〈a〉，〈a2，b〉，〈a2，ba〉；4阶子群有5个:〈a2〉，〈a4，b〉，〈ba〉，〈a4，ba2〉，〈ba3〉；2阶子群有5个:〈a4〉，〈b〉，〈ba2〉，〈ba4〉，〈ba6〉；群G.

证明 易知Φ（G）＝〈a2〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个:H1＝〈a〉，H2＝〈a2，b〉，H3＝〈a2，ba〉.

对于H1而言，由于其循环，因此各阶子群均只有1个，即其2阶子群为〈a4〉，其4阶子群为〈a2〉.

对于H2而言，其定义关系为〈a2，b｜（a2）4＝b2＝1，b－1a2b＝（a2）－1〉，故Φ（H2）＝〈（a2）2〉且d（H2）＝2.类似，由引理1.1知，H2的极大子群为M1＝〈a2〉，M2＝〈a4，b〉和M3＝〈a4，ba2〉，其中M1循环，M2，M3交换且均为4阶子群.进而，不难知，H2的2阶子群为〈a4〉，〈b〉，〈ba2〉，〈ba4〉，〈ba6〉.

对于H3而言，其定义关系为〈a2，b｜（a2）4＝1，b2＝（a2）2，b－1a2b＝（a2）－1〉，故Φ（H3）＝〈（a2）2〉且d（H3）＝2.类似地，由引理1.1知，H3的极大子群为N1＝〈a2〉，和N3＝〈ba3〉，其中N1，N2，N3循环且均为4阶子群.进而，对于群N1，N2，N3而言，其2阶子群均为〈a4〉

综上可知，该定理得证.

定理2.4 设G＝〈a，b｜a8＝b2＝1，b－1ab＝a5〉，则G的子群共有11个，分别为:单位元群1；8阶子群有3个:〈a〉，〈a2，b〉，〈ba〉；4阶子群有5个:〈a2〉，〈a2b〉和〈a4〉×〈b〉；2阶子群有3个:〈a4〉，〈a4b〉和〈b〉；群G.

证明 易知Φ（G）＝〈a2〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个:H1＝〈a〉，H2＝〈a2，b〉，H3＝〈a2，ba〉.注意到（ba）2＝a－2，因此H3＝〈ba〉.

对于H1而言，由于其循环，因此各阶子群均只有1个，即其2阶子群为〈a4〉，其4阶子群为〈a2〉.

对于H2而言，其定义关系为〈a2，b｜（a2）4＝b2＝1，b－1a2b＝a2〉，即H2的8阶交换群〈a2〉×〈b〉≅C4×C2，不难知H2的4阶交换群有3个:〈a2〉，〈a2b〉和〈a4〉×〈b〉；H2的2阶交换群也有3个:〈a4〉，〈a4b〉和〈b〉.

对于H3而言，其定义关系为〈a2，ba｜（a2）4＝1，（ba）2＝a－2，（ba）－1a2（ba）＝a2〉，即H3亦为8阶循环群〈ba〉.因而其各阶子群唯一，即其2阶子群为〈a4〉，其4阶子群为〈a2〉.

综上可知，该定理得证.

定理2.5 设G＝〈a，b｜a4＝b4＝1，b－1ab＝a－1〉，则G的子群共有15个:单位元群1；8阶子群有3个:〈a，b2〉，〈a2，b〉，〈a2，ba〉；4阶子群有7个:〈a〉，〈ab2〉，〈b〉，〈ba2〉，〈ba〉，〈ba3〉，〈a2〉×〈b2〉；2阶子群有3个:〈a2〉，〈b2〉，〈a2b2〉；群G.

证明 易知Φ（G）＝〈a2，b2〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个:H1＝〈a，b2〉，H2＝〈a2，b〉，H3＝〈a2，b2，ba〉，注意到（ba）2＝baba＝b2b－1aba＝b2a－1a＝b2，因此H3＝〈a2，ba〉.

对于H1而言，由于（b2）－1ab2＝b－1b－1abb＝b－1a－1b＝（b－1ab）－1＝a，因此H1的定义关系为〈a，b2｜a4＝（b2）2＝1，（b2）－1ab2＝a〉，即H1＝〈a〉×〈b2〉≅C4×C2，因而易知H1的2阶子群有3个:〈a2〉，〈b2〉，〈a2b2〉；H1的4阶子群有3个:〈a〉，〈ab2〉，〈a2〉×〈b2〉.对于H2而言，由于b－1a2b＝a－2＝a2，因此H2的定义关系为〈a2，b｜（a2）2＝b4＝1，b－1a2b＝a2〉，即H2＝〈b〉×〈a2〉≅C4×C2，易知H2的2阶子群有3个:〈a2〉，〈b2〉，〈a2b2〉；H2的4阶子群有3个:〈b〉，〈ba2〉，〈a2〉×〈b2〉；对于H3而言，由于（ba）－1a2（ba）＝a－1b－1aba＝a2，因此，H3的定义关系为〈a2，ba｜（a2）2＝（ba）4＝1，（ba）－1a2（ba）＝a2〉，即H3＝〈ba〉×〈ab2〉≅C4×C2，从而易知H3的2阶子群有3个:〈a2〉，〈（ba）2〉，〈a2（ba）2〉，又注意到baba＝b2b－1aba＝b2a－1a＝b2，因此，〈（ba）2〉＝〈b2〉，〈a2（ba）2〉＝〈a2b2〉H3的4阶子群有3个:〈ba〉，〈ba3〉，〈（ba）2〉×〈a2〉＝〈a2〉×〈b2〉.

综上可知，该定理得证.

定理2.6 设G＝〈a，b，c｜a4＝b2＝c2＝1，[a，b]＝c，[c，a]＝[c，b]＝1〉，则G的子群共有23个:单位元群1；8阶子群有3个:〈a〉×〈c〉，〈a2〉×〈c〉×〈b〉，〈ba〉×〈c〉；4阶子群有11个:〈a〉，〈ac〉，〈a2〉×〈c〉，〈a2〉×〈b〉，〈b〉×〈c〉，〈a2b〉×〈a2c〉，〈a2〉×〈bc〉，〈b〉×〈ac〉，〈c〉×〈ab〉，〈ba〉，〈bac〉；2阶子群有七个:〈a2〉，〈c〉，〈a2c〉，〈b〉，〈a2b〉，〈bc〉，〈a2bc〉，〈ba〉；群G.

证明 显然Φ（G）＝〈a2，c〉且d（G）＝2.由引理1.1知，G的极大子群有3个，即8阶子群有3个:H1＝〈a2，c，a〉＝〈a，c〉，又注意到[c，a]＝1，因此H2＝〈a〉×〈c〉≅C4×C2，H2＝〈a2，c，b〉，又注意到[c，a]＝[c，b]＝1，因此H2＝〈a2〉×〈c〉×〈b〉≅C2×C2×C2，H2＝〈a2，c，ba〉.

由于（ba）2＝baba＝aa－1b－1aba＝a2c，因此H3＝〈ba〉×〈c〉≅C4×C2，由于H1，H2，H3均为交换群，因此容易得:H1的2阶子群有3个:〈a2〉，〈c〉，〈a2c〉；H1的4阶子群有3个:〈a〉，〈ac〉，〈a2〉×〈c〉；H2的2阶子群有7个:〈a2〉，〈b〉，〈c〉，〈a2b〉，〈a2c〉，〈bc〉，〈a2bc〉；H2的4阶子群亦有7个:〈a2〉×〈c〉，〈a2〉×〈b〉，〈b〉×〈c〉，〈a2b〉×〈a2c〉，〈a2〉×〈bc〉，〈b〉×〈ac〉，〈c〉×〈ab〉；H3的2阶子群有3个:〈（ba）2〉＝〈a2c〉，〈c〉，〈a2〉；H3的4阶子群有3个:〈ba〉，〈bac〉，〈（ba）2〉×〈c〉＝〈a2〉×〈c〉.

综上可知，该定理得证.

定理2.7 设

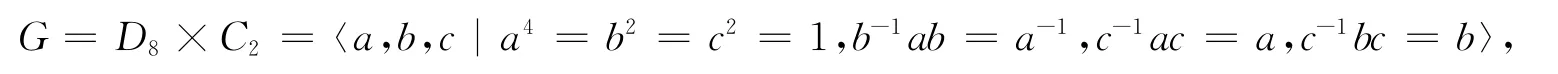
则G的子群共有35个:单位元群1；8阶子群有7个:〈a〉×〈c〉，〈a2〉×〈b〉×〈c〉，〈a2〉×〈ba〉×〈c〉，〈a，b〉，〈a，bc〉，〈ac，b〉，〈ac，bc〉；4阶子群有15个:〈a〉，〈ac〉，〈a2〉×〈c〉，〈a2〉×〈b〉，〈b〉×〈c〉，〈a2b〉×〈a2c〉，〈a2〉×〈bc〉，〈b〉×〈a2c〉，〈c〉×〈a2b〉，〈a2〉×〈ba〉，〈ba〉×〈c〉，〈ba3〉×〈a2c〉，〈a2〉×〈bac〉，〈ba〉×〈a2c〉，〈c〉×〈ba3〉；2阶子群有11个:〈a2〉，〈c〉，〈a2c〉，〈b〉，〈a2b〉，〈bc〉，〈a2bc〉，〈ba〉，〈ba3〉，〈bac〉，〈ba3c〉；群G.

证明 显然此时Φ（G）＝〈a2〉且d（G）＝3.由引理1.2知，G有7个极大子群，即有7个8阶子群:K1＝〈a，c〉，K2＝〈a2，b，c〉，K3＝〈a2，ba，c〉，K4＝〈a，b〉，K5＝〈a，bc〉，K6＝〈ac，b〉，K7＝〈ac，bc〉.注意到[c，a]＝1，因此K1交换，且K1＝〈a〉×〈c〉≅C4×C2.由于[a2，b]＝[a2，c]＝[b，c]＝1，因此K2交换，且K2＝〈a2〉×〈b〉×〈c〉≅C2×C2×C2.类似，由于[a2，ba]＝[a2，c]＝[ba，c]＝1，因此可得K3交换，且K3＝〈a2〉×〈ba〉×〈c〉≅C2×C2×C2.

由于K1，K2，K3交换，因此易知K1的4阶子群有3个:〈a〉，〈ac〉，〈a2〉×〈c〉.K1的2阶子群有3个:〈a2〉，〈c〉，〈a2c〉；K2的4阶子群有7个:〈a2〉×〈b〉，〈a2〉×〈c〉，〈b〉×〈c〉，〈a2b〉×〈a2c〉，〈a2〉×〈bc〉，〈b〉×〈a2c〉，〈c〉×〈a2b〉；K2的2阶子群有7个:〈a2〉，〈b〉，〈c〉，〈a2b〉，〈a2c〉，〈bc〉，〈a2bc〉；K3的4阶子群有7个:〈a2〉×〈ba〉，〈a2〉×〈c〉，〈ba〉×〈c〉，〈ba3〉×〈a2c〉，〈a2〉×〈bac〉，〈ba〉×〈a2c〉，〈c〉×〈ba3〉；K3的2阶子群有7个:〈a2〉，〈ba〉，〈c〉，〈ba3〉，〈a2c〉，〈bac〉，〈ba3c〉.

对于K4，K5，K6，K7而言，分析各自定义关系易知均同构于D8，因此，通过计算有K4有5个2阶子群:〈a2〉，〈a2b〉，〈b〉，〈ba〉，〈ba3〉；3个4阶子群:〈a〉，〈a2〉×〈b〉，〈a2〉×〈ba〉；K5有5个2阶子群:〈a2〉，〈a2bc〉，〈bc〉，〈bca〉，〈bca3〉；3个4阶子群:〈a〉，〈a2〉×〈bc〉，〈a2〉×〈bca〉；K6有5个2阶子群:〈（ac）2〉×〈a2〉，〈a2b〉，〈b〉，〈bac〉，〈ba3c〉；3个4阶子群:〈ac〉，〈a2〉×〈b〉，〈a2〉×〈bac〉；K7有5个2阶子群:〈a2〉，〈a2bc〉，〈bc〉，〈bca〉，〈bca3〉；3个4阶子群:〈ac〉，〈a2〉×〈bc〉，〈a2〉×〈bca〉.

综上可知，该定理得证.

定理2.8 设

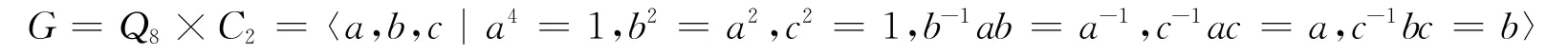
则G的子群共有19个:单位元群1；8阶子群有7个:〈a，c〉，〈b，c〉，〈ba，c〉，〈a，b〉，〈a，bc〉，〈ac，b〉，〈ac，bc〉；4阶子群有7个:〈a〉，〈ac〉，〈a2〉×〈c〉，〈b〉，〈bc〉，〈ba〉，〈bac〉；2阶子群有3个:〈a2〉，〈c〉，〈a2c〉；群G.

证明 显然此时d（G）＝3且Φ（G）＝〈a2〉.由引理1.2知，G有7个极大子群，即有7个8阶子群:K1＝〈a，c〉，K2＝〈a2，b，c〉＝〈b，c〉，K3＝〈ba，c〉，K4＝〈a，b〉，K5＝〈a，bc〉，K6＝〈ac，b〉，K7＝〈ac，bc〉.因为[a，b]＝a2，[c，a]＝[c，b]＝1，所以不难知K1，K2，K3交换，K4，K5，K6，K7非交换.下面逐一来分析Ki，其中i＝1，2，…，7的子群结构.

对于Ki，其中i＝1，2，3而言，显然Ki≅C4×C2，K1的4阶子群有3个:〈a〉，〈ac〉，〈a2〉×〈c〉，其2阶子群亦有3个:〈a2〉，〈c〉，〈a2c〉；K2的4阶子群有3个:〈b〉，〈bc〉，〈b2〉×〈c〉＝〈a2〉×〈c〉，2阶子群亦有3个:〈b2〉＝〈a2〉，〈c〉，〈a2c〉；K3的4阶子群有3个:〈ba〉，〈bac〉，〈（ba）2〉×〈c〉＝〈a2〉×〈c〉，其2阶子群亦有3个:〈（ba）2〉＝〈a2〉，〈c〉，〈a2c〉.

对于K4，K5，K6，K7而言，分析定义关系易知均同构于Q8.因此易知K4有1个2阶子群〈a2〉，3个4阶子群〈a〉，〈b〉，〈ba〉；K5有1个2阶子群〈a2〉，3个4阶子群〈a〉，〈bc〉，〈bca〉；K6有1个2阶子群〈（ac）2〉＝〈a2〉，3个4阶子群〈ac〉，〈b〉，〈bac〉；K7有1个2阶子群〈（ac）2〉＝〈a2〉，3个4阶子群〈ac〉，〈bc〉，〈bcac〉＝〈bac2〉＝〈ba〉.

综上可知，该定理得证.

定理2.9 设G＝〈a，b，c｜a4＝b2＝c2＝1，[b，c]＝a2，[a，b]＝[a，c]＝1〉≅D8×C4，则G的子群共有23个:单位元群1；8阶子群有7个:〈a〉×〈c〉，〈b，c〉，〈ba，c〉，〈a〉×〈b〉，〈a，bc〉＝〈a〉×〈bca〉，〈ac，b〉，〈ac，bc〉；4阶子群有7个:〈a〉，〈ac〉，〈a2〉×〈c〉，〈bc〉，〈ba〉，〈a2〉×〈b〉，〈a2〉×〈bca〉；2阶子群有7个:〈a2〉，〈c〉，〈a2c〉，〈b〉，〈a2b〉，〈bca〉，〈bca3〉；群G.

证明 显然此时d（G）＝3且Φ（G）＝〈a2〉.由引理1.2知，G有7个极大子群，即有7个8阶子群:K1＝〈a，c〉，K2＝〈b，c〉，K3＝〈ba，c〉，K4＝〈a，b〉，K5＝〈a，bc〉，K6＝〈ac，b〉，K7＝〈ac，bc〉.由于[c，a]＝1，因此K1为8阶交换子群.即K1＝〈a〉×〈c〉≅C4×C2.因而K1有3个4阶子群:〈a〉，〈ac〉，〈a2〉×〈c〉；有3个2阶子群:〈a2〉，〈c〉，〈a2c〉；对于K2而言，其有如下定义关系:〈b，c｜b2＝c2＝1，[b，c]＝a2〉，注意到d（K2）＝2且Φ（K2）＝〈a2〉，因此由引理1.1知，K2有3个极大子群，即有3个4阶子群:K21＝〈a2，b〉，K22＝〈a2，c〉和K23＝〈a2，bc〉.由于（bc）2＝bcbc＝b－1c－1bc＝a2且[a，b]＝[a，c]＝1，因此K21，K22交换但不循环，K23为4阶循环群.从而易得K2的2阶子群分别为:〈a2〉，〈b〉，〈a2b〉，〈c〉，〈a2c〉.对于K3而言，其有如下定义关系:〈ba，c｜（ba）4＝c2＝1，[ba，c]＝（ba）2〉，即K3≅D8，因此计算知，K3有五个2阶子群:〈（ba）2〉＝〈a2〉，〈a2c〉，〈c〉，〈cba〉，〈cba3〉；3个4阶子群:〈ba〉，〈a2〉×〈c〉，〈a2〉×〈cba〉.对于K4而言，注意到[a，b]＝1，因此K4为8阶交换子群.即K4＝〈a〉×〈b〉≅C4×C2.因而K4有3个4阶子群:〈a〉，〈ab〉，〈a2〉×〈b〉；有3个2阶子群:〈a2〉，〈b〉，〈a2b〉.对于K5而言，由于（bc）2＝bcbc＝b－1c－1bc＝a2，因此其有如下定义关系:〈a，bc｜a4＝1，（bc）2＝a2，[bc，a]＝1〉，即K5亦为8阶交换群.因此K5的4阶子群为〈a〉，〈bc〉，〈a2〉×〈bca〉.K5的2阶子群为〈a2〉，〈bca〉，〈bca3〉.对于K6而言，由于（ac）2＝a2且[ac，b]＝a2＝（ac）2，K6有如下定义关系:〈ac，b｜（ac）4＝b2＝1，[ac，b]＝（ac）2〉，即K6≅D8.因此K6有5个2阶子群:〈（ac）2〉＝〈a2〉，〈a2b〉，〈b〉，〈bac〉，〈bca3〉；3个4阶子群:〈ac〉，〈a2，b〉，〈a2，bac〉.

对于K7而言，由于（ac）4＝a2，（bc）2＝a2，[ac，bc]＝a2，因此K7有如下定义关系:〈ac，bc｜（ac）4＝1，（bc）2＝（ac）2，[ac，bc]＝（ac）2〉，即K7≅D8.因此K7有1个2阶子群〈（ac）2〉＝〈a2〉，3个4阶子群〈ac〉，〈bc〉，〈bcac〉＝〈ba〉.

综上可知，该定理得证.

[1]徐明曜.《有限群导引》（上册）[M].第二版.北京:科学出版社，1999

[2]孙秀娟.指数为p2的子群均交换的有限p群[D].临汾:山西师范大学，2006

[3]徐明曜，曲海鹏.有限p群[M].北京:北京大学出版社，2010