刘 敏，赵 彬

（陕西师范大学 数学与信息科学学院，陕西 西安710062）

偏序集理论在数学以及相关学科领域有广泛的应用．但由于分明偏序仅能刻画元素之间的大小关系而不能反映其相对大或小的程度，因此自从Zadeh提出模糊集的概念以来许多学者致力于将分明的序关系推广到多值的情形．近年来，由于Ω－范畴理论［1－5］、量化Domain理论［6－10］的发展，一种新的模糊偏序［6，8，11］被提出．分明偏序集理论中的许多重要概念与结论，相继被推广到模糊偏序集的框架之下．

完备格同余关系是偏序集理论中的一个重要概念，它与偏序集上的闭包算子、闭包系统等概念有密切的关系．因此，在模糊偏序集的理论框架下能否引入模糊完备格同余关系，它与模糊偏序集中已有的闭包算子等概念之间是否存在如分明情形下的关系是一个值得研究的问题．基于以上情况，本文在模糊完备格中引入模糊完备格同余关系，并进一步讨论它与模糊闭包算子之间的关系．

1 预备知识

文中L均表示一个Frame［12］．用1、0分别表示L的最大元与最小元．为了统一概念，下面回顾有关模糊偏序集的概念和结论．相关内容来自文献［6－11］．

定义1［6－7，11］设X是一个集合，称映射e：X×X→L为X上的模糊偏序，如果e满足：

（E1）∀x∈X，e（x，x）＝1；

（E2）∀x、y、z∈X，e（x，y）∧e（y，z）≤e（x，z）；

（E3）∀x、y∈X，e（x，y）＝e（y，x）＝1蕴含x＝y，此时，称序对（X，e）为一个模糊偏序集．

设（X，e）是一个模糊偏序集，定义X上的二元关系≤e为x≤ey当且仅当e（x，y）＝1，则（X，≤e）是一个偏序集．通常记由模糊偏序集（X，e）诱导的偏序集（X，≤e）为X0．记X0中的并交运算为∨，∧．

例1 下面给出本文将要用到的模糊偏序集的例子：

（1）定义eL：L×L→L为∀α、β∈L，eL（α，β）＝α→β，则（L，eL）是模糊偏序集；

（2）设（X，e）是模糊偏序集，Y⊆X，则（Y，e｜Y×Y）也是模糊偏序集，称为X的子模糊偏序集，简记为（Y，e）；

（3）设X是一个集合，（Y，eY）是一个模糊偏序集，记X到Y的所有映射之集为YX．定义sub：YX×YX→L为：∀f、g∈YX，sub（f，g）g（x）），则（YX，sub）是模糊偏序集．

定义2［8］设（X，e）是一个模糊偏序集，A∈LX，a∈X，

（ⅰ）∀x∈X，A（x）≤e（x，a）；

（ⅰ）∀x∈X，A（x）≤e（a，x）；

由（E3）可知，若上确界（或下确界）存在则必唯一．

注1［8］设（X，e）是一个模糊偏序集，A∈LX，a∈X，则

（3）定义↓A∈LX为：∀x∈X，（↓A）（x）＝（A（y）∧e（x，y）），则A存在当且仅当↓A存在，此时

定义3［8，10］设（X，e）是一个模糊偏序集，若∀A∈LXA和A存在，则称X是模糊完备格．

注2［7，10］设（X，e）是一个模糊偏序集，则以下条件等价：

（1）（X，e）是模糊完备格；

（2）∀A∈LXA存在；

（3）∀A∈LXA存在．

易证，若（X，e）是模糊完备格，则X0是完备格．∀A⊆X0，∨A＝χA，χA：X→L是A的特征函数，当x∈A时χA（x）＝1；当x∉A时χA（x）＝0．

设f：X→Y是集合X到Y的一个映射，定义fL→：LX→LY为 ∀A∈LX，y∈Y，fL→（A）（y）＝∨｛A（x）｜x∈X，f（x）＝y｝．

定义4 设f：X→Y是模糊偏序集（X，eX）、（Y，eY）之间的映射：

（1）如果∀a、b∈X，eX（a，b）≤eY（f（a），f（b）），则称映射f保模糊序；

（2）如果∀a、b∈X，eX（a，b）＝eY（f（a），f（b）），则称映射f是模糊序嵌入；

（3）如果f是满的模糊序嵌入，则称f是模糊序同构，此时称X和Y是同构的，记作X≅Y；

（4）如果∀A∈LX，f（A）＝fL→（A）则称f保模糊并．

注3 设f：X→Y是模糊偏序集（X，eX）、（Y，eY）之间的映射：

（1）若f保模糊序，则f：X0→Y0是保序映射；

（2）若f保模糊并，则f保模糊序且f：X0→Y0是保并映射．

定义5［3］设（X，e）是一个模糊偏序集，

（1）称X是tensor完备的，如果∀x∈X，α∈L，存在α⊗x∈X，使得∀y∈X，e（α⊗x，y）＝α→e（x，y）；

（2）称X是cotensor完备的，如果∀x∈X，α∈L，存在αx∈X，使得∀y∈X，e（y，αx）＝α→e（y，x）．

设x∈X，α∈L，用xα表示从X到L将x映为α，其余映为0的映射．由定义可知，α⊗x＝xα，α x＝xα．因此，完备的模糊偏序集是tensor完备和cotensor完备的．若（X，e）是一个模糊完备格，则∀A∈LX，A＝（A（X）⊗x）；∀｛xi｜i∈I｝⊆X，y∈X，e（xi，y）．有关tensor完备和cotensor完备的模糊偏序集的进一步的性质可参考文献［3，5］．

定义6［13－14］设f：X→X是模糊偏序集（X，e）上保模糊序的映射，如果∀x∈X，e（x，f（x））＝e（f（f（x）），f（x））＝1，则称f是模糊闭包算子．

记模糊偏序集（X，e）上的全体模糊闭包算子之集为COL（X）．

若f是模糊偏序集（X，e）上的模糊闭包算子，则f是X0上的闭包算子，且∀x、y∈X，e（x，f（y））＝e（f（x），f（y））．

2 模糊完备格上的模糊同余关系

下面引入模糊完备格同余关系的概念，并讨论它与模糊闭包算子的关系．

定义7［11］设X是一个非空集合，R：X×X→L是X上的L－关系，若对任意的x、y、z∈X，R满足：

（1）R（x，x）＝1；

（2）R（x，y）＝R（y，x）；

（3）R（x，y）∧R（y，z）≤R（x，z），则称R是X上的一个L－等价关系．

定义8 设（X，e）是一个模糊完备格，R：X×X→L是X上的一个L－等价关系，若对任意的x、y、z∈X，R满足：

（2）e（x，y）∧R（x，z）≤R（y，y∨z），则称R是X上的一个模糊完备格同余关系．

记模糊完备格（X，e）上的全体模糊完备格同余关系之集为CRL（X）．

命题1 设f：X→Y是模糊完备格（X，eX）和（Y，eY）之间保模糊并的映射．定义Rf：X×X→L为：∀a、b∈X，Rf（a，b）＝eY（f（a），f（b））∧eY（f（b），f（a）），则Rf是模糊完备格同余．

证明 由定义容易验证Rf是L－等价关系．

（1）由于∀x∈X、t∈Y，

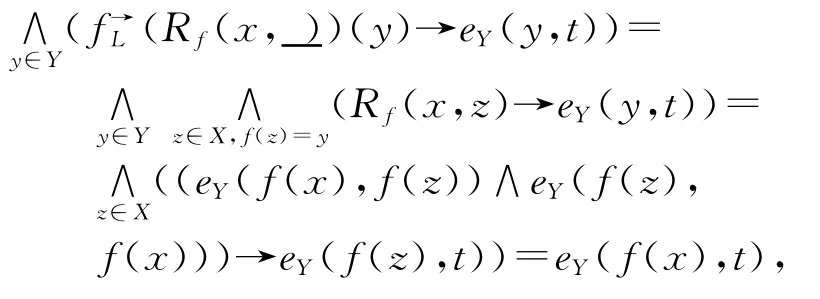
（2）∀a、b、c∈X，eX（a，b）∧Rf（a，c）≤eY（f（a），f（b））∧（eY（f（a），f（c））∧eY（f（c），f（a）））≤eY（f（c），f（b））∧ey（f（b），f（b））＝ey（f（b）∨f（c），f（b））＝eY（f（b∨c），f（b））∧eY（f（b），f（b∨c））＝Rf（b，b∨c）．

因此Rf是模糊完备格同余．

命题2 设j：X→X是模糊完备格（X，e）上的一个模糊闭包算子．定义Rj：X×X→L为：∀x、y∈X，Rj（x，y）＝e（j（x），j（y））∧e（j（y），j（x）），则Rj是X上的模糊完备格同余关系．

证明 （1）容易验证Rj是L－等价关系．

（2）因为∀y∈X，Rj（x，y）＝e（j（x），j（y））∧e（j（y），j（x））≤e（y，j（x）），并且

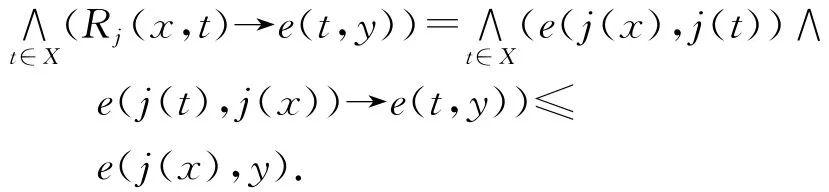
（3）∀x、y、z∈X，e（x，y）∧Rj（x，z）＝e（x，y）∧e（j（x），j（z））∧e（j（z），j（x））≤e（j（x），j（y））∧e（j（z），j（x））≤e（j（z），j（y））＝e（y，j（y））∧e（z，j（y））≤e（y∨z，j（y））＝e（j（y∨z），j（y））＝Rj（y，y∨z）．

由（1）—（3）可见Rj是模糊完备格同余．

命题3 设（X，e）是一个模糊完备格，R∈CRL（X），定义映射jR：X→X为：∀x∈X，jR（x）＝R（x，＿），则jR是模糊闭包算子．

证明 对任意的x、y、z∈X，有

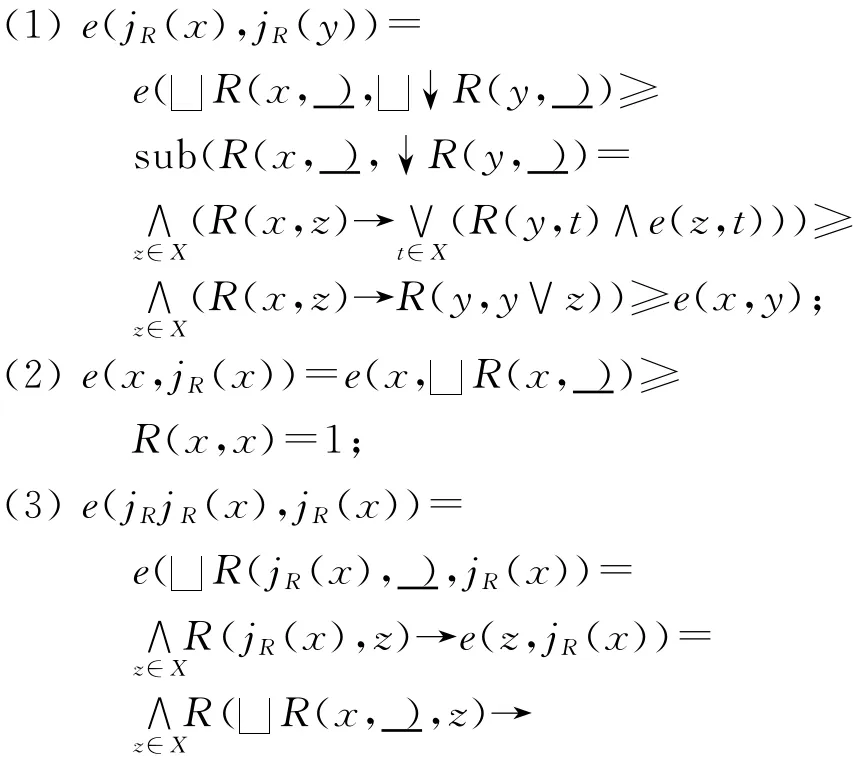
由上知jR是模糊闭包算子．

引理1 设（X，e）是模糊完备格，则

（1）映射φ：CRL（X）→COL（X）（R jR）保模糊序；

（2）映射ψ：COL（X）→CRL（X）（j Rj）保模糊序．

证明 （1）设R1、R2∈CRL（X），则

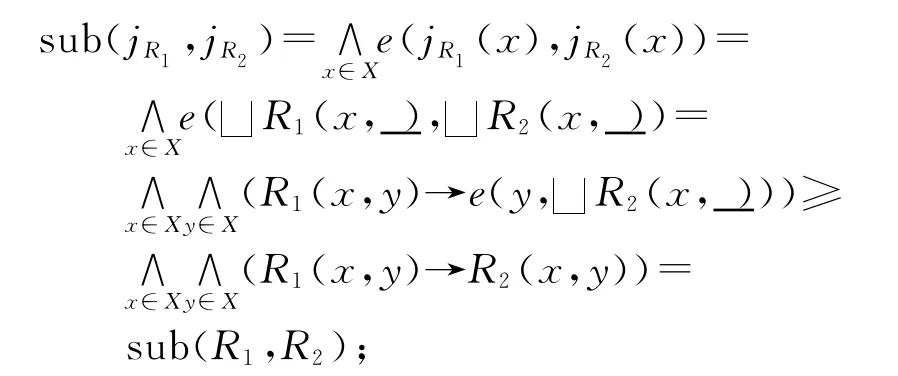
（2）设j1、j2∈COL（X），则

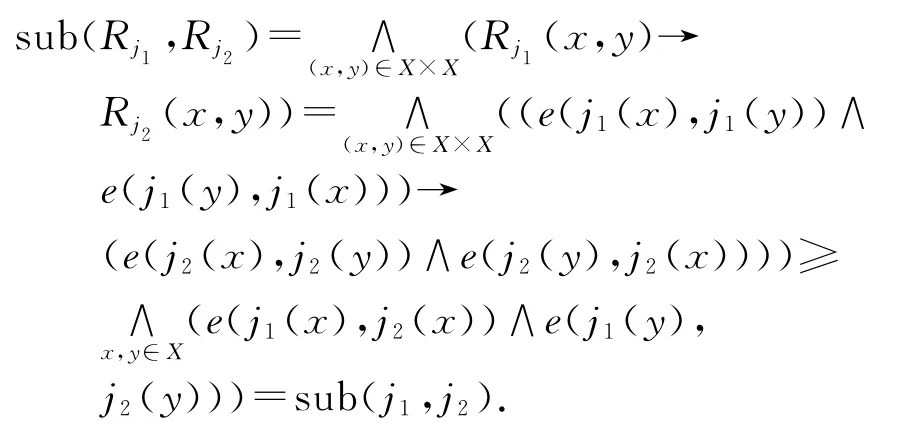
定理1 设（X，e）是模糊完备格，j∈COL（X），R∈CRL（X），则

（1）jRj＝j；（2）RjR＝R．证明 （1）由命题2的证明可知∀x∈X，

（2）∀x∈X，一方面：

另一方面：

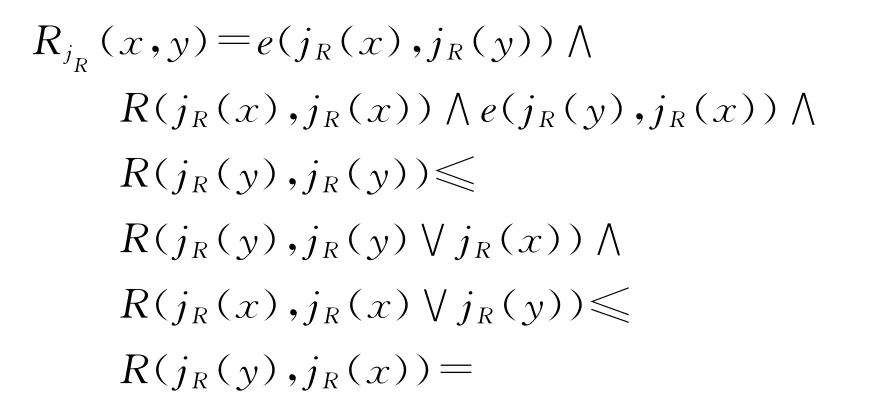
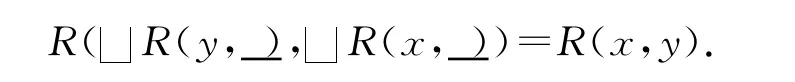
所以，RjR＝R．

定理2 设（X，e）是模糊完备格，则COL（X）≅CRL（X）．

证明 由引理1和定理1可以证明．

3 模糊完备格同余的商

下面引入模糊完备格同余的商概念，并讨论它的有关性质．

命题4 设R是模糊完备格（X，e）上的模糊同余关系．记X／R＝｛R（x，＿）｜x∈X｝．定义映射

（1）（X／R，eR）是模糊完备格，对于A∈LX／R，其中

（2）投射p：X→X／R（x R（x，＿））保模糊并．

证明 （1）易知eR满足（E1）和（E2），下面证明eR满足（E3）：设eR（R（x，＿），R（y，＿））＝eR（R（y，＿），R（x，＿））＝1，则jR（x）＝jR（y）．从而对任意的z∈X，

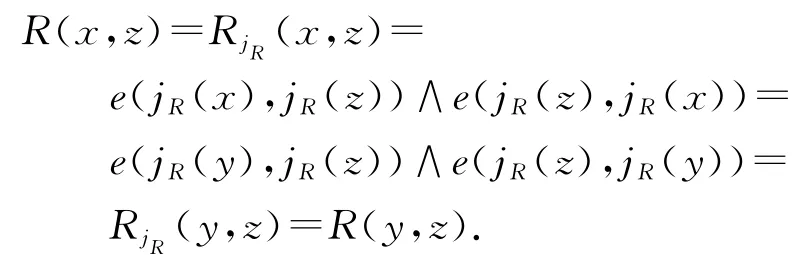
所以eR是模糊序．

设A∈LX／R，记

R（x，＿）），则对任意的z∈X，

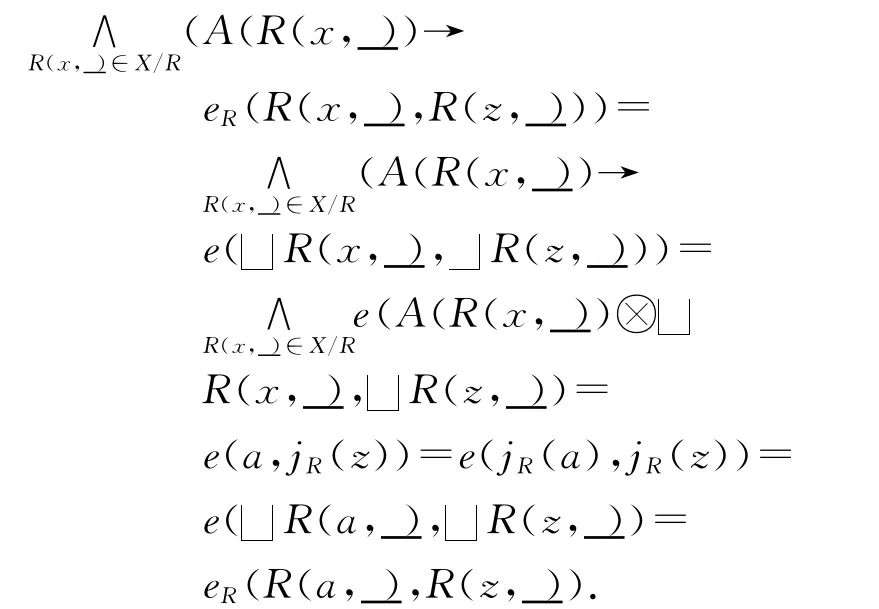
（2）设A∈LX．由于p（A）＝R（A，＿），pL→（A）＝R（a，＿），其中

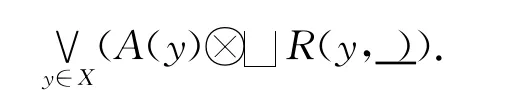
另一方面，由于∀t∈X，

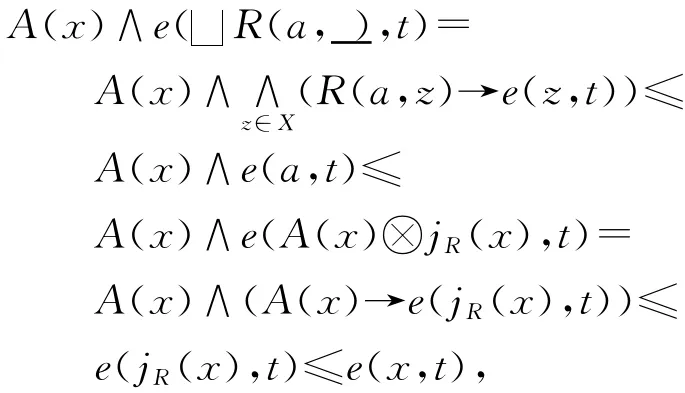
称（X／R，eR）是模糊完备格X模同余关系R的商，简称为同余关系R的商．

定理3 设f：X→Y是模糊完备格（X，eX）和（Y，eY）之间保模糊并的满射，则

（X／Rf，eRf）≅（Y，eY）．

证明 定义映射φ：X／Rf→Y（Rf（x，＿）f（x）），则

（1）φ是良定的：若Rf（a，＿）＝Rf（b，＿），则1＝Rf（a，b）＝eY（f（a），f（b））∧eY（f（b），f（a）），因此f（a）＝f（b）．

（2）φ是满射：由f是满射可知φ是满射．

（3）φ是模糊序嵌入：∀a、b∈X，一方面：

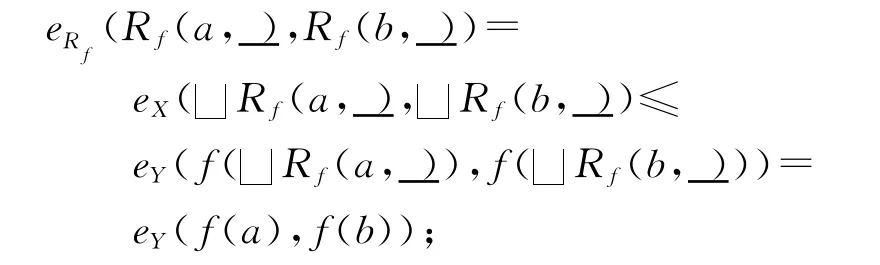
另一方面：

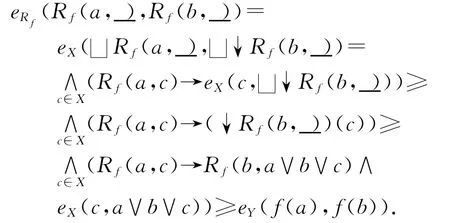
定理4 设j：X→X是模糊完备格（X，e）上的模糊闭包算子，则（j（X），e）≅（X／Rj，eRj）．

证明 定义映射φ：X／Rj→j（X）（Rj（x，＿）j（x）），则可验证φ是模糊序同构．

4 结语

本文给出了模糊完备格同余的概念，并讨论了它与模糊闭包算子的关系．研究了模糊完备格同余的商的性质．这为进一步讨论模糊完备格的其他性质提供了工具．有时人们将模糊偏序集定义在更一般的完备剩余格上，因而当L是完备剩余格时如何恰当地定义模糊完备格同余，以及它的相关应用有待进一步研究．

［1］Wagner K R．Solving recursive domain equations with enriched categories［D］．Pittsburgh：Carnegie－Mellon University，School of Computer Science，1994．

［2］Wagner K R．Liminf convergence inΩ－categories［J］．Theoretical Computer Science，1997，184（1／2）：61－104．

［3］Lai Hongliang，Zhang Dexue．Many－valued complete distributivity［DB／OL］．（2006－05－12）［2012－01－02］．http：／／arxiv．org／abs／math／0603590．

［4］Lai Hongliang，Zhang Dexue．Complete and directed completeΩ－categories［J］．Theoretical Computer Science，2007，388（1／3）：1－25．

［5］赖洪亮．Ω－范畴序结构性质的研究［D］．成都：四川大学数学学院，2007．

［6］Fan Lei．A new approach to quantitative domain theory［J］．Electronic Notes in Theoretical Computer Science 2001，45：77－87．

［7］Yao Wei．Quantitative domains via fuzzy sets：Part I：continuity of fuzzy directed complete posets［J］．Fuzzy Sets and Systems，2010，161（7）：983－987．

［8］Zhang Qiye，Fan Lei．Continuity in quantitative domains［J］．Fuzzy Sets and Systems，2005，154（1）：118－131．

［9］樊磊．Domain理论中若干问题的研究［D］．北京：首都师范大学数学科学学院，2001．

［10］Zhang Qiye，Xie Weixian，Fan Lei．Fuzzy complete lattices［J］．Fuzzy Sets and Systems，2009，160（16）：2275－2291．

［11］Bělohlávek R．Fuzzy relational systems：Foundations and principles［M］．New York：Kluwer Academic Publishers，Plenum Publishers，2002：203－213．

［12］郑崇友，樊磊，崔宏斌．Frame与连续格［M］．北京：首都师范大学出版社，1994：84－91．

［13］Yao Wei，Lu Lingxia．Fuzzy Galois connections on fuzzy posets［J］．Mathematical Logic Quarterly，2009，55（1）：105－112．

［14］Guo Lankun，Zhang Guoqiang，Li Qingguo．Fuzzy closure systems on L－ordered sets［J］．Mathematical Logic Quarterly，2011，57（3）：281－291．