李旭 张正娣 毕勤胜

(江苏大学理学院,镇江 212013)

1 引言

许多实际模型都会涉及到多时间尺度问题[1,2],这种多时间尺度因素不仅来自于真实时间上的快慢效应,同时也可能来自于几何尺寸上的尺度效应,还有诸如反应系统结构效应、系统内部的物理效应等等,通过无量纲化后,在相应的数学模型中形成状态变量在变化速率上的差异,此类系统也可称为快慢耦合系统.如Oregonator化学反应模型中存在的不同量级反应速度的催化和自催化过程[3];在生物细胞中,快速的代谢过程可以结合到很慢的遗传变化上[4];各种飞行器涉及高速的旋转动力学与相对较慢的平移动力学的组合;其他还有诸如带有饱和吸收器的激光系统[5,6]、神经动力学[7]等领域都会涉及多时间尺度问题.一般来说,快慢系统的周期振荡通常表现为由具有相对较大振幅的振荡和近似简谐振动的微幅振荡组合而成的,这种周期运动被称为混合模态振动[8,9],通常用符号LS表示,其中L和S分别表示每一周期运动内大幅振动和微幅振荡的次数,而连接快慢两过程的行为一般被称为簇发.簇发现象在神经元模型中已经被广泛研究,对于一般的光滑快慢系统,Izhikevich[10]对低维情形下的各种簇发现象及其分岔机制做了很好的总结,而对于高维系统和非光滑系统中的不同尺度效应及其分岔机制,目前还有很多问题值得研究.

作为一个经典的混沌电路,蔡氏电路[11]由于结构简单在实验中能很方便地加以搭建,同时也具有如阵发混沌[12]、加周期分岔[13]等非常丰富的动力学行为,因而引起了广泛的关注.为深入探讨非线性系统的复杂性及相应的产生机理,许多学者基于经典蔡氏电路,通过相应的修改或扩展,建立了一系列的广义蔡氏电路,并取得了大量的成果.例如,Stouboulos等[14]和Kolipanos等[15]应用蔡氏二极管替代非线性电阻建立了一个四阶自治非线性电路,讨论了其中混沌演化过程并解释了由危机引起的间歇现象.

由于非光滑系统在分界面上会出现各种非常规分岔,尤其是多次穿越时可能会发生组合分岔,当非光滑系统存在不同的时间尺度时,这些相对比较特殊的非常规分岔,不仅可能影响系统沉寂态和激发态的形式,同时也可能使得沉寂态和激发态之间发生转换,从而导致具有特殊行为的簇发振荡.因此,深入探讨非光滑系统中的不同尺度效应,对于揭示非光滑和多尺度两种因素同时存在下系统的复杂性及其机理具有一定的理论意义.

本文重点关注非光滑系统中的不同尺度效应.基于蔡氏电路,建立了含分段线性非光滑因素的四阶广义蔡氏电路系统;同时,通过串联一个周期变化的交变电流源并适当选取参数,使得电流源的周期变化频率与系统的固有频率之间存在量级上的差距,导致系统存在快慢两不同两时间尺度的耦合.通过其相应的广义自治系统的平衡点及非光滑分界面上的分岔分析,结合转换相图,给出了两种典型的对称式Fold/Fold周期簇发和Fold/Hopf周期簇发现象,并揭示了两类簇发振荡的分岔机理.

2 数学模型

作为典型的第一类非光滑系统,含有分段线性特性二极管的蔡氏振子(图1)由于系统相对简单,同时具有丰富的动力学现象以及在实验室容易重现[16],一直是分析各种非线性特征的重要系统之一[17].基于各种广义的蔡氏振子模型,得到了许多有价值的研究结果[18].

图1 电路原理图

为深入分析非光滑系统中的不同尺度效应,在此引入周期变化的交变电流源VG(图1),其相应的动力学模型可以表示为[19]

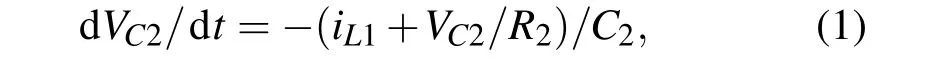
其中非线性电阻的伏安特性G(VC1)=P2VC1+(P1-P2)(|VC1+E0|-|VC1-E0|),周期变化电源特性VG=AGsin(ϖt),引入变化x=iL1/R1/E0,y=iL2R1/E0,u=VC1/E0,v=VC2/E0,t=,则(1)式可以表示为如下无量纲形式:

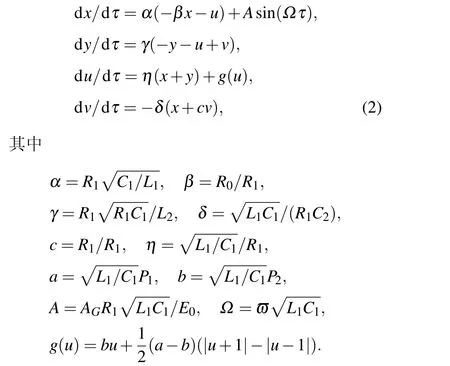
显然,四维非线性系统(2)式在u=±1处存在着非光滑特征,同时,当系统的固有频率与周期激励频率之间存在着量级差距时,会产生不同尺度效应,导致诸如大幅振荡和微幅振荡联合作用的多模态耦合振荡行为[20].为深入揭示其中的复杂动力学特性,探讨非光滑因素对其行为的影响,我们首先考察系统的各种分岔特性.

3 广义平衡点及其稳定性

簇发振荡过程中的沉寂态大都表现为围绕平衡态的微幅振荡,因此,从沉寂态到激发态的分岔行为基本上都是局部分岔,而周期激励下的非自治系统,通常表现为周期振荡,不会存在严格意义下的不动点.为分析其相应的沉寂态形式及其可能产生的分岔行为,进而揭示簇发振荡的机制,在此我们引入了广义平衡点的概念.

注意系统中的周期激励项w=Asin(Ωτ),设系统的固有频率为ω,当周期激励频率Ω≪ω时,则在每一固有频率的振动周期时间段Ψ内,w变化很小,也就是说,在系统每一固有频率振荡周期Ψ内,即τ∈[T0,T0+Ψ],其中T0为开始计时的起始点,w虽然在wA=AcosΩT0和wB=AcosΩ(T0+Ψ)之间变化,由于wA与wB非常接近,因此在每时间段Ψ内,w可以近似视为常数,系统的行为则主要由w取wA和wB之间的某一近似常数时相应的自治系统决定,而w的微小变化则起到调谐作用[21].因此在Ω≪ω时,虽然整体w会在[-A,A]之间变化,而在每一考察的相对较短时间范围内,w可以近似作为常数,此时周期激励下的非自治系统可以看作相应的自治系统,称为广义自治系统,其相应的平衡点则称为广义平衡点.

令系统(2)中周期激励项为w=Asin(Ωτ),A和Ω分别代表外激励的振幅和频率,则其相应的广义自治系统可以表示为

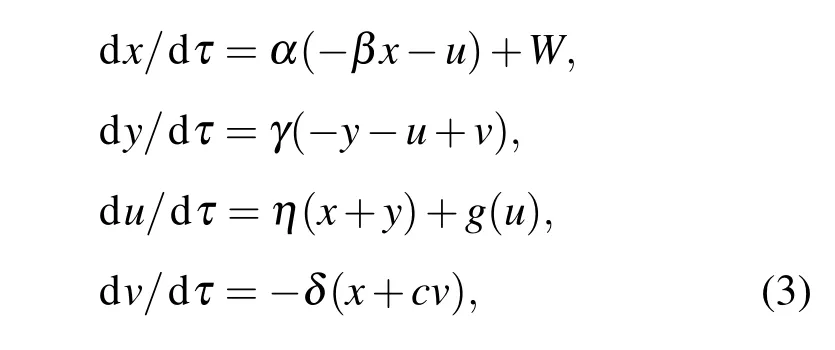
3.1 区域D0中的平衡点及其稳定性

在区域D0中,系统仅存在一个平衡点E0=(m1/M,m2/M,m3/M,m4/M),其 中 M= α(βacβc-c-1),m1=c(a-1)w,m2=(a+c)w,m3=-(c+1)w,m4=(a-1)w,其稳定性由其相应的特征多项式决定,表示为

因此,当参数满足条件 a1＞0,a1a2-a3＞0,a3(a1a2-a3)-＞0时,其相应的所有特征值均具有负实部,即平衡点E0为渐近稳定的.

3.2 区域D±中的平衡点及其稳定性

在两区域D±中,系统均存在着惟一的平衡点E±=(n1/N,n2/N,n3/N,n4/N),其中

由于对称性,其相应的特征多项式相同,统一表示为

因此,当参数满足条件 b1＞0,b1b2-b3＞0,b3(b1b2-b3)-＞ 0时,P±(λ)=0的所有解的实部均为负值,故E±是渐近稳定的.

4 广义自治系统的分岔分析

随着参数的变化,不同子区域中的平衡点会失去稳定性,产生不同的分岔行为,导致各种动力学特性.为此,首先考察各区域中平衡点失稳的分岔条件及其相应的分岔模式.

4.1 区域D0中的平衡点的分岔

由特征多项式(4)可知,平衡点E0存在两种失稳模式,也即当参数满足条件

时存在单零特征值,可能会导致平衡点产生跳跃现象;而当参数满足

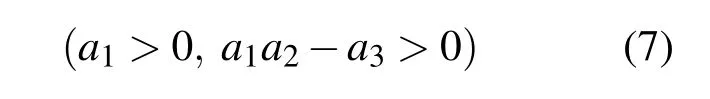
时存在一对纯虚根,可能产生Hopf分岔,导致周期振荡行为.

4.2 区域D±中的平衡点的分岔

由于对称性,D±中的平衡点具有相同的特征方程,因此也相应地存在着相同的失稳条件及其分岔模式.由(5)式可知,当参数满足

时存在单零特征值,可能会导致平衡点之间的跳跃现象;而当参数满足

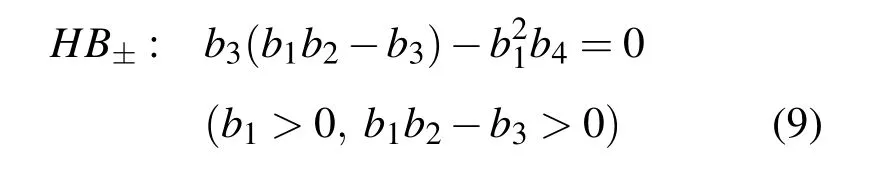
时存在一对纯虚根,可能产生Hopf分岔,导致系统产生周期振荡行为.

4.3 分界面上的非光滑分岔

下面着重分析系统在分界面Σ1,2处的分岔.考虑到系统(3)的向量场依然保持连续性,可以利用广义Clarke导数得到一个广义Jacobian矩阵,表示为

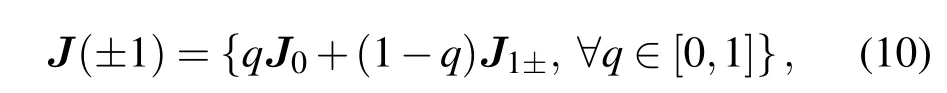
其中J0和J1分别表示分界面两边平衡点的特征矩阵,从而可得广义Jacobian矩阵的特征方程为

通过辅助参数q,分界面两边的Jacobian矩阵光滑连接.取定参数

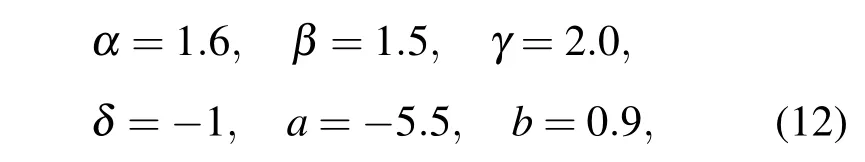
图2(a)和(b)分别给出了参数c=0.1和c=0.2时广义Jacobian矩阵J(±1)的特征值分布情况.

对于c=0.1,当q=0.9219,其特征曲线在复平面上穿越原点,其相应的广义Jacobian矩阵具有零特征值(图2(a)),说明当系统轨迹穿越非光滑分界面时,可能产生非常规Fold分岔.对于c=0.2,当q=0.0004时,其相应的广义Jacobian矩阵穿越纯虚轴,即产生了一对纯虚根,而当q=0.401时,其特征曲线又穿越原点,即产生零特征值.这说明,当辅助参数q从0变化到1,也即轨迹穿越非光滑分界面,其广义Jacobian矩阵会产生多次穿越分岔,该非常规分岔不仅具有Fold分岔的特征,同时也具有Hopf分岔的特征,也即非常规Fold/Hopf分岔.计算表明,此时与Hopf分岔相应的振荡频率为0.9210.

图2 随辅助参数变化的广义Jacobian矩阵特征曲线(a)c=0.1;(b)c=0.2

为描述非光滑分界面上的非常规分岔特性,下面结合分界面两边平衡点特性做示例说明.表1分别给出了参数c=0.1和c=0.2时,D0和D±区域中平衡点相应的特征值.对于c=0.1,注意到在D0区域中不同的焦点E0穿越分界面到D±中的稳定焦点E±时,其中的特征值从正变为负,即穿越零点,产生非常规Fold分岔.同样对于c=0.2,两边的平衡点不仅穿越零点,也要穿越虚轴,会产生Fold和Hopf的组合分岔,即非常规Fold/Hopf分岔.

表1 不同区域中平衡点的特征值及非光滑分岔

5 簇发振荡及其机理分析

当系统(2)中激励项的频率远小于系统的固有频率时,系统会产生簇发振荡现象,当参数如(12)式取定时,计算可知c=0.1的系统的固有频率为ω1=0.964,而在c=0.2时,其固有频率为ω2=0.921,此时取激励频率Ω=0.02,显然该频率与系统的固有频率之间存在着量级差距,因此会产生不同尺度耦合效应.图3分别给出了在激励幅值A=7.0下c=0.1和c=0.2时系统的相图及其相应的时间历程.

从图3可以看出,系统表现为关于原点对称的周期振荡,此时两个频率均参与系统的振荡行为,呈现出快变振荡与慢变振荡交替进行的典型快慢特征,也即周期簇发振荡.

5.1 转换相图

为进一步探讨其中的分岔机制,在此我们引入转换相图的概念.所谓转换相图,指的是将系统的相轨迹投影到非真实状态变量空间或平面中,如对于(3)式的周期激励系统,其轨迹可以表示为 (x,y,z)=(x1(τ),y1(τ),z1(τ)). 该轨迹可以在(x,y,z)三维空间或(x,y)等二维平面上投影,得到传统的相图,也可以向(x,w)或(y,w)等平面上投影,其中 w=Asin(Ωτ),其相应的平面轨迹为 (x,w)=[x1(τ),Asin(Ωτ)]或 (y,w)=[y1(τ),Asin(Ωτ)]. 由于 w=Asin(Ωτ) 不是真实的状态变量,此时称 (x,w)=[x1(τ),Asin(Ωτ)]或(y,w)=[y1(τ),Asin(Ωτ)]等为转换相图.

图3 簇发振荡的相图及时间历程图 (a)c=0.1;(b)c=0.2

5.2 对称的Fold/Fold簇发振荡

图4给出了c=0.1时系统在(u,x)和(u,y)平面上的相图,此时系统表现为典型的周期簇发振荡.结合图3中的空间结构及其相应的时间历程图可以看出,此时簇发振荡存在着两种不同的阶段,一是相对平缓的运动,对应于簇发过程的沉寂态(quiescent state),二是相对剧烈的大幅振荡,对应于激发态(spiking state).

图4 (a)u-x平面的相图;(b)u-y平面的相图

在簇发振荡过程中存在两种重要的分岔行为,也即从沉寂态到激发态的分岔以及从激发态到沉寂态的分岔.下面我们结合转换相图来分析两种不同状态之间的分岔连接过程.图5给出了(w,u)平面上相应的转换相图以及 dw/dτ与u之间的关系图.

5.3 簇发振荡机制

周期簇发振荡的轨迹穿越了两条分界面,注意到此时系统在不同区域的平衡点在广义相平面(w,u)形成倒Z形曲线(见图5(a)),其中在两分界面之间的中间部分为不稳定平衡点,而在区域D±中为稳定的焦点E±.以转换相图中的轨迹与非光滑分界面Σ1+的交点A1作为起点,由上节的分析知当辅助参数q=0.9219时,广义Jocabian具有零特征值,说明系统在穿越非光滑分界面Σ1+可能会产生Fold分岔,同时从图5(b)可以发现,在A1点dw/dτ＜0,因此轨迹在穿越Σ1+时由Fold分岔导致轨迹从A1点向倒Z形曲线的下半支也即稳定焦点E-跳跃.

图5 对称的Fold/Fold簇发机制 (a)w-u转换相图和对应自治系统平衡点分岔以及非光滑分界面叠加;(b)与u的关系

注意到在区域D0没有稳定的平衡点,所以轨迹会穿过D0区域.经计算,系统在区域D0中的不稳定平衡点所对应的四个特征值分别为λ1=0.0076,λ2,3=-3.9788±1.064i,λ4=-1.8500,由于λ1在数值上相对较小,因此轨线从点A1到点A2的过程比较慢,这也可以从相应的时间历程得到证实(见图3(a)).

当轨迹穿过区域D0到达A2点,也即非光滑分界面Σ1-上时,虽然轨迹穿越Σ1-也可能会产生非常规Fold分岔,但是该分岔并未发生.

从图5(b)可以发现,轨迹在A1和A2产生的区别的主要原因在于在A1和A2点处均满足dw/dτ＜0,也即轨迹在A1将通过分界面Σ1+进入区域D0,而在A2点将通过Σ1-进入区域D-,注意到区域D0中不存在稳定的平衡点,所以产生轨迹的跳跃现象,而在区域D-中,E-是稳定的,这就使得轨迹直接趋于稳定的E-,无法产生跳跃,导致潜在的Fold分岔没有发生.

相应地,由于轨迹在两非光滑分界面Σ1±之间穿过D0区域,不会产生剧烈的振荡行为,对应着簇发振荡中的沉寂态,说明从D+中的激发态通过A1点的Fold分岔进入在D0区域中的沉寂态.

轨迹从A2点开始,在区域D-中运动,在区域D-中的平衡点经计算分别为=-0.0172±0.9644i,=-1.6828±0.4605i,也即存在一对实部绝对值非常小而虚部是常规量的共轭复特征根,注意到A2与倒Z形曲线平衡曲线的下半支存在一定的距离,当轨迹从A2逐渐收敛到平衡曲线时,会产生按照固有频率且振荡幅值减小很慢的逼近平衡曲线的振荡过程,从而导致大幅振荡行为,对应于簇发过程中的激发态.

系统轨迹最终会在D-区域中逐渐收敛于平衡曲线,当轨迹到达 A3时 dw/dτ=0,随后dw/dτ＞0,导致广义状态变量w的增加;当轨迹到达Σ1-上的A4点时,发生与在A1相同的Fold分岔行为,只是此时轨迹通过区域D0经Σ1+上的A5点跳向区域D+中倒Z形曲线平衡曲线的上半支,并产生与D-区域中相同的振荡行为.当轨迹到达极点A6时 dw/dτ=0,使得 dw/dτ变为负值,曲线回到A1点,完成一个周期振荡过程.

w的变化过程其实也可以直接从其表达式中看出,注意到在w=Asin(Ωτ)中A=7.0,说明w的值会在[-7.0,+7.0]区域中做光滑变化,而在w变化的一个周期T=2π/Ω=100π内,其轨迹会经历两个沉寂态和两个激发态过程,不同过程之间均由Fold分岔连接,产生对称式的Fold/Fold簇发,考虑到对称性及平衡曲线上下支都是稳定的焦点,我们也称之为对称式焦/焦型Fold/Fold簇发.

5.4 对称的Fold/Hopf簇发振荡

当参数c=0.2时,系统的行为会发生变化,图6给出了空间轨迹(见图3(b))在(u,x)和(u,y)平面上的投影,可以看出,此时系统仍做周期振荡,但振荡模式与上述对称式焦-焦型Fold/Fold簇发的模式有所区别,主要体现在其激发态部分的极限环特征非常明显.

图6 (a)u-x平面的相图;(b)u-y平面的相图

5.5 簇发振荡机制

图7给出了(w,u)平面上相应的转换相图以及dw/dτ与u之间的关系.注意到在c=0.2时,广义自治系统存在稳定的极限环,该极限环的产生与w的取值有关.

假设系统轨迹仍从非光滑分界面Σ1+上的B1点出发,由于此时 dw/dτ＜0,系统轨迹必须穿过区域D0,而当辅助参数q=0.401时,广义Jocabian矩阵存在零特征值,与上述分析相同,此时系统在非光滑分界面Σ1-上的点B1处发生了Fold分岔,发生跳跃现象,受D-中稳定极限环的吸引,轨迹将穿过区域D0到达分界面Σ1-上的B2点,在区域D0轨线主要受平衡点E0的影响.经计算,轨线在区域D0所对应的特征值为λ1=0.1165,λ2,3=-3.9759±1.0621i,λ4=-1.8648,由于λ1相对较小,因此轨线从点B1到点B2的过程比较慢,形成沉寂态.系统从点B2开始,轨线进入区域D-.计算发现,随着w的变化,广义自治系统会产生超临界Hopf分岔,导致周期振荡,此时虽然所产生的极限环是稳定的,但由于w从本质上说不是系统参数,而是一周期函数,所以只会发生围绕该极限环的振荡.系统轨迹从B2开始在D-内运动,由于w的变化,产生Hopf分岔,导致大幅的周期振荡.当轨迹到达w=-7的极值点B3时,轨迹的振荡幅值将逐步减小,直到分界面Σ1-上的B4,完成这部分的激发振荡.由对称性,同样在B4会产生Fold分岔,使得轨迹穿过区域D0到达分界面Σ1+上的B5点,在区域D+内产生Hopf分岔,使得系统从沉寂态转向激发态,并与区域D-中的过程类似,轨迹最终回到B1点,完成一个周期的簇发振荡.

图7 对称的Fold/Hopf簇发机制 (a)w-u转换相图和对应自治系统平衡点分岔以及非光滑分界面叠加;(b)与u的关系

在该簇发振荡过程中,Fold分岔使得系统从激发态进入沉寂态,而Hopf分岔导致系统从沉寂态回到激发态,同样簇发振荡具有对称性.而与上述对称式焦/焦型Fold/Fold簇发在不同焦点之间转换不同,该簇发是在焦点和极限环之间转换,因此我们称之为对称式点/环型Fold/Hopf簇发.

6 结论

对于具有两非光滑分界面的周期激励下的广义蔡氏电路,当激励频率与系统的固有频率之间存在量级差距时,会产生快慢效应,导致簇发振荡.通过广义自治系统的平衡点及其稳定性,近似分析了其中诸如Fold和Hopf等不同分岔行为及其产生条件,进而探讨了各种参数下系统的振荡特征,分析了不同沉寂态和激发态的产生原因及其相应的分岔行为,得到了对称式焦/焦型Fold/Fold型和对称式的点/环Fold/Hopf型两种簇发振荡,并结合转换相图,考察了两种簇发振荡的特点,揭示了不同簇发相应的产生机理.

[1]Shooshtari A,Pasha Zanoosi A 2010 Appl.Math.Model.341918

[2]Haselbacher A,Najjar F M,Massa L,Moser R D 2010 J.Comput.Phys.229325

[3]Merkin J H,Taylor A F 2012 Physica D 2411336

[4]Ernesto P,Dulce M,Soledad M,Jose M G,Santiago L,Julian J G 2006 Neurosci.Lett.394152

[5]Jia Z D,Leimkuhler B 2003 Future Generation Comput.Syst.19415

[6]Knoll D A,Chacon L,Margolin L,Mousseau V 2003 J.Comput.Phys.185583

[7]Rinberg A,Taylor A L,Mdarder E 2013 Plos Computat.Biol.9 e1002857

[8]Strizhak P E,Kawczynski A L 1995 J.Phys.Chem.9910830

[9]Ji Y,Bi Q S 2010 Phys.Lett.A 3741434

[10]Izhikevich E M 2000 Int.J.Bifur.Chaos 101171

[11]Chua L O,Lin G N 1990 IEEE Trans.Circ.Syst.37885

[12]Zhai D Q,Liu C X,Liu Y,Xu Z 2010 Acta Phys.Sin.59816(in Chinese)[翟笃庆,刘崇新,刘尧,许喆2010物理学报59816]

[13]Chen Z Y,Zhang X F,Bi Q S 2008 Nonlin.Anal.:Real World Appl.91158

[14]Stouboulos I N,Miliou A N,Valaristos A P 2007 Chaos Solition.Fract.331256

[15]Koliopanos C L,Kyprianidis I M,Stouboulos I N 2003 Chaos Solition.Fract.16173

[16]Yang Z M,Zhang J,Ma Y J,Bai Y L,Ma S Q 2010 Acta Phys.Sin.593007(in Chinese)[杨志民,张洁,马永杰,摆玉龙,马胜前2010物理学报593007]

[17]Binazadeh T,Shafiei M H 2013 Commun.Nonlinear Sci.Numer.Simulat.181071

[18]Ji Y,Bi Q S 2012 Acta Phys.Sin.61010202(in Chinese)[季颖,毕勤胜2012物理学报61010202]

[19]Zhang Y,Bi Q S 2011 Chin.Phys.B 20010504-1

[20]Li X H,Bi Q S 2012 Acta Phys.Sin.61020504(in Chinese)[李向红,毕勤胜2012物理学报61020504]

[21]Zhang Z D,Li Y Y,Bi Q S 2013 Phys.Lett.A 377975