孙艳红

(内蒙古民族大学数学学院，内蒙古通辽028000)

1 问题背景

设M是一个紧致、可定向的三维流形.F是真嵌入在M中的分离的并且没有环面分支的曲面.F的圆片复形记为Γ(F)，定义如下:

1)F的压缩圆片的合痕类构成Γ(F)的顶点集.

2)如果存在m+1个顶点的代表元彼此不交，则它们构成一个m维单形.

称曲面F是一个拓扑极小曲面，如果Γ(F)为空集，或者Γ(F)是不可缩的.并且称拓扑极小曲面F的拓扑指数(简称指数)为满足πn－1(Γ)≠1的最小的n.特别地，如果Γ(F)为空集，则定义为拓扑极小曲面F的指数为0.指数为0的拓扑极小曲面通常称为不可压缩曲面，这是三维流形理论中被广泛研究的一类重要曲面.指数为1的拓扑极小曲面称为强不可约曲面，这类曲面在三维流形理论中同样十分重要.拓扑极小曲面是由David Bachman［2］首次提出的，是近年来三维流形理论一个热门问题.它与微分几何中的极小曲面的概念有非常紧密的联系［2－3］.

拓扑极小曲面具有很多相似的性质，即使拓扑指数可能并不相同.例如，三维流形中嵌入的不可压缩曲面和任意指数的拓扑极小曲面，都可以合痕移动使得交线在两个曲面上都是本质的.

对于一般情况，David Bachman对指数≥2的拓扑极小曲面做了深入研究，首先证明了任意指数的拓扑极小曲面是存在的［3］.特别地，David Bachman引入了临界曲面(critical surface)的定义［1］，并证明了临界曲面是指数为2的拓扑极小曲面.因此给出了指数为2的拓扑极小曲面的等价定义.

定义1［3］F是M中的一个临界曲面(critical surface)，如果F的压缩圆片的合痕类可以分解成两个不交的非空子集C0和C1如下:

1)对每个i=0，1，存在 F 的两个压缩圆片 Di，Ei∈Ci，Di，Ei位于 F 的不同侧并且交集为空;

2)对任意两个压缩圆片满足V∈C0，W∈C1，并且V与W位于F的不同侧，则V与W的交集不为空.

尽管这个定义更加直观，然而目前已经知道的临界曲面的例子仍然非常少.Lee Jung Hoon在文献［6］中给出了一种利用“边界稳定化”构造临界Heegaard曲面的方法.本文在Lee Jung Hoon工作的基础上，证明了边界稳定化后的Heegaard曲面是临界曲面时，原来的Heegaard曲面具有不交线性质.

2 预备知识

本节首先介绍一些三维流形理论中的预备知识.设M是一个紧致连通可定向的三维流形.则M可以看成两个压缩体V和W，沿着它们同胚的正边界，通过一个保持定向的同胚映射粘合得到的.称这样的分解为M的一个Heegaard分解，记为M=V∪HW，其中∂+V=∂+W=H称为M的Heegaard曲面.

称M=V∪HW是弱可约的，如果存在V中本质的圆片D和W中本质的圆片E，使得D和E在H上不交.否则，称M=V∪HW是强不可约的.有关强不可约和弱可约Heegaard分解的性质，可以参考文献［4］.

当M是一个带边流形时，每一个边界分支必属于V或W的负边界集合.M=V∪HW是一个Heegaard分解，S⊂∂M，不妨设 S⊂∂－W.则可以构造 M 的另一个 Heegaard 分解 M=V*∪H*W*，使得∂－V*=∂－V∪S，∂－W*=∂－WS，构造方法如下:在压缩体 W 中，考虑 S的一个正则邻域 S×I，记S=S×(0)，在 W(S×I)(实际上它同胚于W)中取一条简单弧α，使得顶点分别在∂+W和S×(1)上，并且假设它与W中的 1－把柄不交.令 V*=V∪N(α)∪(S×I)，W*=MV*=W((S×I)∪η(α))，H*=V*∩W*.容易验证M=V*∪H*W*.称M=V*∪H*W*为M=V∪HW关于曲面S的边界稳定化.容易验证g(H*)=g(H)+g(S)，其中g(F)表示曲面F的亏格.

设M是一个三维流形，V∪HW是M的一个强不可约的Heegaard分解.如果存在V中的一个本质圆片D，W中的一个本质圆片E，以及H上的一条简单本质闭曲线α，使得α与D，W的边界都不交.则称V∪HW具有不交线性质.关于具有不交线性质的Heegaard分解的研究已经取得很多成果.实际上不交线性质也可以用Heegaard距离等于2来描述，不在这里叙述Heegaard距离，感兴趣的读者可以参考文献［5］.

不交线性质的一个特殊情况是不交(D，A)性质:我们称压缩体中的一个本质平环为扩展平环，如果它的两个边界分别在压缩体的正、负边界上.设M是一个三维流形，V∪HW是M的一个强不可约的Heegaard分解.如果存在V中的一个本质圆片D，和W中的一个扩展平环A使得D∩A=∅，则称V∪HW具有不交(D，A)性质.容易证明，具有不交(D，A)性质的Heegaard分解一定具有不交线性质.

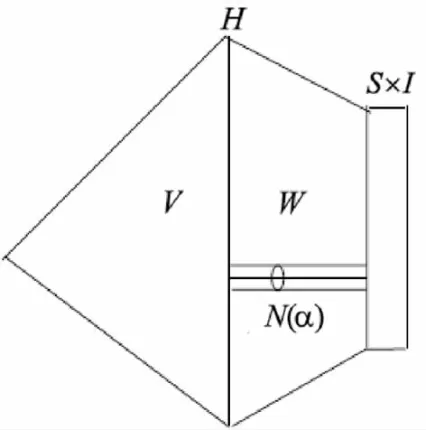
图1 边界稳定化Fig.1 Boundary stabilization

注记1 本文中提到的不交线性质和不交(D，A)性质，都是假设V∪HW是强不可约的.容易证明，如果Heegaard分解V∪HW是弱可约的，则V∪HW一定具有不交线性质，本文不考虑这种情况.

3 主要结果

首先介绍Lee Jung Hoon在文献［6］中的一个结果.它给出了边界稳定化后的Heegaard曲面是临界曲面的一个充分条件.为了方便读者以及后文需要，我们同时给出这个定理的完整证明.

定理1［6］设M是一个紧致连通并且可定向的三维流形，S=∂M是连通的曲面，V∪HW是M的一个强不可约的Heegaard分解，S=∂－W，M=V*∪H*W*为M=V∪HW关于曲面S的边界稳定化.则当V∪HW具有不交(D，A)性质时，H*是M的一个临界Heegaard曲面.

证明 在A中选取一条本质的弧 α，令V*=V∪N(α)∪(S×I)，W*=MV*=W(S×I)η(α)，H*=V*∩W*，M=V*∪H*W*是V∪HW关于曲面S的边界稳定化.记V*中的1－把柄N(α)对应的压缩圆片为B.对H*的压缩圆盘集的合痕类做一个分划C0和C1，并按照属于V*或W*进一步分划成如下四个集合:

1)C0∩V*为压缩圆片B;

2)C0∩W*为与B不交的圆片集;

3)C1∩V*为与B不合痕的圆片集;

4)C1∩W*为与B相交的圆片集.

显然，H*的压缩圆盘集的每一个元素一定属于并只属于上述四个集合之一.我们需要证明这个分划满足定义1中临界性.

首先，证明C0和C1满足定义1中的条件(1).W中的本质原片仍然是W*中的本质圆片，它与B不交，因此属于C0∩W*，因此C0中存在两个位于H*异侧的不交圆片.另一方面，D是V的本质圆片，同样也是V*中的本质圆片，它与B在V*中不合痕，因此属于C1∩V*，A－N(α)是W*中的本质圆片，由于它与B相交于2个点，它属于C1∩W*.由假设，D与A不交，因此D与A－N(α)不交.故C1中也存在两个位于H*异侧的不交圆片.

其次，证明C0和C1满足定义1中的条件(2).首先，C0∩V*的圆片与C1∩W*的圆片相交是显然的，因此，我们只需证明C0∩W*中的圆片与C1∩V*中的圆片相交.任取C0∩W*中的一个圆片E，由于它与B不交，因此E可以合痕与N(α)不交.故E可以看成是W中的本质圆片.任取C1∩V*中的一个圆片F，我们用反证法证明E与F一定相交，从而完成证明.假设E与F不交.由于F与B不合痕，我们假设选取的F，是C1∩V*与B相交数最小，并且与E不交的圆片.如果F∩B为空集，则F是V中的本质圆片，由于V∪HW是强不可约的，故E∩F不为空集，这与我们的假设矛盾.因此F∩B不为空集，由最小交线假设，以及标准的最内圆片讨论和标准的最外弧讨论，F∩B是一些弧集合，并且在F上界定的最外子圆片在V*中是本质的，由于B将V*切成V和S×I，而S×I中是不存在本质圆片的，故在F上的最外弧在F上界定的最外子圆片是在V中是本质的，记为Δ.再一次由V∪HW是强不可约性，可以知道E与Δ是不交的，然而E与Δ的交点同样也是E与F的交点，这与我们假定E与F不交是矛盾的.因此假设不成立，E与F一定是相交的.

证明了C0和C1满足临界性的定义，因此H*是M的一个临界Heegaard曲面.下面给出边界稳定化后的Heegaard曲面是临界曲面的一个必要条件.

定理2 设M是一个紧致连通并且可定向的三维流形，S=∂M是连通的曲面，V∪HW是M的一个强不可约的Heegaard分解，S=∂－M.M=V*∪H*W*为M=V∪HW关于曲面S的边界稳定化.若H*是M的一个临界Heegaard曲面，则V∪HW具有不交线性质.

证明 假设M=V*∪H*W*为强不可约的Heegaard分解M=V∪HW关于曲面S的边界稳定化.H*是M的一个临界Heegaard曲面.因此，存在H*的压缩圆片的一个分划，记为C0和C1，满足定义1中的两个条件.

同样记V*中的1－把柄N(α)对应的压缩圆片为B.不妨假设B属于C0的，即属于C0∩V*.显然C1∩V*中的圆片在V*都不能合痕于B，由临界曲面的定义，C1∩W*中的圆片一定与B是相交的.并且存在C1∩V*中的一个圆片D*，C1∩W*中的一个圆片E*，使得D*与E*不交.

由于D*是V*中与B不合痕的圆片，并且B将V*切成V和S×I，而S×I中不存在不可压缩的带边曲面，因此D*可以合痕移动使得与B不交，并且完全落在V中.因此D*实际上是V中的本质圆片.

考虑曲面H－N(α)，它是H的子曲面，记为H1，H1带有一个边界曲线记为t，∂E*∩H1是一些弧.由于E*是本质的，至少一条弧在H1上是本质的，记为l.l的顶点落在t上，并把t分解成t1和t2.l∪t1或者l∪t2是H*上一条简单的本质的闭曲线.

由于D*与E*不交，因此D*与l∪t1(或者l∪t2)是不交的.由于M=V∪HW是强不可约的，l∪t1在W中不能界定圆片，否则M=V∪HW就是弱可约的.最后证明W中一定存在本质圆片，使得∂J与l∪t1不交.任取W中一本质圆片J，使得它是所有本质圆片中与E*的交集为最小的，显然J也可以看成是W*中的本质圆片.由标准的最内圆片讨论可知，J与E*交线是弧分支，再由标准的最外弧讨论可知，如果存在弧分支，可以通过标准的切割与粘贴的方法找到一个W中一本质圆片J＇，使得，这与假设J与E*的交集为最小矛盾，因此J与E*是不交的.所以J与l∪t1也是不交的.

因此l∪t1是H上本质的简单闭曲线，它与V中的本质圆片D不交，与W中的本质圆片J不交，所以V∪HW具有不交线性质.

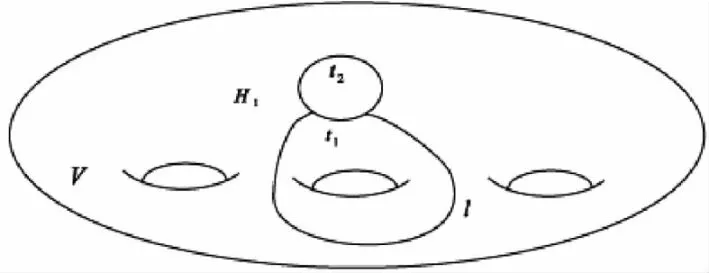
图2 H1上的本质弧Fig.2 Essential arcs in H1

4 结论与展望

设M是一个紧致连通并且可定向的三维流形，S=∂M是连通的曲面，M=V∪HW是M的一个强不可约的Heegaard分解，S=∂－W.M=V*∪H*W*为M=V∪HW关于曲面S的边界稳定化.H*是M的一个临界Heegaard曲面的充分条件是V∪HW具有不交(D，A)性质，必要条件是V∪HW具有不交线性质.

希望进一步得到这个问题的充分必要条件，具有不交线性质但是不具有不交(D，A)性质的Heegaard分解，边界稳定化后的Heegaard曲面是否一定为临界曲面?这个问题有待研究.

［1］ Bachman D.Critical Heegaard surfaces［J］.Trans Amer Math Soc，2002，354:4015－4042.

［2］ Bachman D.Topological index theory for surfaces in 3－manifolds［J］.Geom Topol，2010，14:585－609.

［3］ Bachman D，Johnson J.On the existence of high index topologically minimal surfaces［J］.Math Res Lett，2010，17:389－394.

［4］ Casson A J，McA Gordon C.Reducing Heegaard splittings［J］.Topology Appl，1987，27:275－283.

［5］ Hempel J.3－manifolds as viewed from the curve complex［J］.Topology，2001，40:631－657.

［6］ Lee J H.Critical Heegaard surfaces obtained by amalgamation［J］.Topology Appl，2013，160(1):111－116.