陈宁华

(福建幼儿师范高等专科学院，福州福建350007)

文献［1］中讨论了具有连续征时滞和离散时滞的非线性系统:

的周期解的存在性和唯一性问题，这里 t∈R，x∈Rn;A(t，x)，C(t，s)为 n×n 连续的函数矩阵;gj(t，x)(j=1，2，…，m)，b(t)是n维连续向量.

本文将考虑系统n很大时，即式(1)为大系统的情况.设x(t)=(x(1)(t)，x(2)(t)，…，x(l)(t)T，x(i)(t)∈其中 A ij(t，x(t))为 nij的函数矩阵，i，j=1，2，…，l;gj(t，x)=1，2，…，l;C(t，s)=(Ci，j(t，s))n×n，其中 Ci，j(t，s)为 ni×nj的函数矩阵，i，j=1，2，…，l，gj(t，x)=(g(j1)(t，x)，(g(j2)(t，x)，…，g(jl)(t，x))T，b(t)=(b(1)(t)，b(2)(t)，…，b(l)(t))T，其中 g(ji)(t，x)∈Rni，b(i)(t)∈Rni，且同时假设 A(t，x)，C(t，s)，gi(t，x)，b(t)分别在 R×Rn，R×R，R×Rn，R 上连续，而且存在 T＞0，使得 A(t+T，x)=A(t，x)，C(t+T，s+T)=C(t，s)，gj(t+T，x)=gj(t，x)，τj(t+T)= τj(t)，b(t+T)=b(t)，j=1，2，…，l.

系统(1)等价于:

(A1)设存在正的连续可微的T－周期函数d(i)h(t)，h=1，2，…，ni和连续的T－周期函数 α(i)1(t)满足:

(A3)有界，且 ∀ε ＞ 0，存在 L=L(ε)＞ 0，使得对任意的 t1＞-∞，t-t1≥ L，有

(A4)存在非负连续的T－周期函数G(i)j(t)，使得:

(A5)存在常数，使得∀t∈R，有

2 引理

考虑周期系统:

和

其中A(t)=(aij(t))n×n是R上n×n的连续函数矩阵，f(t)是R上的n维连续函数向量且A(t)，f(t)关于t是T－周期的.

(H1)存在正的连续可微的T－周期函数di(t)(i=1，2，…，n)和连续的T－周期函数α3(t)满足:

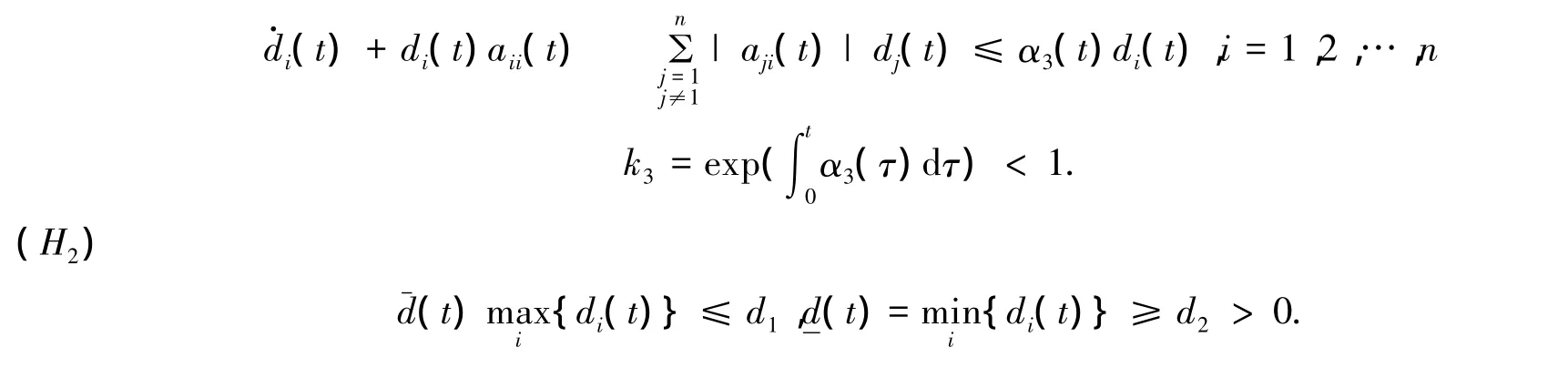
(H3)有界;(ii)对于任意的ε＞0，存在L=L(ε)＞0，使得对任意的t1＞-∞，tt1≥ L，有

引理1［2］设 X(t)是方程(3)的基本解矩阵，若 A(t)满足(H1)和(H2)，则有

引理2［1］若T-周期函数α3(t)满足，则有:

引理3［2］设λ(t)是连续的T-周期函数，则

引理4［2］对于方程(4)，若A(t)满足(H1)和(H2)，则方程(2)存在唯一的T－周期解:

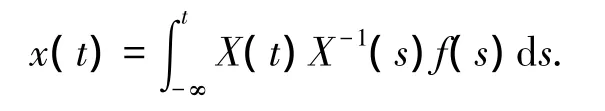
引理5［3－8］设C(t，s)为n×m连续T－周期函数矩阵且满足(H3)，如果f1(t)是m维连续的T－周期函数，则g(t)也是连续的T－周期函数.

考虑如下的微分系统:

其中 t∈R，x∈Rn;(A(t))n×n，(C(t，s))n×m都是连续 T－周期函数矩阵;f1(t)，f2(t)分别是 m 维、n 维的连续 T－周期函数.利用上述引理，得:

引理6［1］设C(t，s)为n×m连续T-周期函数矩阵且满足(H3)，A(t)满足(H1)和(H2)，则方程(5)存在唯一的T-周期，其中X(t)为方程(3)的基本解矩阵.

3 主要结论

定理1 如果满足条件(A1)～(A5)，则大系统(1)至少存在一个T－周期解.

证明 设B={u(t)|u(t)=(u(1)(t)，u(2)(t)，…，u(l)(t)):R→Rn连续 T－周期函数}，则 B是在范数下的一个Banach空间.对任意的u∈B，考虑方程:

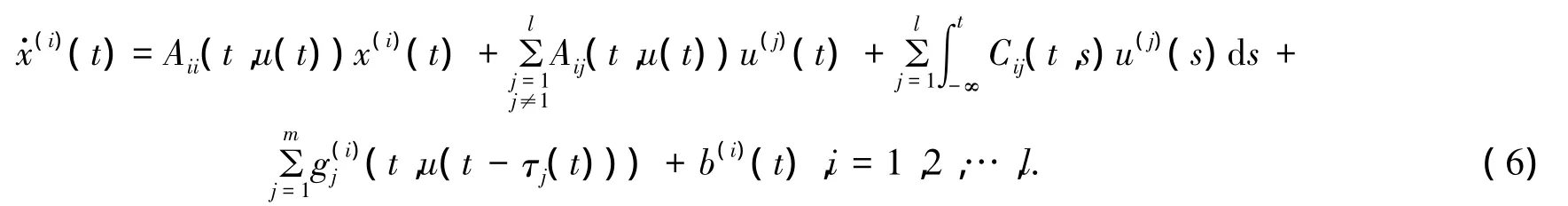
对任意的 u∈B，定义映射 F:B→B，Fu(t)=xu(t)，这里 xu(t)=(x(1)u(t)，x(2)u(t)，…，x(l)u(t)T，F=(F(1)，F(2)，…，F(l))T，Fu(t)=(F(1)u(t)，F(2)u(t)，…，F(l)u(t))T，其中 F(i)u(t)=x(i)u(t).

下面用Schaudar不动点定理证明F在B中至少有一个不动点.为此，记，其中n为自然数.

1)先证明存在自然数 N，使得 F:Dn→DN.若不然，对任意的自然数 n，都存在 i∈{1，2，…，l}和 un∈Dn，使得

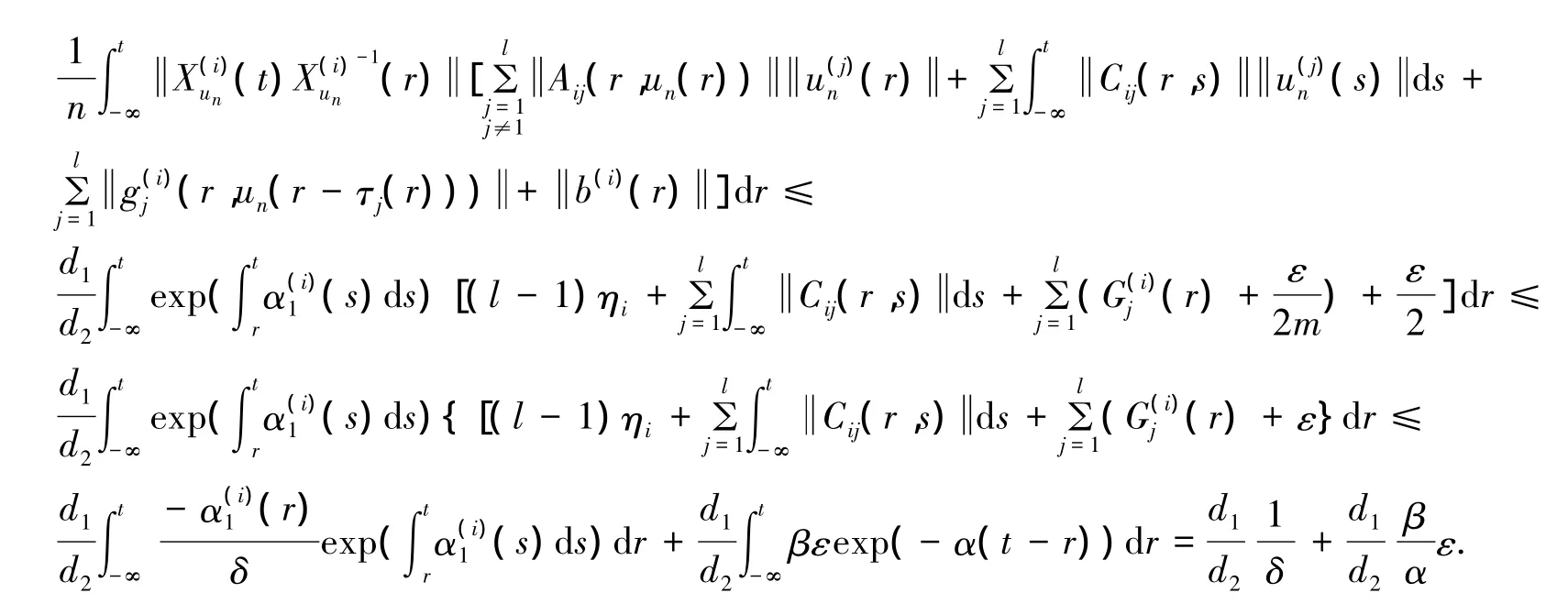
2)证明FDN是B中的紧子集.事实上，因为FDN⊆DN，所以{Fu(t)|u∈DN}是一致有界的.记x)∈［0，T］× RN，这里又因为对任意的u∈DN，有:

3)证明F在DN上连续的，即证F(i)在DN上连续.因为g(i)j(t，x)在［0，T］×RN上一致连续且关于t是T－周期的，故 g(i)j(t，x)在 R×RN上一致连续，从而对于任意的 ε＞0，存在 δ(i)j＞0，当时，有.对上述的 ε＞0，取，由定理的条件可得，对任意的 u1，u2∈DN，t∈R，只要，就有:

综上可知，F:DN→DN是全连续算子，故由Schauder不动点定理知F在DN上至少有一个不动点，即T－周期解.

［1］ 陈凤德，孙德献，史金麟.一类积分微分方程周期解的存在性和唯一性［J］.数学学报，2004，47(5):973－984.

［2］ Zhou Z F.Periodic Solution for a class of higher dimensional retarded functional differential equations［J］.J of Math(PRC)，2002，22(4):423－430.

［3］ Wang Q Y.Existence，uniquesness and stability of periodic solution of integrodifferenial equations with infinite delay［J］.Acta Mathematics Applications Scinica，1998，21:312－318.

［4］ 何崇佑.概周期微分方程［M］.北京:高等教育出版社，1992.

［5］ 林木仁.某类大系统有界解的存在性［J］.福州大学学报:自然科学版，2003，31(1):1－5.

［6］ Yuan Rong.Stability and existence of periodic solution and almost solution of large system［J］.Ann of Diff Eqs，1990，6(1):21－30.

［7］ Xu J Y.Global exponential p－stability in Colen－Grossberg－Type bidirrectional associative memory neural networks with transmission delays and learning behavior［J］.J Appl Math and Comput，2010，32:519－534.

［8］ Xu J Y，Chen L J，Li Z.Convergence behavior of delayed bidirectional associative memory cellular neural networks with asymptotically periodic coecients［J］.Appl Math Comput，2009，215:928－935.