邓伟胤 朱瑞 邓文基

(华南理工大学物理系,广州 510641)

(2012年10月16日收到;2012年11月17日收到修改稿)

1 引言

2004年,二维的石墨烯在实验上成功制备[1],引起广大科学工作者的强烈关注和研究[2].石墨烯独特的复式六角晶格结构使得在低能态下描述其状态的是Dirac方程,并且方程中的速度不是光速,而是光速的三百分之一[3],远低于光速,因此实验上容易实现和测量,这使得石墨烯可以成为检验量子电动力学理论的实验平台[4-6],从而为验证相对论量子力学理论由于高能量而难以实验提供了一条可行的路径.通过机械剥离[1,7]、表面外延生长[8]、印章挤压[9]、化学剥离[10]等方法可以制造出具有边界的有限尺寸石墨烯.由于石墨烯的实际样品总是有边界,因此为了对应实验和理论的工作,人们对作为一个简化的模型——石墨烯纳米带(GNRs)进行了研究.最常见的石墨烯纳米带有Zigzag型石墨烯纳米带(ZGNRs)和Armchair型石墨烯纳米带(AGNRs).在紧束缚近似下,Klein[11]最先开始研究了一系列不同宽度的纳米带;Son等[12,13]对GNRs的能带和能隙进行了研究,发现GNRs存在与纳米带宽度和边界形状有关的带隙;Sasaki等[14,15]推导了ZGNRs和AGNRs的电子态的解析表达式,结果表明ZGNRs的电子态有两类,分别是驻波态和边缘态.尽管人们对ZGNRs做了相当深入的研究,但是还有一些基本的物理性质没有弄清楚,例如电子态从驻波态到边缘态的转变,还有边缘态的精确能带范围等.

多年来,如何求解有限尺寸晶体的电子态一直都是固体物理学的基本问题[16].在传统的固体物理学中,研究的是无限大的晶体,我们可以应用Bloch定理直接得到晶体的电子态形式.但是有限尺寸的晶体破坏了周期性,其晶格势不再具有平移对称性,因此Bloch定理不再适用.Ren[16-19]扩展了Bloch定理的理论,提出适合有限尺寸晶体的Bloch波的量子限域理论,并且在一维有限晶体中通过微分方程严格论证了解的形式和性质;值得注意的是,该理论是关于连续模型的晶体,并且在高维下还没有严格地证明[16].Zhang等[20,21]通过数值计算得到和Ren理论对应的一维晶体的电子态,Ajoy和Karmalkar[22]通过数值计算讨论其高维下电子态理论的合理性及适用条件.在这些基础上,我们提出有限系统的Bloch定理方法,来解析计算紧束缚近似下的有限石墨烯格点模型的电子态.我们认为这个方法是普适的,这将为其他有限尺寸晶体的电子态计算提供重要的参考.

在本文中,基于ZGNRs的紧束缚格点模型,首先在无限长方向应用Bloch定律,把它转化为对一个超原胞的求解,继而把超原胞化成二聚化原子链模型;在这基础上,利用有限系统的Bloch定理方法,解析地求解ZGNRs的电子态和能带.然后分析其电子态和能带的性质.结果表明其电子态有两类,分别是驻波态和边缘态.驻波态中,其波矢为实数,波函数是正弦函数形式;边缘态时,其波矢主要是虚数,实数部分为零或者π/2,波函数是双曲正弦函数形式.其能带由驻波态能量和边缘态能量组成.我们推导了驻波态的最大允许的能带范围,还有边缘态的关于无限长方向波矢的精确取值范围和能量的精确取值范围.最后详细讨论边缘态和驻波态的过渡点,发现两种电子态通过不同的方式在受限波矢趋于零时关于格点位置逼近线性关系.本文的主要目的是利用有限系统的Bloch定理方法解析地求解ZGNRs的电子态和能带,通过分析其中的量子过渡点和边缘态能带的精确范围,以给出一个关于理想的ZGNRs更清晰和更准确的物理图像.在这之后,我们可以在后续的工作中考虑存在边界弛豫[12]和次近邻跃迁作用[14,23]时的电子态和能带,以更接近实际的石墨烯纳米带.

2 模型与方法

2.1 模型与二聚化原子链

ZGNRs结构如图1(a)所示,x方向是有限尺寸,边界形状是Zigzag型;y方向是无限长.选择虚框部分为超原胞,一共包含2N个原子,其中N个A原子,用绿色表示;N个B原子,用红色表示.在紧束缚近似下,容易得到格点的本征方程

其中φi表示位于格点i处的波函数,εi是相应的座能量,ti,i+δ表示电子由格点i到最近邻格点i+δ的跃迁能,δ表示最近邻.由于y方向是无限长的,满足平移不变性要求,由Bloch定理可知超原胞外的格点本征方程总是可以平移到超原胞内,它们的波函数只是一个相位的不同,概率密度是一样的,因此我们只需研究超原胞内格点的本征值和波函数,就可推广至整个石墨烯纳米带.对于超原胞内的格点,从左边界往右,一个周期单元有A(i+1,j)/B(i+2,j)/A(i+3,j)/B(i+4,j)四个格点,只有四个格点的本征方程具有不同的形式.根据(1)式,它们的本征方程分别为

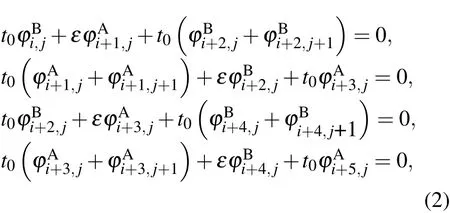
其中 i=4n,(n=0,1,2,···);φA,φB分别表示 A格点和B格点的波函数;-t0为最近邻跃迁能,t0=2.7 eV;ε=E-εi,E是本征能量,我们选座能量为能量零点,即εi=0,所以ε=E.利用Bloch定理,即超原胞的独立本征方程可化成

图1 ZGNRs的理论模型 (a)ZGNRs结构图;(b)二聚化原子链模型图

值得注意的是,(3)式方程正是如图1(b)所示的二聚化原子链上的紧束缚电子态方程;也就是说,在进行波函数相位变换后,我们把ZGNRs的超原胞模型转化成有限的二聚化原子链模型.

2.2 有限系统的Bloch定理方法

研究有限系统的能带和波函数,可以用Bloch定理得到尝试波函数,然后通过能带的简并关系,求出其中满足边界关系的波函数,进而确定本征值的取值,我们称这种方法为有限系统的Bloch定理方法.对于二聚化原子链,由Bloch定理可设能量本征态的尝试波函数为

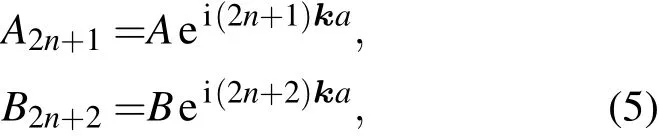
由Cramer法则得定解条件为

其中ka≡β+iα,它的允许取值分成两大类,即或者波矢为实数,即α=0;或者β=0,π/2,波矢具有非零的虚部,α待定.

如果超原胞是无限长的,即石墨烯是二维无限大时,有2ka=xa0/2,连续取实数值,能带为

这正是无限大石墨烯的能带[24].

3 结果与讨论

3.1 驻波态

在第一种情况下,波矢为实数,α=0.解得正负两支能带

对应的波函数分别为

其中

且φ(-k)=-φ(k),相位是奇函数关系,波矢ka∈(-π/2,π/2).

对于有限长原子链,还需要选择特殊的波矢量k保证波函数的边条件(4)式得到满足.注意到色散关系为偶函数,即ε(-k)=ε(k),我们尝试将波矢为k和-k的两个行波能量简并态叠加为一个驻波,即

其中 n=0,1,2,···,N.边条件 (4)成为

(12)式中的波函数最后整理为

其中归一化常数待定.由(13)式可得

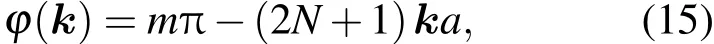
其中m为依赖于波矢k的整数.所以波函数还可以进一步整理为

参数m决定波函数的宇称.归一化系数为

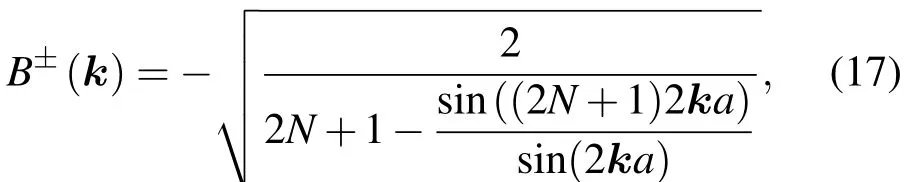
归一化系数与波矢量k有关,我们取负的归一化系数,是为了在以下研究电子态过渡性质时更加简单.波矢量由(11)和(15)式确定,这意味着波矢必须满足

因此,受限方向波矢k也与无限长方向波矢ky有关;要注意的是此时波矢ka∈(0,π/2),线性组合后新的波函数的波矢范围缩小到一半,受限波矢与无限长方向波矢有关.

若t=t0,二聚化原子链变成简单原子链.定解条件简化为

波矢的可能取值为

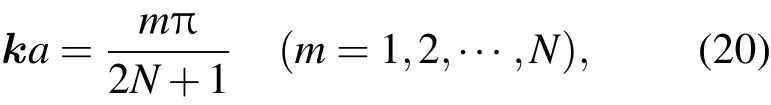
能量

波函数为

不难验算这正是一维简单原子链的电子态和能带的表达式,这验证了我们方法的可行性.

3.2 边缘态

若β=0,ka=iα.可解得正负两支能带

它们对应的波函数分别为

其中

同样地,需要选择特殊的虚波矢α保证波函数的边条件(4)得到满足.利用偶函数的色散关系ε(-α)=ε(α),将波矢为α和-α的两个能量简并态叠加,即

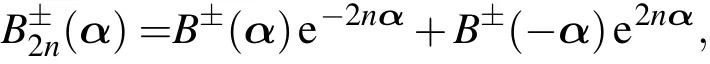
其中 n=0,1,2,···,N.边条件 (4)成为

(25)式中的波函数最后整理为

归一化系数

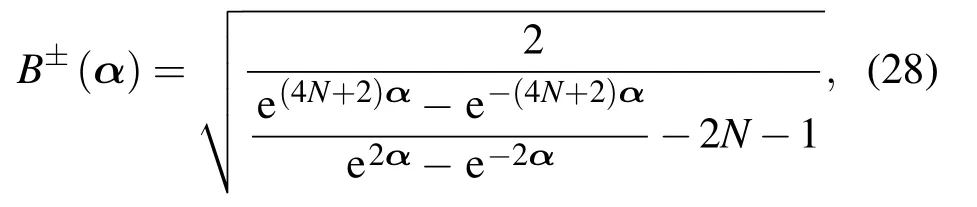
从中可以看出

归一化系数与波矢量α有关,由(26)式可得(2N+1)α+φ(α)=0,结合(24)式整理有

同理地,若β=π/2,ka=iα时,可以算出能带

波函数

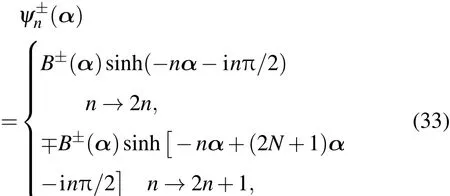
其中B±(α)与(29)式一样.波矢量满足的关系

受限的虚波矢与无限长方向波矢有关.

边缘态的概率密度图像如图2所示,其图像可由波函数(27)或(33)式描述.当能量E确定时,波矢量α也随之确定,可以看到概率密度随格点位置n是类指数函数的形式,边缘态是两重简并的,图中两条曲线分别是左边缘态和右边缘态,而不是只在其中一端边界出现.从图2(a)和2(b)中可以看到,随着能量趋于零,边缘态的局域性增大,这由以上对波矢量α的分析可知是因为能量趋于零时α不断变大所致.

图2 边缘态的概率密度 (a)E=3.78 meV;(b)E=5.94×10-8meV;N是原胞数,超原胞一共含2N个格点,ky的单位波矢为π/a0,E的单位能量是t0,t0=2.7 eV,n是原子链中原子的位置,P是对应原子的概率密度

3.3 能带分析

以上讨论了ZGNRs的电子态形式和性质,接下来我们分析能带结构和特点.ZGNRs的能带由驻波态的能带和边缘态的能带共同组成,如图3所示.根据驻波态能带关系(9)式,在一个周期单元kya0∈[-π,π]里,可知驻波态的能量E与cos(2ka)是单调递增的关系,能量E在cos(2ka)=1时有最大值,在cos(2ka)=-1时有最小值,因此驻波态能量E与无限长方向波矢ky的取值关系为

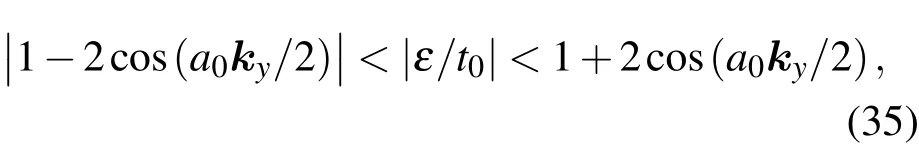
因此驻波态的能量值与ky的关系点都在该区间范围内.当N增大时,只是这个区间范围内点的密度越来越大,而不可能跑出这个区间.对于边缘态,根据波矢k的约束关系(31)和(34)式可得-N/(N+1)≤2cos(kya0/2)≤N/(N+1),因此在一个周期单元kya0∈[0,2π]里,边缘态的范围是

当N越大,也就是纳米带越宽时,含有边缘态的t取值范围越大,kya0的取值范围也越大,但无论如何t一定会在-t0—t0之间,即kya0∈(2π/3,4π/3);并且β=0时,t只有小于零时才有边缘态;β=π/2时,t只有大于零时才有边缘态.由能带(22)或(32)式可知,边缘态时能量的取值范围

一是组织完成了长江流域重要水功能区划分工作。成果已列入国务院批复的《全国重要江河湖泊水功能区划（2011-2030）》。

因此边缘态只有在低能态下存在,即在费米面附近.能带结构如图3所示,能带的条数是2N条,N是原胞数.当N很小时,能带关系只能取该区间中一些离散的能带,如图3(a)所示;随着N的增大,能够取到的能带越来越多,从图3(b)中可以看到,N=50时,基本上取到的点已经覆盖了整个区间,这时的能带结构和无限大的石墨烯能带结构基本上完全一样,除了边缘态的本征值外,就是图中加粗的红色部分.边缘态的能带关系只是导带底和价带顶的一小段能带,它是从驻波态能带中分离出来的;随着N的增大,边缘态的波矢量ky取值也增大,满足(36)式;同时,边缘态的能带将变得越来越陡峭,零能态对应的点增多,N=10时边缘态还是分叉型的,有很多本征值不为零的态,而N=50时基本上都是本征值为零的态了.我们选择β=0一端分析,N增大时,由(30)关系式有

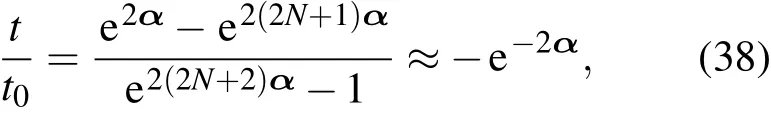
代入能带关系(22)式可知ε=0.因此随着N增大,更多的波矢α值满足(38)式,因此零能态的点增多,自然地能带关系变得陡峭.当ky=±π时,能带关系非常独特,所有的驻波态对应的能带都汇聚于点(±π,±t0),这意味着这些驻波态都是简并的;而边缘态的本征值为零,也是简并的,价带顶和导带底于(±π,0)处相交,从物理图像上看,此时t=0,因此二聚化原子链的超原胞将于有t相互作用处断开,波函数只能出现在边界处,或者出现在中间两两独立的格点处,而出现在边界处的波函数的线性组合就是边缘态,这时α趋于无穷大,出现在中间两两独立格点处的波函数的线性组合为驻波态.

图3 ZGNRs的能带结构图 (a)原胞数N=10;(b)原胞数N=50;ky的单位波矢为π/a0,E的单位能量是t0

3.4 电子态的过渡

在能带图像中我们发现：在价带顶或导带底这两条能带中,既包含了边缘态的能带,也包含了部分的驻波态能带,并且它们是连续过渡的.过渡点是ε=±t0/(N+1),在这两个本征值之间的能量对应的是边缘态,而在这两个本征值之外却都是驻波态,因此这两个本征值处的电子态非常独特,它是边缘态与驻波态转化的过渡点.从边缘态上看,由以上分析知α→0,β=0,π/2.为简单起见,我们选取β=0分析,波函数由(27)式得

归一化系数取三阶近似,化成

从驻波态上看,此时α=0,β→0,即ka→0,波函数由(16)式得

由(15)式知m为偶数,归一化系数也取三阶近似

由(39)—(42)式可知,在波矢量趋于零时,两类波函数具有相同的形式;两类波函数通过不同的方式在波矢量趋于零时逼近相同的形式,此时波函数关于相同格点位置呈线性关系,概率密度为二次函数关系.如图4所示,N=50时两类波函数趋于过渡点的情况,过渡点处由(36)式知kya0=0.67385π,1.32615π,已经很接近 2π/3,4π/3;能量值由 (37)式可得ε=±0.0196t0.从图4(a)和(b)可以看到,当能量小于相变点能量并逼近其时,边缘态中间处往上凹,电子的局域性变弱,两端处往下凹,边界的概率值减少;从图4(c)和(b)可以看到,当能量大于相变点能量并逼近其时,驻波态中间处往下凸,电子的局域性增强,两端处往上凹,边界的概率值增大.所以两类波函数通过不同的方式在波矢量趋于零时关于格点位置n逼近线性形式,如图4(b)所示.

图4 量子过渡点附近波函数的变化过程 (a)边缘态;(b)过渡点的电子态;(c)驻波态;其中n是原子链中原子的位置,Ψ是对应原子的波函数,ky的单位波矢为π/a0,E的单位能量是t0

4 结论

对于ZGNRs,在无限长方向应用Bloch定律,可以把它转化为对一个超原胞的求解,然后把超原胞化成二聚化原子链模型,应用有限系统的Bloch定理,可以解析地求出ZGNRs的电子态和能带.其电子态有两类,分别是驻波态和边缘态.驻波态中,其波矢为实数,波函数是正弦函数形式;边缘态时,其波矢主要是虚数,实数部分为零或者π/2,波函数是双曲正弦函数形式.同时我们得到了电子态的归一化系数和受限方向波矢的性质.其能带由驻波态能量和边缘态能量组成.我们推导得到了驻波态的最大允许的能带范围,还有边缘态的关于无限长方向波矢的精确取值范围和能量的精确取值范围;另外在讨论边缘态与驻波态的过渡点,我们发现两种电子态波函数通过不同的方式在受限波矢趋于零时关于格点位置逼近线性关系.当受限方向也变成无限长时,可以得到与无限大石墨烯相同的能带关系.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004 Science 306 666

[2]Das Sarma S,Adam S,Hwang E H 2011 Rev.Mod.Phys.83 407

[3]Novoselov K S,Geim A K,Morozov S V,Jiang D,Katsnelson M I,Grigorieva I V,Dubonos S V,Firsov A A 2005 Nature 438 197

[4]Geim A K,Novoselov K S 2007 Nat.Mater.6 183

[5]Katsnelson M I,Novoselov K S 2007 Solid State Commun.143 3

[6]Katsnelson M I 2007 Mater.Today 10 20

[7]Novoselov K S,Jiang D,Schedin F,Booth T J,Khotkevich V V,Morozov S V,Geim A K 2005 Proc.Nat.Acad.Sci.USA 102 10451

[8]Berger C,Song Z M,Li X B,Wu X S,Brown N,Naud C,Mayou D,Li T B,Hass J,Marchenkov A N,Conrad E H,First P N,de Heer W A 2006 Science 312 1191

[9]Liang X G,Fu Z L,Chou S Y 2007 Nano Lett.7 3840

[10]Li D,Mueller M B,Gilje S,Kaner R B,Wallace G G 2008 Nat.Nanotechnol.3 101

[11]Klein D J 1994 Chem.Phys.Lett.217 261

[12]Son Y W,Cohen M L,Louie S G 2006 Phys.Rev.Lett.97 216803

[13]Son Y W,Cohen M L,Louie S G 2006 Nature 444 347

[14]Sasaki K,Murakami S,Saito R 2006 Appl.Phys.Lett.88 113110

[15]Wakabayashi K,Sasaki K,Nakanishi T,Enoki T 2010 Sci.Technol.Adv.Mater.11 054504

[16]Ren S Y 2006 Electronic States in Crystals of Finite Size-Quantum Conf i nement of Bloch Waves(Beijing：Peking University Press)pp15—19(in Chinese)[任尚元2006有限晶体中的电子态——Bloch波的量子限域(北京：北京大学出版社)第15—19页]

[17]Ren S Y 2001 Phys.Rev.B 64 035322

[18]Ren S Y 2002 Ann.Phys.(N.Y.)301 22

[19]Ren S Y 2003 Europhys.Lett.64 783

[20]Zhang S B,Yeh C Y,Zunger A 1993 Phys.Rev.B 48 11204

[21]Zhang S B,Zunger A 1993 Appl.Phys.Lett.63 1399

[22]Ajoy A,Karmalkar S 2010 J.Phys.Condens.Matter 22 435502

[23]Jin Z F,Tong G P,Jiang Y J 2009 Acta Phys.Sin.58 8537(in Chinese)[金子飞,童国平,蒋永进2009物理学报58 8537]

[24]Wallace P R 1947 Phys.Rev.71 622