曾 波

（重庆工商大学 商务策划学院，重庆 400067）

一、引 言

1982年中国著名学者邓聚龙教授基于“灰箱”思想创立的灰色理论，是一种研究“小样本”、“贫信息”不确定性问题的新方法，主要通过对“部分”已知信息的生成和开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控［1］。灰色预测建模技术是灰色理论的重要组成部分，目前已被广泛应用于工业、农业、医学、军事等领域［2］。在应用过程中，研究人员根据解决问题的实际需要，不断地对灰色预测模型进行拓展与优化方面的大量研究，这些研究概括起来主要集中在：

第一，建模序列预处理方法研究［3－4］。通过缓冲算子弱化冲击扰动对模型构造的影响；通过序列函数变换提高建模序列光滑度，从而优化模型精度。

第二，模型参数优化方法研究［5－6］。通过数学方法优化模型初始值与背景值，从而优化灰色预测模型建模参数a，b，提高模型模拟及预测精度。

第三，建模方法拓展研究［7－8］。以 GM（1，1）模型为基础，根据实际情况对既有建模方法进行拓展，比较有代表性的是离散灰色预测模型。

第四，建模对象拓展研究［9－10］。将灰色预测模型建模对象拓展至非等间隔序列以及从实数拓展区间灰数与离散灰数方面的研究。

第五，模型建模机理研究［11－12］。对建模序列灰色生成方法研究；模型稳定性及产生病态性条件研究；模型建模条件与适用范围研究等。

第六，其他相关研究［13－15］。包括将灰色预测模型与其他模型或方法进行组合，从而构建新预测模型方面的研究和模型误差检验方法研究等。

上述研究在较大程度上促进了灰色预测建模技术的发展，但作为一种新的预测建模技术，其理论体系还有待于进一步丰富和完善。纵观灰色预测模型的既有研究成果，主要围绕以“实数”为建模对象的经典灰色预测模型、以“区间灰数”为建模对象的区间灰数预测模型、以“离散灰数”为建模对象的离散灰数预测模型展开相关研究，对建模序列中同时包含“实数”及“区间灰数”等数据类型不一致的“灰色异构数据序列”，尚无有效建模方法和预测手段。基于此，笔者将对建模序列中同时包括“实数”及“区间灰数”的双重异构数据预测建模方法展开研究，从而将灰色预测模型建模对象从“同质数据”拓展至“异构数据”。

二、基本概念

定义2 设＝（x1，x2，…，xn）为灰色异构数据序列，当 中不同数据类型的个数为2时，则称为灰色双重异构数据序列；当 中不同数据类型的个数为3及其以上时，则称 为灰色多重异构数据序列。

推论1 根据定义3可知，实数的“核”即为实数本身，信息域为0。

公理1 （灰度不减公理）两个灰度不同的区间灰数进行和、差、积、商运算时，运算结果的灰度不小于灰度较大的区间灰数的灰度［16］。

根据公理1，可得如下两个推论：

推论2 一个实数与一个区间灰数进行和、差、积、商运算时，运算结果的灰度与区间灰数的灰度相同。

推论3 两个信息域不同的区间灰数进行和、差、积、商运算时，运算结果的信息域不小于信息域较大的区间灰数的信息域。

三、模型构建

!据序列X中较大的区间灰数信息域作为预测结果的信息域（根据推论3）；最后，结合定义3中的内容，构建双重异构数据序列的灰色预测模型。

（一）双重异构数据核序列的DGM（1，1）模型

将式（3）、（4）代人式（2），整理后最终可得如下齐次指数函数：

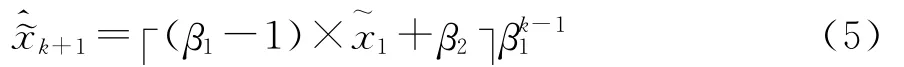
式（5）被称为双重异构数据“核”序列 DGM（1，1）模型的最终还原式，由于（β1－1）×＋β2为一常数，

（二）信息域的确定

根据推论3，通常可将双重异构数据序列中信息域较大的区间灰数的信息域作为预测结果的信息域。

（三）模型推导

联立式（6）、（8）、（9）组合方程组得：

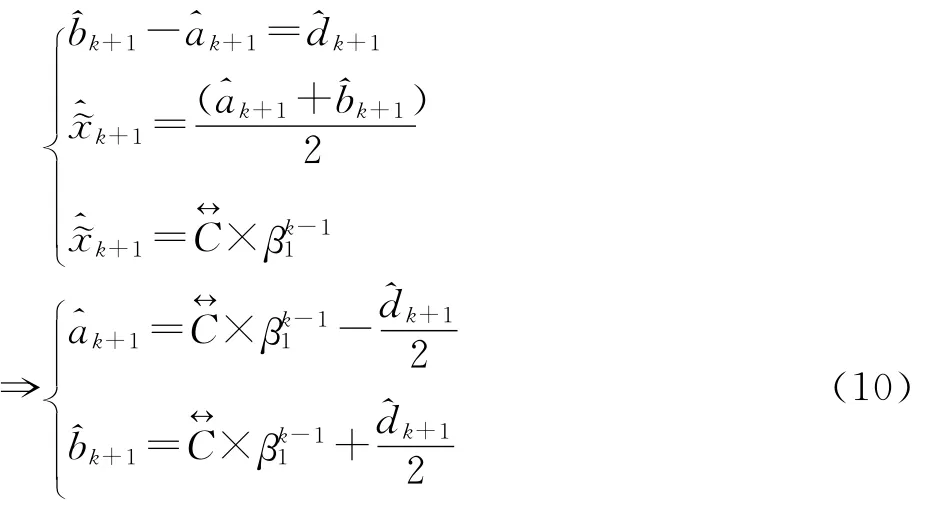
式（10）称为单变量一阶双重异构数据灰色预测模型，为表述方便，后文简称 DHGM（1，1）（Double Heterogeneous Grey Model）。

四、DHGM（1，1）模型与传统DGM（1，1）模型的关系

DHGM（1，1）模型与传统 DGM（1，1）模型同属灰色预测模型，二者的区别在于建模对象存在差异，前者为“灰色双重异构数据”序列，而后者为“实数”序列。因实数序列是灰色双重异构数据序列的一种特殊情况，故DHGM（1，1）模型是DGM（1，1）模型在建模对象方面的拓展与延伸，当DHGM（1，1）模型建模序列中元素全部变为实数时，DHGM（1，1）模型与传统 DGM（1，1）模型应该具有完全相同的时间响应式，本小节就对DHGM（1，1）与DGM（1，1）的这种关系进行推导。

当灰色双重异构数据序列中的元素全部变为实数时，由于实数属于“白数”，信息完全已知，其灰度为0，故其信息域为0，即：

根据式（10）可知，当预测对象的信息域为0时，可推出：

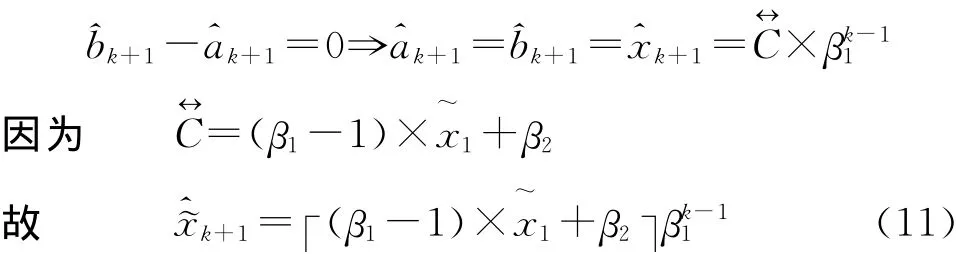
根据式（5）可知，式（11）即为 DGM（1，1）模型的时间响应式。可见当DHGM（1，1）模型建模序列中元素全部变为实数时，DHGM（1，1）模型与DGM（1，1）模型具有完全相同的时间响应式。传统DGM（1，1）模型是DHGM（1，1）模型的一种特殊情况，只有当建模序列中的元素均为实数这一特殊情况时才能被用于预测，而当建模对象中的元素同时包含“实数”及“区间灰数”等数据类型不一致的灰色双重异构数据序列时，就可使用DHGM（1，1）模型来实现数据预测。因此，DHGM（1，1）模型拓展了DGM（1，1）模型的应用范围，更具普适性。

五、模型应用举例

自然灾害的非常规性、突发性和不确定性，决定了救援机构在较短时间内难以采集到精确的大样本统计数据，单凭某一途径所获得的有限信息，难以实现对自然灾害发展趋势的全面客观认识。在这样的情况下，通过多源信息集结提高样本数据可信度对灾害应急救援具有重要作用，然而信息来源的多样性往往造成集结信息数据类型不一致、不兼容，从而形成了包含不同数据类型的灰色异构数据序列。地震发生后某药品需求量统计数据如表1所示。

表1 某药品在不同时点需求数量表

试根据表1，构建灰色异构数据的DHGM（1，1）模型，并预测时点7的药品需求数量。

在本例中，首先对表1中各个时点数据的“核”进行计算，计算结果构成“核”序列；然后通过建立“核”序列的 DGM（1，1）模型，实现双重异构数据“核”的预测；再以“核”的预测结果为基础，以表1中较大的区间灰数信息域作为预测结果的信息域；最后应用公式（10），即本文所研究的DHGM（1，1）模型，构建基于区间灰数与实数的双重异构数据序列地震药品需求量预测模型。在此基础上，实现对时点7药品需求数量的预测。

步骤1“核”序列的计算及其 DGM（1，1）模型的构建。

根据定义3，的核序列为：

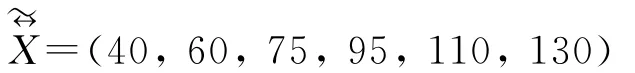
根据式 （6），X（）的 DGM（1，1）模型还原式为：

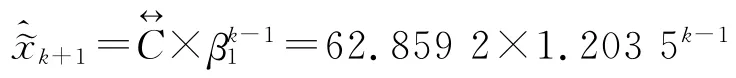
其中β1＝1．203 5，β2＝54．717 9。核序列平均相对误差Δ－＝0．462 4%，对照灰色系统预测模型的精度检验等级参照表可知［16］169－190，模型的平均相对误差小于1%，表明该模型可用于灰色异构数据核的预测。

步骤2 信息域的确定。

步骤3 模型的建立与预测。

根据式（10），构建基于实数与区间灰数的DHGM（1，1）模型，如下：

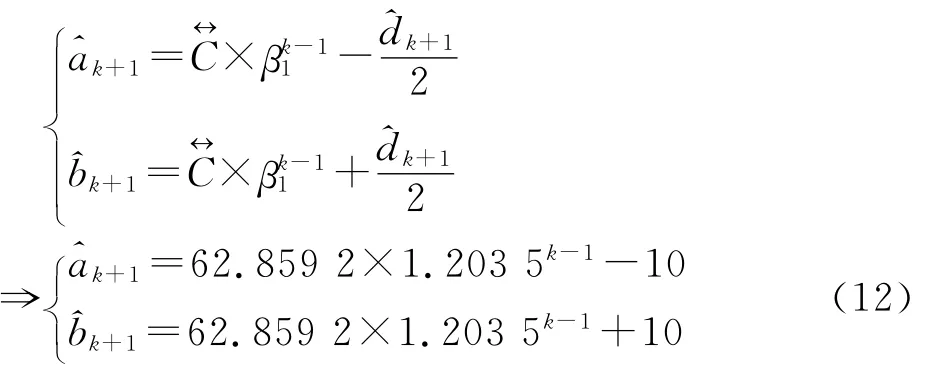
根据式（12），预测时点7的药品需求数量人数，即当k＝6、预 测＝148．7、＾b6＝168．7，则∈［148．7，168．7］＝（a7＋b7）／2＝158．7。

六、结 论

灰色预测建模技术是灰色系统理论最重要的组成部分之一，是研究“小样本”、“不确定性”问题的常用方法。然而，目前灰色预测模型的既有研究成果，主要围绕以“实数”为建模对象的经典灰色预测模型、以“区间灰数”为建模对象的区间灰数预测模型、以“离散灰数”为建模对象的离散灰数预测模型展开相关研究，对于建模序列中同时包含“实数”与“区间灰数”等数据类型不一致的“灰色异构数据序列”，尚无有效的建模方法和预测手段。鉴此，本文通过建立灰色异构数据“核”序列的DGM（1，1）模型，实现双重异构数据“核”的预测；以“核”为基础，以双重异构数据序列中较大的区间灰数信息域作为预测结果的信息域，构建了基于区间灰数与实数的双重异构数据序列灰色预测模型，从而有效地将灰色预测模型建模对象，从“同质数据”拓展至“双重异构数据”，对丰富灰色预测模型理论体系具有积极意义。

［1］ Deng J L．The Control Problem of Grey Systems［J］．System Control Letter，1982（5）．

［2］ Deng Julong．Introduction to Grey System Theory［J］．The Journal of Grey System （UK），1989（1）．

［3］ 崔立志，刘思峰，吴正鹏．新的强化缓冲算子及其应用［J］．系统工程理论与实践，2010（3）．

［4］ 关叶青，刘思峰．基于函数cot（xα）变换的灰色 GM（1，1）建模方法［J］．系统工程，2008（9）．

［5］ Dang Y G，Liu S F．The GM Models That x（n）be Taken as Initial Value［J］．The International Journal of Systems ＆Cybernetics，2004（2）．

［6］ Wang Z X，Dang Y G，Liu S F．The Optimization of Background Value in GM （1，1）Model［J］．The Journal of Grey System，2007（2）．

［7］ Xie N M，Liu S F，Discrete Grey Forecasting Model and its Optimization［J］．Applied Mathematical Modeling，2009（1）．

［8］ Deng J L．Undulating Grey Model GM（1，1｜tan（k－τ）p，sin（k－τ）p）［J］．Journal of Grey System，2001（3）．

［9］ 曾波，刘思峰．一种基于区间灰数几何特征的灰数预测模型［J］．系统工程学报，2011（2）．

［10］张军，曾波．区间灰数序列的白化方法及其性质研究［J］．统计与信息论坛，2012（8）．

［11］Deng J L．Negative Power AGO in Grey Theory［J］．Journal of Grey System，2001（3）．

［12］Song Z M，Xiao X P，Deng J L．The Character of Opposite Direction AGO and Class Ratio［J］．The Journal of Grey System，2002（1）．

［13］曾波，刘思峰．基于灰色关联度的小样本预测模型［J］．统计与信息论坛，2009（12）．

［14］Li G D，Daisuke Y，Masatake N．A GM（1，1）Markov Chain Combined Model With an Application to Predict the Number of Chinese International Airlines［J］．Technological Forecasting and Social Change，2009（8）．

［15］王正新，党耀国，裴玲玲．灰色 GM（1，1）幂模型初始条件的组合优化［J］．统计与信息论坛，2012（6）．

［16］Liu S F，Lin Y．Grey Systems Theory and Applications［M］．Berlin Heidelberg：Springer－Verlag，2010．