张雄伟

榆林学院 数学系，陕西 榆林 719000

剩余格上的模糊软滤子

张雄伟

榆林学院 数学系，陕西 榆林 719000

模糊集、粗糙集、Vague集等理论，在处理不确定性问题时，都具有相同的不足之处，即参数工具理论的不充[1]。为此，在1999年，Molodtsov提出了基于参数集的软集的概念[1]。此后，许多学者先后将软集应用到决策分析[2-4]、模糊软集[5-6]、区间值模糊软集[7]、模糊软群[8]上。本文给出了剩余格上的模糊软滤子，然后对它们的性质进行了研究，此外，定义了剩余格上的模糊软滤子间的模糊软同态和模糊软同构，给出了剩余格上的模糊软滤子的同构像定理和同态逆像定理。

1 预备知识

下面给出一些关于模糊软集和剩余格的有关知识。

定义1.1[5]设X是一个论域，X上的一个模糊软集是一个偶对(f，A)（这里A⊆E且E是一个非空参数集），且f:A→IX是一个映射，即对于每一个e∈A，f(e)=fe:X→I是X上的模糊集合。

定义1.2[5]设X上的两个模糊软集(f，A)和(g，B)，(f，A)是(g，B)的模糊软子集，是指：

（1）A⊆B；（2）∀e∈A，fe≤ge，即fe是ge的模糊子集。记为：(f，A)⊆(g，B)。

定义1.3[5]设X上的两个模糊软集(f，A)和(g，B)，(f，A) 和(g，B)是相等的模糊软集，是指(f，A)⊆(g，B)且(g，B)⊆(f，A)。

定义1.4[5]设X上的两个模糊软集(f，A)和(g，B)，(f，A) 和(g，B)的并是一个模糊软集(h，C)，这里的C=A∪B且

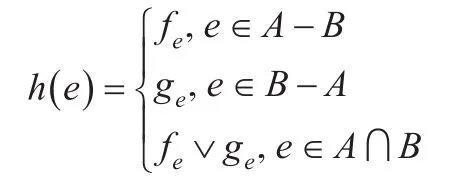
记为(f，A) ∪(g，B)=(h，C)。

定义1.5[5]设X上的两个模糊软集(f，A)和(g，B)，(f,A)和(g,B)的交是一个模糊软集(h，C)，这里的C=A∩B且he=fe∧ge(∀e∈C)。记为(f，A)∩(g，B)=(h，C)。

定义1.6[5]设X上的两个模糊软集(f，A)和(g，B)，(f,A)AND(g，B)记为(f,A)∧(g,B)，具体定义为(h，A×B)，这里的h(a，b)=ha，b=fa∧gb(∀ (a，b)∈A×B)。

定义1.7[8]设(f，A)和(g，B)分别是X和Y上的模糊软集，Ξ是X到Y的函数，Θ是从参数A到参数B的函数，定义(Ξ，Θ)如下：(Ξ，Θ)(f，A)=(Ξ(f)，Θ(A))，这里Ξ(f)a满足：对于任意的a∈Θ(A)，∀y∈Y：

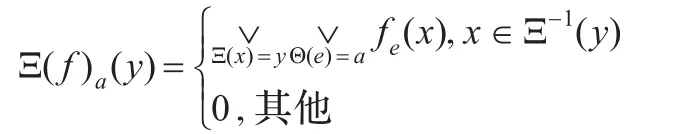
定义 (Ξ，Θ)-1(g，B)=(Ξ-1(g)，Θ-1(B))，这里的 Ξ-1(g)e(x)=gΘ(e)(Ξ(x)) (∀e∈Θ-1(B)，∀x∈X)这时称偶对(Ξ，Θ)是从X到Y上的模糊软函数，并称(Ξ，Θ)(f，A)是(f，A)在模糊软函数(Ξ，Θ)下的像，(Ξ，Θ)-1(g，B)是(g，B)在模糊软函数(Ξ，Θ)下的原像。

设{(fk，Ak)|k∈K，Ak⊆E}是X上的一族非空模糊软集合，即，对于每一个e∈Ak，fk(e)=fke:X→I是X上的模糊集，记做(f，A)k=(fk，Ak)(∀k∈K)。

定义1.8[9]设(f，A)k是X上的一族非空模糊软集合，定义并∪k∈K(f，A)k和交∩k∈K(f，A)k是X的两个模糊软集合(h，C)和(g，B)如下：

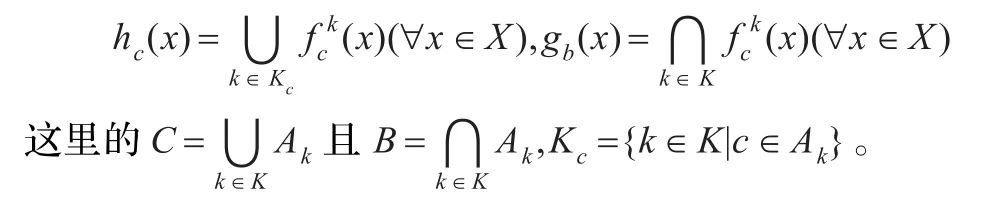
定义1.9[10-15]一个剩余格是一个（2，2，2，2，0，0）型代数L=(L，∧，∨，⊗，→，0，1)，满足：（1）(L，∧，∨，0，1)是一个有界格，并分别以0，1为最小元和最大元；（2）(L，⊗，1)是一个交换幺半群，且运算⊗保序；（3）a⊗b≤c当且仅当a≤b→c(∀a，b，c∈L)。

性质1.10[10-15]设L是一个剩余格，则

(R1)a⊗b≤a∧b

(R2)a→(b∧c)=(a→b)∧(a→c)

(R3)(a∨b)→c=(a→c)∧(b→c)

(R4)a⊗(b∨c)=(a⊗b)∨(a⊗c)

(R5)b→c≤(a→b)→(a→c)

(R6)a=1→a

(R7)a≤b当且仅当a→b=1

(R8)a≤b→c当且仅当b≤a→c

(R9)a→(b→c)=b→(a→c)=(a⊗b)→c

(R10)a→b≤(a⊗c)→(b⊗c)

(R11)a→b≥b

(R12)b≥a⊗(a→b)

(R13)b≤a→(a⊗b)

(R14)a→(a⊗b)≤a→b

(R15)a≤(a→b)→b

(R16)(a→b)⊗(b→c)≤a→c

定义1.11[10-15]剩余格上L的非空子集F称为一个滤子，如果（F1）F是一个上集，即若x≤y，则x∈F蕴含y∈F；（F2）F对⊗关闭，即若x，y∈F，则x⊗y∈F。

命题1.12[10-15]设F是L的非空子集。则下面三条等价：

（1）F是一个滤子；

（2）1∈F且∀x，y∈L，x，x→y∈F蕴含y∈F；

（3）F对⊗关闭且∀x∈F，y∈L，有x∨y∈F。

2 剩余格上的模糊软滤子

定义2.1设L是一个剩余格，(f，A)是L上的一个模糊软集合，如果满足∀x，y∈L，e∈A，（1）fe(1)=1；（2）fe(y)≥fe(x)∧fe(x→y)。则称(f，A)是L上的一个模糊软滤子，即每一个e∈A，fe是L上的模糊滤子（文献[10]意义下的）。L上所有模糊软滤子的全体记为：FSF(L)，显然(FSF(L),⊆)是偏序集。

例2.2设L={0，a，b，1}，0≤a≤b≤1，ℕ是所有自然数集的集合，定义⊗和→如下（图1）：可以验证L是一个剩余格，定义f:ℕ→IX如下：fn(x)=1(∀n∈ℕ)，则偶对(f,ℕ)是X上的一个模糊软集，显然(f，ℕ)是L上的一个模糊软滤子。

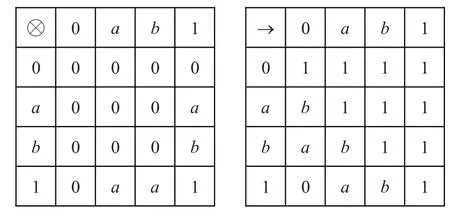
图1 剩余格上的两种运算⊗和→

定理2.3设(f，A)和(g，B)是L上的两个模糊软滤子，则(f，A)∩(g，B)是L上的一个模糊软滤子。

证明设(f，A)∩(g，B)=(h，C)，这里的C=A∩B且he=fe∧ge(∀e∈C)，

（1）∀x∈L，he(1)=(fe∧ge)(1)=fe(1)∧ge(1)=1

（2）∀x，y∈L，he(y)=(fe∧ge)(y)=fe(y)∧ge(y)≥fe(x)∧fe(x→y)∧ge(x)∧ge(x→y)=he(x)∧he(x→y)

所以(f，A) ∩(g，B)是L上的一个模糊软理想。

定理2.4设(f，A)和(g，B)是L上的两个模糊软滤子，则(f，A)AND(g，B)是L上的一个模糊软滤子。

证明设(f,A)AND(g，B)=(h,A×B)，这里的h(a,b)=ha，b=fa∧gb(∀ (a，b)∈A×B)。对每一个(a，b)∈A×B，由于(f，A)和(g，B)是L上的两个模糊软滤子，有：

（1）∀x∈L，ha，b(1)=(fa∧gb)(1)=fa(1)∧gb(1)=1

（2）∀x,y∈L，ha,b(y)=(fa∧gb)(y)=fa(y)∧gb(y)≥fa(x)∧fa(x→y)∧gb(x)∧gb(x→y)=ha，b(x)∧ha，b(x→y)

所以(f，A)AND(g，B)是L上的一个模糊软滤子。

定理2.5设(f，A)和(g，B)是L上的两个模糊软滤子，则(f，A)∪(g，B)是L上的一个模糊软滤子。

证明设(f，A)∪(g，B)=(h，C)，若e∈A-B，则he=fe，由定义2.1知(f，A)是L上的模糊滤子；若e∈B-A，则he=ge，由定义2.1知(g，B)是L上的模糊滤子；若e∈A∩B，则he=fe∨ge，有：

（1）∀x∈L，he(1)=(fe∨ge)(1)=fe(1)∨ge(1)=1

（2）∀x,y∈L,he(y)=(fe∨ge)(y)=fe(y)∨ge(y)=max{fe(y)，ge(y)}，不失一般性，设fe(y)≤ge(y)，则he=ge，所以he(y)=ge(y)≥ge(x)∧ge(x→y)=he(x)∧he(x→y)，因此(f,A)∪(g,B)是L上的一个模糊软滤子。

类似定理2.3和定理2.5，可以证明的定理：

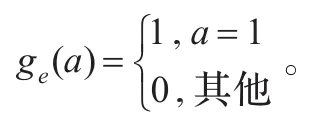
3 剩余格上的模糊软滤子间的同态

定义3.1设(Ξ，Θ)是从剩余格X到剩余格Y上的模糊软函数，若Ξ满足Ξ(x→y)=Ξ(x)→Ξ(y)，(∀x，y∈X)，则称(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同态；若(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同态，Ξ是从X到Y的一一映射且Θ是从A到B的一一映射，则称(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同构。

定理3.2设(g，B)是剩余格Y上的模糊软滤子，(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同态，则(Ξ，Θ)-1(g，B)是剩余格Y上的模糊软滤子。

证明注意到(Ξ，Θ)-1(g，B)=(Ξ-1(g)，Θ-1(B))，所以对于任意的e∈Θ-1(B)，有：

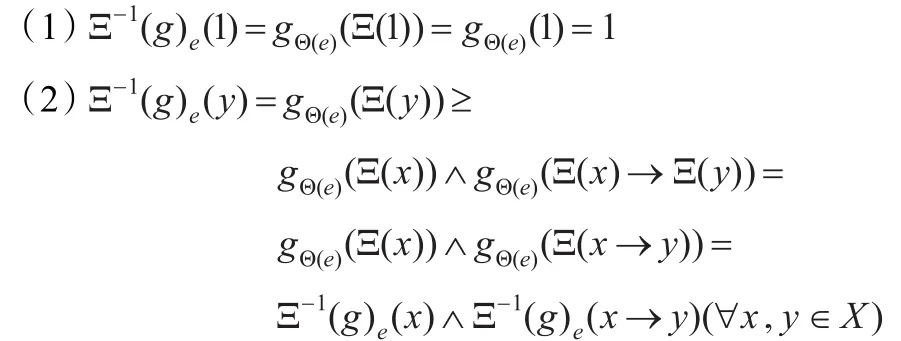
所以(Ξ，Θ)-1(g，B)是剩余格Y上的模糊软滤子。

定理3.3设(f，A)是剩余格X上的模糊软滤子，(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同构，则(Ξ，Θ)(f，A)是剩余格Y上的模糊软滤子。

证明注意到(Ξ，Θ)(f，A)=(Ξ(f)，Θ(A))，设a∈Θ(A)且y，x∈Y，由于(Ξ,Θ)是剩余格X到剩余格Y上的模糊软滤子间的同构，则存在唯一的y1，x1∈X使得Ξ(y1)=y，Ξ(x1)=x，和唯一的e∈A使得Θ(e)=a，这时有，因此Ξ(f)a(1)=1，同时也有：

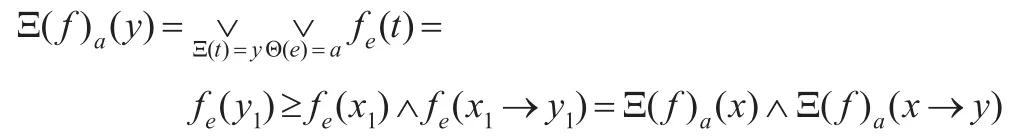
因此(Ξ，Θ)(f，A)是剩余格Y上的模糊软滤子。

问题3.4定理3.3中如果只要求(Ξ，Θ)是剩余格X到剩余格Y上的模糊软滤子间的同态，那么(Ξ，Θ)(f，A)是剩余格Y上的模糊软滤子吗？

4 结束语

关于软集理论的研究与应用受到了众多学者越来越多的关注。本文提出了剩余格上的模糊软滤子的概念，并研究了它的一些性质，根据文献的结果，也可以定义剩余格上的模糊软理想和模糊软同余，研究其性质，由于方法类似不再这里赘述。

[1]Molodtsov D.Soft set theory—first results[J].Computers and Mathematics with Applications，1999，37（4/5）：19-31.

[2]Maji P K，Biswas R，Roy A R.Soft set theory[J].Computers and Mathematics with Applications，2003，45（4/5）：555-562.

[3]Feng feng，Jun Y B，Liu Xiaoyan，et al.An adjustable approach to fuzzy soft set based decision making[J].Journal of Computational and Applied Mathematics，2010，234（1）：10-20.

[4]Kong Z，Gao Liqun，Wang Lifu.Comment on“A fuzzy soft set theoretic approach to decision making problems”[J].Journal of Computational and Applied Mathematics，2009，223（2）：540-542.

[5]Maji P K，Biswas R，Roy A R.Fuzzy soft sets[J].Journal of Fuzzy Mathematics，2001，9（3）：589-602.

[6]Majumdar P，Samanta S K.Generalised fuzzy soft sets[J]. Computers&Mathematics with Applications，2010，59（4）：1425-1432.

[7]Yang Xibei.Combination of interval valued fuzzy set and soft set[J].Computers and Mathematics with Applications，2009，58（3）：521-527.

[8]Aygu¨nog˘luA，Aygu¨n H.Introduction to fuzzy soft groups[J]. Computers&Mathematics with Applications，2009，58（6）：1279-1286.

[9]Tanay B，Kandemir M B.Topological structure of fuzzy soft sets[J].Computers and Mathematics with Applications，2011，61：2952-2957.

[10]Höhle U.Commutative residuated monoid[M]//Höhle U，Klement E P.Non-classical Logics and Their Applications to Fuzzy Subsets.Dordrecht：Kluwer Academic Publishers，1995：53-106.

[11]Ward M，Dilworth R P.Residuated lattices[J].Trans on Amer Math Soc，1939，45：335-354.

[12]Hájek P.Mathematics of fuzzy logic[M].Dordrecht：Kluwer Academic Publishers，1998.

[13]Zhu Y Q，Xu Y.On filter theory of residuated lattices[J].Information Science，2010，180：3614-3632.

[14]刘春辉，徐罗山.关于剩余格的理想[J].山东大学学报：理学版，2010，45（4）：66-71.

[15]裴道武.剩余格与正则剩余格的特征定理[J].数学学报，2002，45（2）：271-278.

ZHANG Xiongwei

Department of Mathematics,Yulin University,Yulin,Shaanxi 719000,China

Molodtsov introduces the concept of soft set theory which can be used as generic mathematical tool for dealing with uncertainty.The notions of a fuzzy soft filters in residuated lattices are given.Some of their properties are studied.Furthermore, definitions of fuzzy soft homomorphism and fuzzy soft isomomorphism of fuzzy soft ideals in residuated lattices are defined and the theorems of isomomorphic image and homomorphic pre-image of fuzzy soft ideals in residuated lattices are given.

fuzzy set;fuzzy soft set;residuated lattices;fuzzy soft filters

Molodtsov引入的软集理论，可作为通用的数学工具去处理不确定性问题。给出了剩余格上的模糊软滤子，对它们的性质进行了研究，此外，定义了剩余格上的模糊软滤子间的模糊软同态和模糊软同构，给出了剩余格上的模糊软滤子的同构像定理和同态逆像定理。

模糊集；模糊软集；剩余格；模糊软理想

A

TP18

10.3778/j.issn.1002-8331.1304-0380

ZHANG Xiongwei.Fuzzy soft ideals on residuated lattices.Computer Engineering and Applications,2013,49（18）：45-47.

国家自然科学基金（No.11071151）；陕西省教育厅科学研究计划项目（No.12Jk0890）。

张雄伟（1979—），男，硕士，主要从事格上拓扑学的研究。E-mail：zhangxw1019@163.com

2013-04-26

2013-05-30

1002-8331（2013）18-0045-03