WANG Lili ，XIONG Jingqi，HAN Xing，QIN Xiaopin

University of Electronic Science and Technology，Chengdu 611731，China

1.Introduction

Roller bearing is one of the most wildly used parts in modern machinery and equipment，but it is also prone to failure which could affect the operation of equipment and economic benefits，even bring about production accident or critical human injuries.Therefore，fault diagnosis for roller bearings is significant.

In the process of running，the contact between an impaired point of a damaged bearing and the surface of adjacent part would cause an impact，whose frequency is called fault feature frequency of bearing.This frequency can be used for bearing troubleshooting and the key is to extract the fault feature parameters，which relates to the accuracy of fault diagnosis.Because the early fault signal is weak，work environment and the bearing itself have affected，and measurement process causes noisy pollution，it’s very difficult to extract the signal feature.It means that denoising for the early signal is a very important task.

Wavelet thresholding de-noising［1-2］proposed by Donoho［3］，namely soft thresholding and hard thresholding，has wildly used［4］.But in 1995，Brace and Gao have proved that the hard thresholding always has a quite large variance mainly due to discontinuity，and soft thresholding also has a deviation because of making the part over the system range shrink.For these reasons，many improved threshold methods［5-7］have been proposed so far.This paper describes an improved thresholding method，the optimized threshold method based on relevant principles，and confirms its advantages compared to the traditional de-noising method，and then propose a new de-noising method.Morphological wavelet can be applied to de-noisy signal and extract fault feature.It evidently increases the efficiency of working and accuracy of fault feature extraction

2.The optimized threshold method based on relevant principles

Fault information always implicit in low frequency signal or some stationary signal and noisy usually is high frequency signal.So according to signal characteristic，using wavelet transformation can decompose these signal into different scale(correspond different frequency bands)，then wavelet decomposition coefficients processing and reconstruction can achieve the purpose of de-noising.

In strong noisy interference，the wavelet coefficient of the useful signal is often higher than the noisy signal，so using the same threshold to process the coefficient maybe blot out the useful signal.The traditional de-noising method has defects which makes fault feature extraction has obvious deviation.For this reason，we propose a threshold optimization method，that means to design the weight series matrix based on the relevance of wavelet coefficients in the corresponding position of each decomposed layer and optimize the weights of threshold，in order to make the de-noising thresholds of each level and each point more accurate，thus improve de-noising effect and maintain the useful signal more completely and enhance its the capacity of anti-interference.

3.The theory of the optimized threshold method based on relevant principles

The different propagation characteristics between the signal and the noisy in each scales indicate that the signal wavelet transform has strong correlation and so does its edge，but the noisy doesn’t.Because the signal is mainly distributed in low frequency or low scale part，while the noise is predominant relative to the signal in high frequency or high scales part.Wavelet transformation has a strong de-correlation.However，after transformed，each wavelet coefficient still keeps much correlation.It means that corresponding coefficients of wavelet coefficient have quite strong relevance in different resolutions.Low resolution coefficients and high resolution coefficients are correlated，what is the inter-scale dependency.Based on the different characteristic shown in each scale range between the signal and the noisy，we can use the correlation to locate the signal wavelet decomposition coefficients in order to make optimization to the range of the signal.

Defined correlative quantities of the adjacent scales wavelet coefficients in the same spatial position is the product of those adjacent scales coefficients，denoted as:

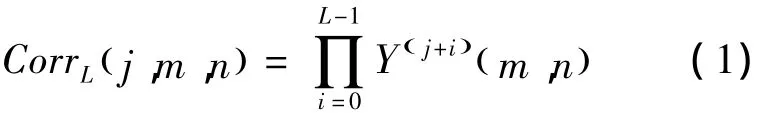
WhereLis the coefficient for calculation of the product，(m，n)means the spatial position of the coefficient(extend sub-band coefficients to the same scale before product)，andJmeans the scale.Because the location of some edge features will deviate with the scale changing，traditional threshold de-noising method is easy to remove the signal and the noisy simultaneously with using the same threshold for each level.In order to solve the problems of traditional thresholding，the optimized threshold method based on relevant principles calculates the correlation coefficient，reduces the threshold in the position of large correlation coefficients，and enlarges the threshold in the position of small correlation coefficients，and sets a weight to each threshold of the wavelet coefficients in order to adjust the threshold.

4.Simulation of the optimized threshold method based on relevant principles

In order to compare the cons and pros of this method with that of the traditional method，we treat the fault signal for simulation de-noising in different ways.Firstly，simulate the fault impact signal of the out ring of the bearing，shown in Fig.1(a)，and overlay it with a low frequency interference and a few of Gaussian white noise to get the noisy signal，shown in Figure 1(b)，then use the traditional thresholding and threshold optimization method respectively based on some relevant principles to de-noise and get the result shown in Fig.1(c)，1(d).

As we see in Figure 1(c)，after traditional threshold de-noised，its signal has a lot of low frequency inference without obvious periodicity，the peck?of the signal cannot be clearly reflected.The signal lack fidelity so severely that impede judgment to the fault feature.In Figure 1(d)，we can accurately extract the signal feature value by using the optimized threshold method based on relevant principles，low-frequency interference is substantially completely eliminate，the simulation signals in figure 1 can re-flect the advantage that this improved algorithm will get more complete fault features clearly，what is to say that this method has significantly improved compared with traditional thresholding method.

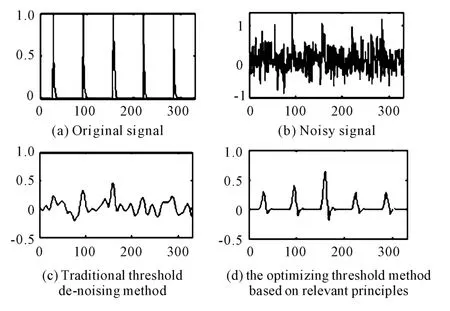
Fig.1 De-noising effect of the optimized threshold method based on relevant principles

5.Morphological wavelet de-noising

Different with the previous improved method that do some optimization to traditional wavelet threshold value，we take advantage of the morphological wavelet nonlinear filtering features，apply it to the signal de-noising and fault feature extraction for bearing fault diagnosis，and compare its De-noising effect with the optimized threshold method based on relevant principles in practice，descript its advantages and disadvantages.

6.Transform theory of dual wavelet

The difference between Morphological wavelet and traditional classical linear wavelet transform is that using corrosion or dilation operator instead of the original linear decomposition operator.According to the nonlinear wavelet framework and the signal decomposition theory proposed by Goutsias and Heijmans［8］.Assuming geometricVjandWjrespectively represent the j-th layer signal space and detail space.Signal analysis refers to signal analysis operator:Vj→Vj+1and detail analysis of operator:Vj→Wj+1decompose along the direction ofjincreasing.Signal synthesis refers toVj+1×Wj+1→Vjsyntheticalong the direction ofjdecreasing.This decomposition scheme is the dual wavelet decomposition.As shown in Fig.2.

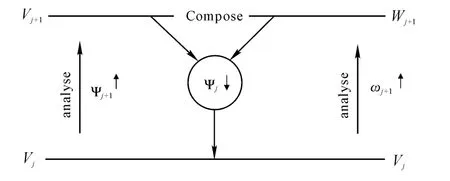
Fig.2 dual wavelet decomposition

The condition of the signal perfect reconstruction:

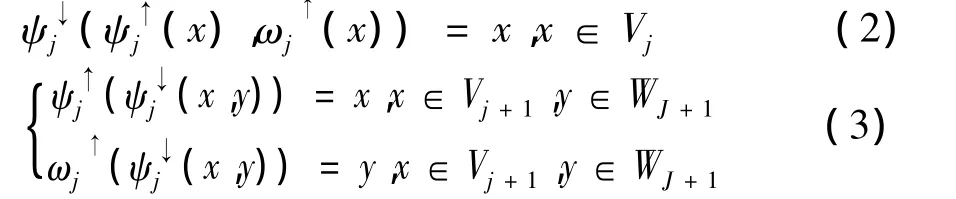
Formula(3)is the condition for wavelet decomposition perfect reconstruction.formula(4)is the wavelet pyramid conditions which ensure that the wavelet decomposition and reconstruction process without loss of information.

Assume that there is a plus operatorin the signal space as well as operator:Vj+1→Vjand:W→Vmeet the conditions:j+1j

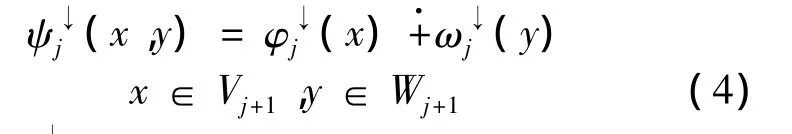
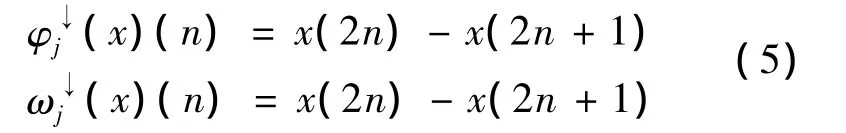
The basic ideas of Morphological Wavelet is when using the wavelet algorithm，using nonlinear morphological operator to replace the original linear operator，in order to realize nonlinear filtering.

7.Decomposition method of Morphological Wavelet

The basic principles of morphological wavelet transform and some major nature are introduced above.from the morphological wavelet applicability，the morphological wavelet applied to nonlinear timevarying signal analysis is feasible.Using different operator can get different morphological filter.In this paper，morphological median wavelet was adopted，which based on partly features of signals to signal decomposition，with updates to the adaptive nature of sense.

Suppose A is a structural element，the one-di-mensionalmorphological median operatorcan be obtained as:

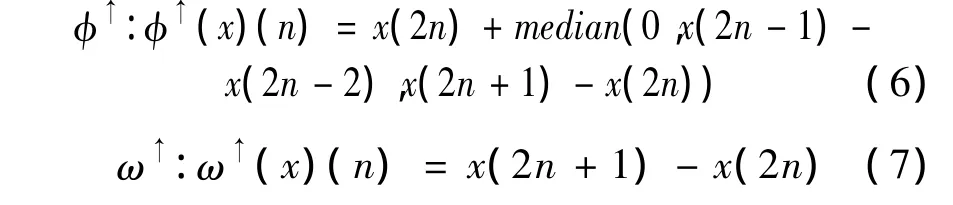
Composite operator is:

8.Simulation and analysis results

In order to verify the application features to extract the signal impact component of morphologicalwavelet，compared its de-noising effect with the optimized threshold method based on relevant principles，and illustrate whetherthe morphologicalwavelet method is better.Then we analyze specific instances of fault signal diagnosis.In order to analyze the denoising capacity of improved algorithm to the actual bearing fault，we use the bearing failure experimental data from Case Western Reserve University，The specific parameters listed in Tab.1.

Tab.1 main parameters of experimental platform

Experiments bearing speed is 1 797 r/min，sampling frequency is 12 000 Hz.Failure is the inner ring fault，fault diameter is 0.178 mm，fault depth is 0.28 mm.

Characteristic frequency:

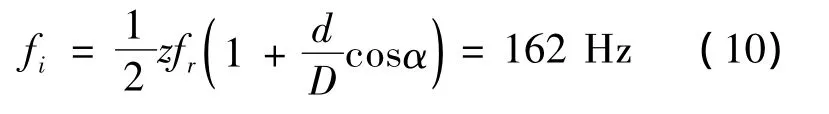
α is bearing contact angle，zis number of rolling elements.

Fig.3 is the time-domain waveform graph including the original signal and de-nosing signal.

In Fig.3，by comparing the time domain waveform figure to each other，we can see that two methods are effective for noise elimination，the fault featuresand frequency doubling composition of the morphological wavelet is more prominent than the optimized threshold method based on relevant principles.However，if just according to the time-domain waveform analysis，we can’t observe the fault feature.Therefore，the collected signal needs spectrum analysis as shown in Fig.4.

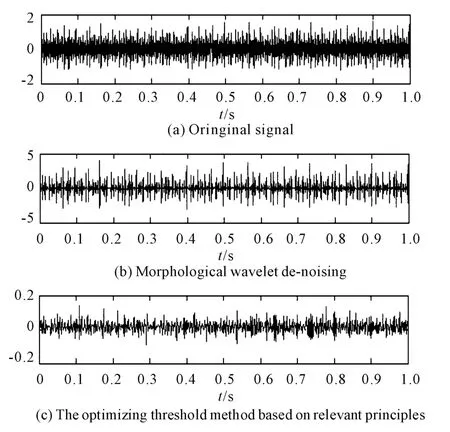
Fig.3 Time domain waveform figure oforiginal signal and de-noise signal

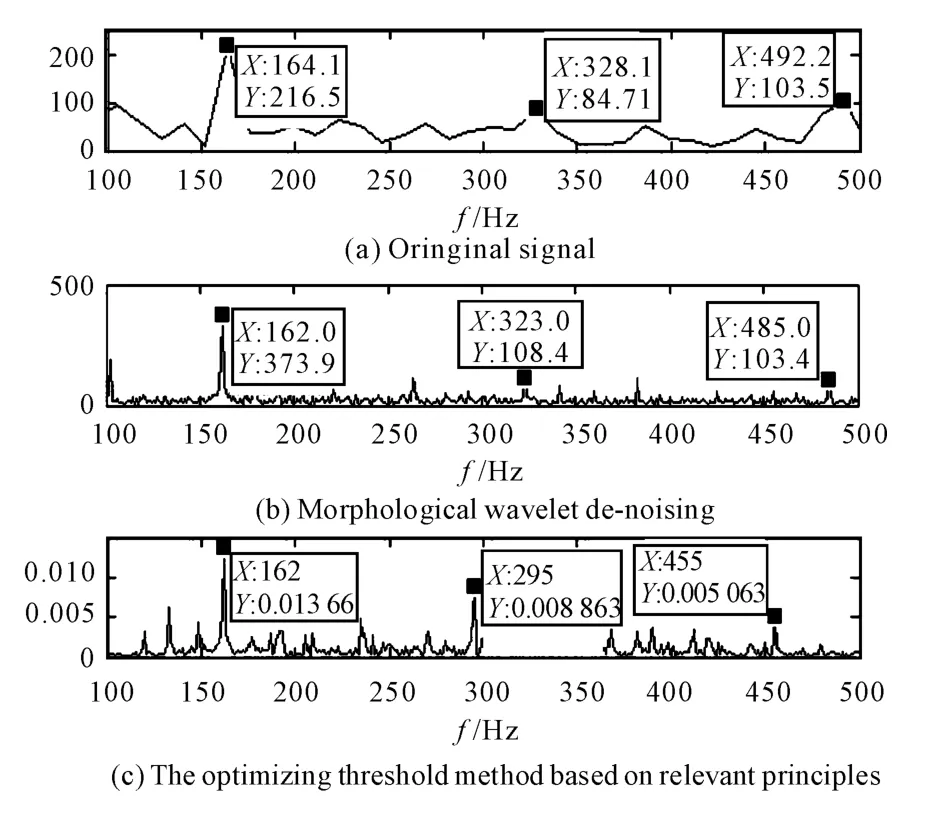
Fig.4 Fault feature extraction

After observing the signal spectrum obtained by various de-noisingmethods in figure 4，we found that it has been decomposed and extracted by the method of morphological median wavelet，peak points in the figure were162 Hz，324 Hz and 483 Hz，since the latter two frequency components is substantially an integer multiple of 162 Hz，belong to the double frequency component.There is sufficient reason to believe that the fault feature frequency of the signal extracted by the method of morphological wavelet is 162 Hz.This is consistent with the theoretical value of the bearing inner ring fault feature frequency we calculat-ed above，which can determine the inner ring race failure.The partially enlarged spectrum after processing by the optimized threshold method based on relevant principles in figure 4 shows that the peak value in 162 Hz，295 Hz and 455 Hz were very prominent，those two peaks behind can be basically considered the double frequency component of 162 Hz，so we can also consider the fault feature frequency extracted by this method is162 Hz，its feature extraction is also relatively accurate，but if we compared its multiple frequency components with those extracted by the method of morphological wavelet，we could clearly see that the signal de-noised by the method of morphological wavelet is more accurate.

The peak points extracted by the traditional wavelet de-noising method in the figure were164 Hz，323 Hz and 485 Hz，the feature frequency was 164 Hz，the result is a certain discrepancies compared with the two improved de-noising method，the error is relatively large.We can obviously found that the two improved de-noising method is superiority to the traditional method of wavelet de-noising.And the veracity of the method of morphological wavelet relative to the optimized threshold method based on relevant principles.

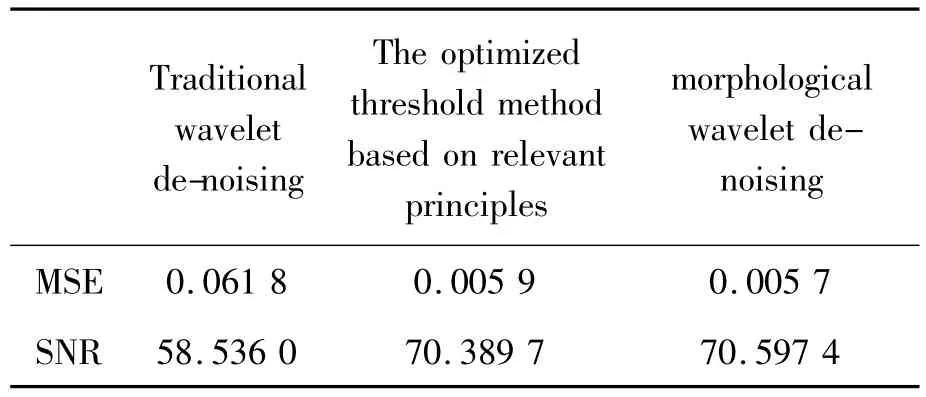
Then let’s analyze the effect of various de-noising methods by MSE and SNR，as shown in Tab.2:

Tab.2 the comparison of mean square error and signal-to-noise ratio

Through the analysis and comparison of MSE and SNR，we can clearly find that the two improved de-noising method can achieve much higher SNR and far lower MSE than the traditional wavelet method，they are able to achieve a better de-noising effect.While through the comparison of two improved methods，we realize that morphological wavelet de-noising method is better than the optimized threshold method based on relevant principles.And in the partial enlarged spectrum graph，we can figuratively see that the feature frequency and the frequency doubling components extracted by the morphological wavelet de-noising method is closer to the theoretical value.

To further compare the pros and cons of the two improved approaches，we compared their program run time using Matlab simulation program.Morphological wavelet de-noising took 2.352 428 seconds to get the result，The optimized threshold method based on relevant principles took 4.834161s to get the result，of course，the run time in different configuration environment will vary，but in the same configuration operating environment，morphological wavelet de-noising is much quicker than the optimized threshold method based on relevant principles，computing efficiency is improved by 51%.

9.Conclusions

1)In the existing improved wavelet de-noising method，the optimized threshold method based on relevant principles can achieve effect far superior to traditional wavelet de-noising method.

2)With the on-linear filtering characteristics of morphological wavelet，applying it to nonlinear timevarying signal processing analysis is feasible.We applied morphological wavelet to the bearing fault signal de-noising and feature extraction in this paper.

3)Analyzing the simulation results，we proved that the diagnostic accuracy and efficiency has been greatly improved by using the method of morphological wavelet de-noising compared with those previous improved threshold methods，we can extract the feature frequency accurately in the early stage of bearing failure，so morphological wavelet de-noising method is a good method for bearing fault diagnosis.It is suitable for on-line fault features analysis.

［1］Donoho D L，LAIN M J.Ideal Spatial Adaptation by Wavelet Shrinkage［J］.Blometrika，1994，81(3)：425-455.

［2］Donoho D L，Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage［J］.Journal of American Statistical Association，1995，90(432)：1200-1224.

［3］Donoho D L.Denoising by soft-threshold［J］.IEEE Trans on Information Theory，1995，41(3)：613-627.

［4］Yuhua Peng.Wavelet transform and engineering application［M］.Beijing：Science Press，1999：1-62.

［5］Ruizhen Zhao，Guoxiang Song.An Improved Method for White Noise Reduction Based on Wavelet Transform［J］.Journal of Univ of science Xidian，2000，27(5)：619-622.

［6］Yanlan He，Yong Su，Yongmei Gao.A Adaptive Wavelet Denoising Algorithm［J］.Actaelectronica Sinica，2000，28(10)：138-140.

［7］Wei Qiang，Chen Xu.A Denoising Algorithm of Wavelet Threshold Based on Translation-invariance［J］.Modern Electronic Technique，2003，149(6)：29-31.

［8］Heijmans H J A M，Goutsias J.Nonlinear Multiresolution Signal Decomposition Schemes—Part I：Morphological Pyramids［J］.IEEE Transactions on Image Processing，2000，9(11)：1862-1876.

［9］Case western reserve university bearing data center［EB/OL］.［2010-01-18］.http：∥www.eecs.cwru.edu/laboratory/bearing/welcome-overview.htm.