秦 蕊

（杭州师范大学理学院，浙江杭州310036）

若环R中元素都为幂等元，即对任意x∈R有x2＝x，则称环R为Boolean环．在1980年，Tominaga将Boolean环推广为广义Boolean环［1］，同时Swaminathan也对Boolean环的另一个推广Boolean－like环作了相关介绍［2］．众所周知，Boolean环是一类特殊的周期环，早在1985年，Abu－khuzam和Ohori等人就对周期环的结构和性质作了相关研究［3－4］．后来，Abu－khuzam的广义J环［5］也为本文提供了重要思想，并且在其近期的Boolean－like环［6］中，对Boolean－like环作了详细说明．在以上基础上，进一步研究Booleanlike环，其主要目的是给出了一种建构广义Boolean－like环的方法，阐述相关的性质及构造若干广义Boolean－like环的例子．文中设N表示所有幂零元素的集合，E表示所有幂等元素的集合．

定义1 环R叫做广义Boolean－like环，如果在R中任取元素a，b都有（a－a2）（b－b2）仍是R中的幂零元．

定义2 设R是交换环，不是零因子，．对加法和乘法定义如下：任取，这样．

s（a1d1－b1c1）＝0，t（a2d2－b2c2）＝0．

引理2 在广义Boolean－like环中任意非零因子都是可逆的．

证明 设x∈R，那么（x－x2）∈N，进而（x－x2）n＝0，因此xn＝xn＋1g（x），g（x）∈Z［x］，这样得到xn（1－xg（x））＝0．因为xn≠0，所以1－xg（x）＝0，故xg（x）＝0．

这就证明了x是可逆的．

定理1 若R是可交换的，Q（R）是一个广义Boolean－like环当且仅当R是广义Boolean－like环．

证明 （⇐）任取x，y∈R，则x（1－x）y（1－y）＝0．由引理2，假设b，d是非零因子，设x＝b－1a，y＝d－1c．取．这样有

b－1a（1－b－1a）d－1c（1－d－1c）＝0．

进而

a（1－b－1a）c1－d－1c＝0．

所以

ab－1（b－a）cd－1（d－c）＝0．

即

也就是

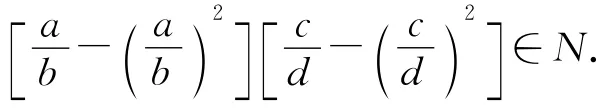
因此Q（R）是一个广义Boolean－like环．

（⇒）任取x，y∈R，则．

R是一个广义Boolean－like环．

定义3 设R是交换环，σ：R→R是一个同构，．那么T是一个环．加法和乘法定义如下：

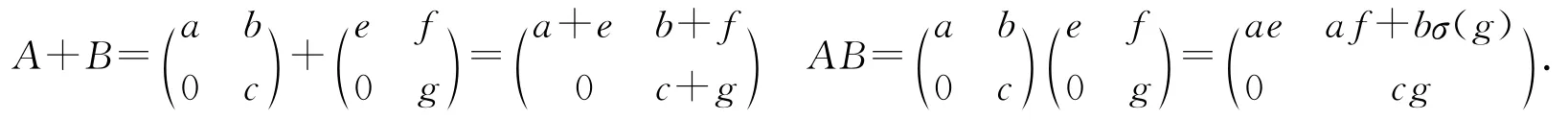
定理2 设R是一个环，σ：R→R为一个同构，且有

那么R是一个广义Boolean－like环当且仅当T是一个广义Boolean－like环．

证明 （⇒）对任意A，B∈T

所以

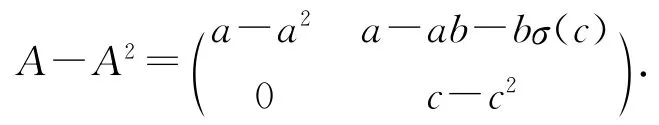
同理

因此

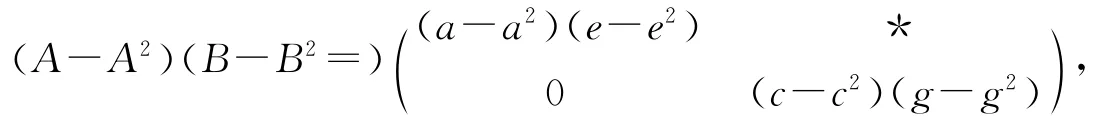
即

［（A－A2）（B－B2）］m＋n＋2＝0，

也就是

（A－A2）（B－B2）∈N．

所以T是一个广义Boolean－like环．

（⇐）任取a，b∈R．令．

容易看到

进而

因此

因为（A－A2）（B－B2）∈N（T），所以（a－a2）（b－b2）∈N（R）．

这样R是一个广义Boolean－like环．

注意1 任意Mn（R）都不是广义Boolean－like环，如

定理3 若R为广义Boolean－like环，那么R中任意元素可以表示为一个幂等元素和一个幂零元素之和．

证明 任取x，y∈R，设x＝y，则

（x－x2）（y－y2）∈N，

那么

（x－x2）2∈N（R），（x－x2）m＝0，

因此

xm＝xm＋1f（x），f（x）∈Z（x）．

设

e＝（xf（x））m＝xmfm（x），

e2＝xmfm（x）xmfm（x）＝xm＋1f（x）xm－1fm（x）fm－1（x）＝xmfm－1（x）xm－1fm（x）＝xmfm（x）＝e．

那么可得到

x＋N＝x2＋N＝（x＋N）2＝（x＋N）m＝xm＋N＝xm＋1f（x）＋N＝（xm＋1＋N）（f（x）＋N）＝xf（x）＋N＝（xf（x）＋N）n＝xmfm（x）＋N＝e＋N．

所以x－e∈N，

故存在w∈N，使得w＝x－e．

也就是x＝e＋w，这里e2＝e，w∈N．

定理4 若R是广义Boolean－like环，N是可交换的．那么R中任意元素可唯一的表示为x＝e＋w这里e2＝e，xe＝ex且w∈N．

证明 假设x＝e＋w＝f＋u这里f2＝f，xf＝fx，u∈N．

xe＝ex，因此ew＝we，那么wx＝x2－ex＝x2－xe＝xw．

由于ef＝（x－w）（x－u）＝x2－xu－wx＋wu

fe＝（x－u）（x－w）＝x2－xu－wx－wu

所以ef＝fe，进而（e－f）3＝e－f，（e－f）4＝（e－f）2，因此（e－f）2∈N．

而e－f＝u－w∈E，即使e－f＝w－u＝0，这样e＝f，w＝u，x表法唯一．

推论 若N是可交换的，那么以下说法是等价的：

（i）R是广义Boolean－like环，

（ii）对任意R中元素x，存在唯一的e，x使得x－e∈N这里e2＝e，ex＝xe．

证明 （⇒）显然．

（⇐）设x，y∈R，由（ii）得到x＝e＋w，y＝f＋u这里e2＝e，f2＝f，w∈N且u∈N．

因此x－x2＝e＋w－e2－ew－we－w2＝w－ew－we－w2∈N．

同理y－y2＝f－fu－uf－u2∈N，

那么（x－x2）（y－y2）∈N，所以R广义Boolean－like环．

定理5 设R是广义Boolean－like环，那么环

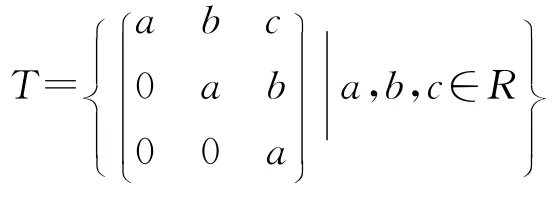
也是广义Boolean－like环．

证明 对任意的

可以看到

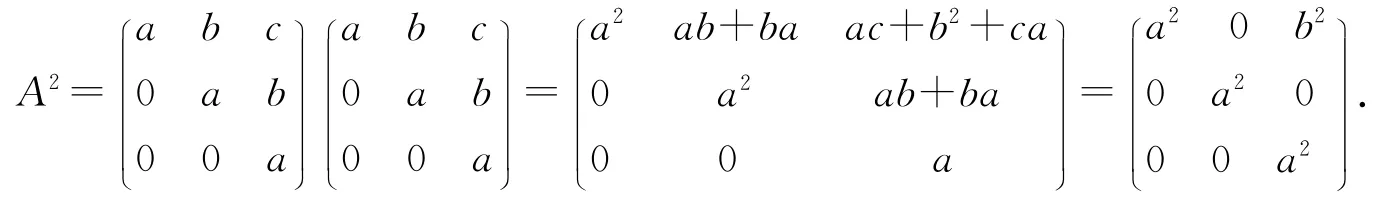
因此

这样

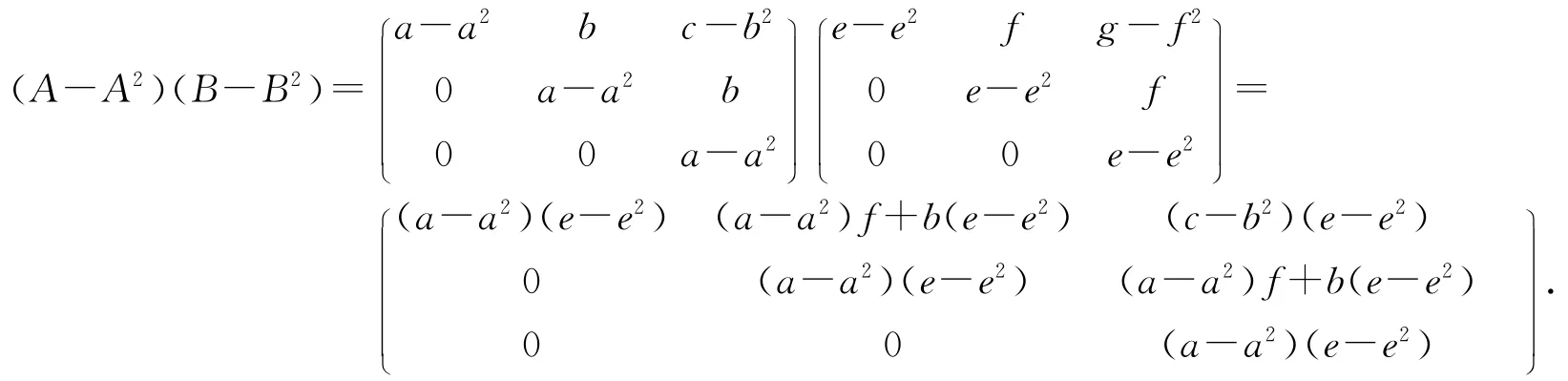
所以［（A－A2）（B－B2）］n＝O，也就是（A－A2）（B－B2）∈N（R）．

那么T是一个广义Boolean－like环．

定理6R是一个广义Boolean－like环当且仅当

证明 取A，B∈T，A＝，

则

所以

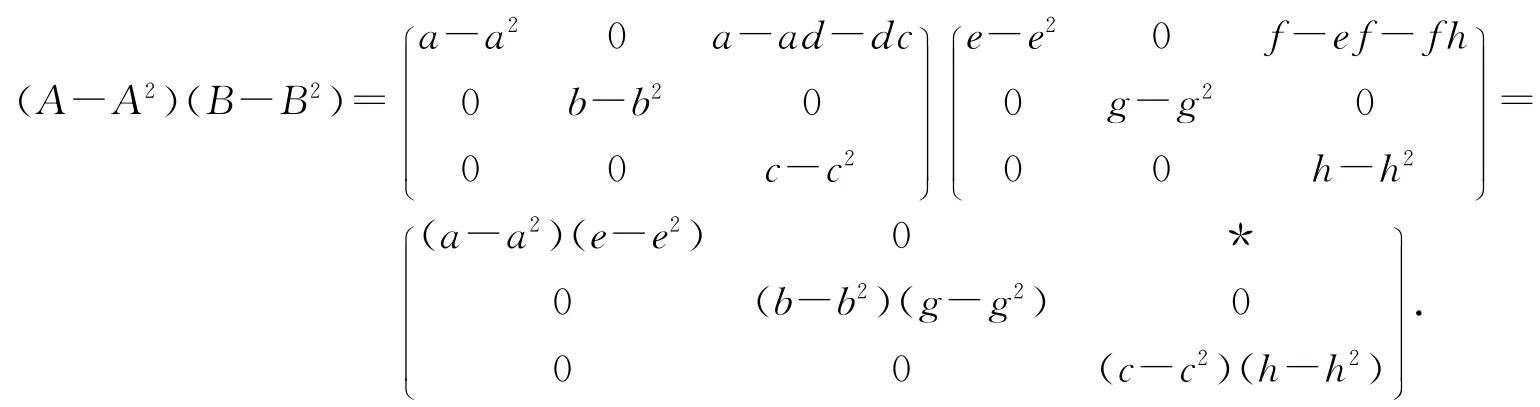
故［（A－A2）（B－B2）］n＝O，（A－A2）（B－B2）∈N（R），

那么S是一个广义Boolean－like环．

反向显然．

注意2 若R是广义Boolean－like环，则eRe也是一个广义Boolean－like环．

显然对任取的eae，ebe∈eRe，由于eRe⊆R，

所以（（eae－（eae）2）（ebe－（ebe）2））n＝0，即eRe是广义Boolean－like环．

注意3 ｛Boolean like环｝⊆｛广义Boolean－like环｝⊆｛周期环｝

（i）广义Boolean－like环不一定是Boolean－like环，由以下例子显然可以得到

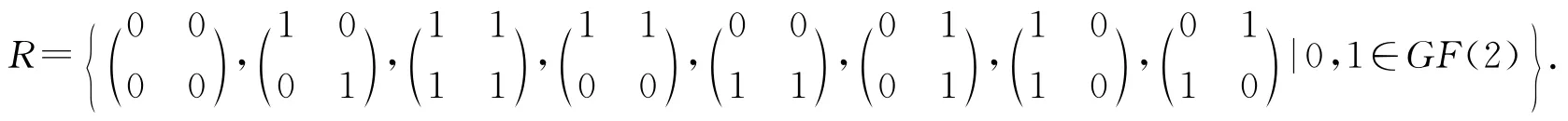
对所有x，y∈R，（x－x2）（y－y2）＝0，因此R是一个广义Boolean－like环．

这样R不可交换，所以R不是Boolean like环．

（ii）周期环不一定是广义Boolean－like环，由下可知

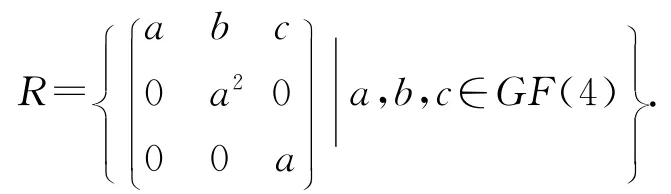
显然它是一个周期环，由于任取x∈GF（4），x4＝x．但是存在a∈GF（4），a2＝1＋a，（a－a2）2＝1，这说明R不是广义Boolean－like环．

［1］Tominaga H，Yaqub A．A Generialization of Boolean Rings［J］．Kyungook Math，1980，12（25）：2．

［2］Swaminathan V．On Foster's Boolean Like Rings［J］．Math Seminar Note，1980，8（2）：347－367．

［3］Abu－khuzam H，Yaqub A．Structure of Certain Periodic Rings［J］．Canad Math Bull，1985，28（1）：120－123．

［4］Ohori M．On Stronglyπ－Regular Rings and Periodic Rings［J］．Math Okayama Univ，1985，7（27）：49－52．

［5］Abu－khuzam H，Yaqub A．Generialized J－Rings and Commutativity［J］．International Journal of Algebra，2008，2（14）：649－657．

［6］Abu－Khuzam H，Yaqub A．Boolean－Like Rings and Related Rings［J］．International Journal of Algebra，2011，5（6）：275－284．