王 莉

（重庆师范大学数学学院，重庆 400047）

随着科学技术的发展，人们发现脉冲微分方程较之不带脉冲的微分方程更能真实地反映自然界发展过程中的某种现象，科学和技术的许多领域如理论物理、机械、种群动力系统、流行病动力系统、工业控制、生物、技术经济等许多方面的变化规律都可以用脉冲微分方程来刻画或描述，这使得脉冲微分方程的研究更有意义.在实际过程中，生态学模型的参数在特定的时间会发生突变，所以本章考虑具有脉冲效应和时变时滞的Hassell-Varley型功能性反应捕食系统，具有一定的生态意义和现实意义.

考虑下面的具有脉冲效应和时变时滞的Hassell-Varley型功能反应的捕食系统：

其中n∈z+，0＜δ＜1，x(t),y(t)表示种群中食饵，捕食者随时间变化过程，k，α，r，β，γ分别表示食饵捕获率，半饱和常数，内禀增长率，捕食者的死亡率和食饵生物量转化为捕食者生物量的转化率；δ称为H-V系数.

t＝tn为定期收获或投放时刻（脉冲时刻），cn，dn分别为食饵，捕食者的收获率或投放率，不失一般生物意义，本章中总是假设：

（i）脉冲时刻｛tn｝,n∈z+满足t0＝0＜t1＜Λ＜tn＜Λ；

（ii）存在正数ω＞0和正整数p，使得tn+p＝tn＋ω, cn+p＝cn, dn+p＝dn,cn,dn＞-1；

（iii）函数 r:R ↦R,k,b ,α,β,γ,τi:R↦ R+是连续ω-周期的（i=1,2,3）.

在（i）-（iii）条件下， R+2是系统(1)的不变集.

为方便，设J⊂R，记 PC ={g:J →R2|g(t)在t≠tk处连续，在t=tk处左连续右极限存在，k ∈ Z+}.

对ω-周期函数g(t)和ω-周期序列｛cn｝｛dn｝，我们采用下列记号：

下面给出本章中需要用到的一些引理：

引理1 （延拓定理[1]）设L是指标为零的Fredholm映射，N在上是L-紧的

假设（a）对任意λ∈(0，1)，方程 Lx=λN x的解满足x∉∂Ω；

（b）对任意的 x ∈∂Ω∩ KerL,QNx ≠0,，而且deg｛ JQ N,Ω ∩KerL,0｝≠0

下面利用重合度理论得到了系统（1）正周期解存在的充分条件.

定理1 如果系统（1）的参数满足：

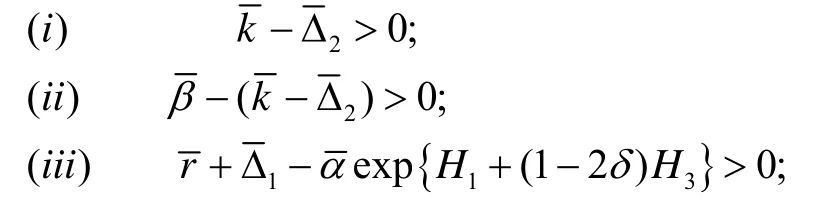
其中

则系统（1）至少存在一个ω-正周期解.

证明：作变换x（t）= exp｛ u（t）｝，y（t）= exp｛v （t）｝，则系统（1）变为

其中

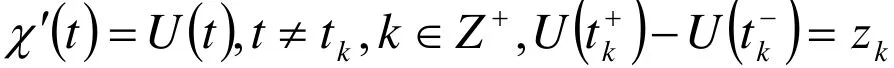
对任意 λ∈ （0,1）由算子方程 LU=λN U，U∈X，有

对（2）从0到ω积分，得

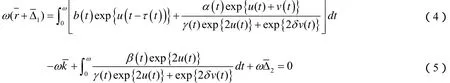
从（3）～（5）知，

由于（u,v）T∈ X ，那么存在 ξi,ηi∈［0,ω ］, i=1,2,使得

由（4）（8）知，

则有

于是，利用（6）（9）有

同样地，由（5）（8）（10）知

则

故而

则

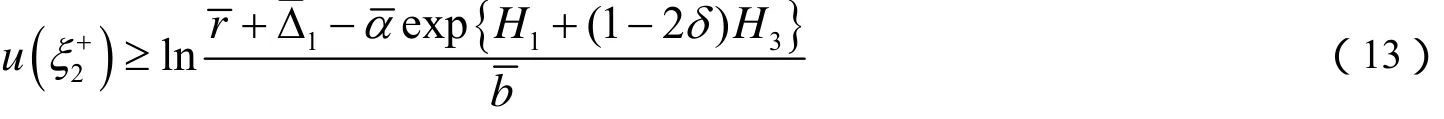
则

则有

则

同样地，由（5）（17）及0 ＜ γ(t) ≤ 1，（γ(t)为食饵生物量转化为捕食者生物量的转化率，故范围在0到1之间）及定理2知，

则

则有

至此，对任意的 λ∈ （0,1），我们已对算子方程 LU=λN U 的解 u（t）,v （t）作了估计：H2≤u（t）≤ H1,H4≤v（t）≤H3,其中 H1,H2,H3,H4与λ无关.

现在我们取

由上估计，对任何 λ∈（0,1）,L U =λNU 的任意解都满足x∉∂Ω，即引理1的第1个条件成立.为验证第2个条件，我们现在考虑关于（u , v ）T∈ R2的代数方程组：

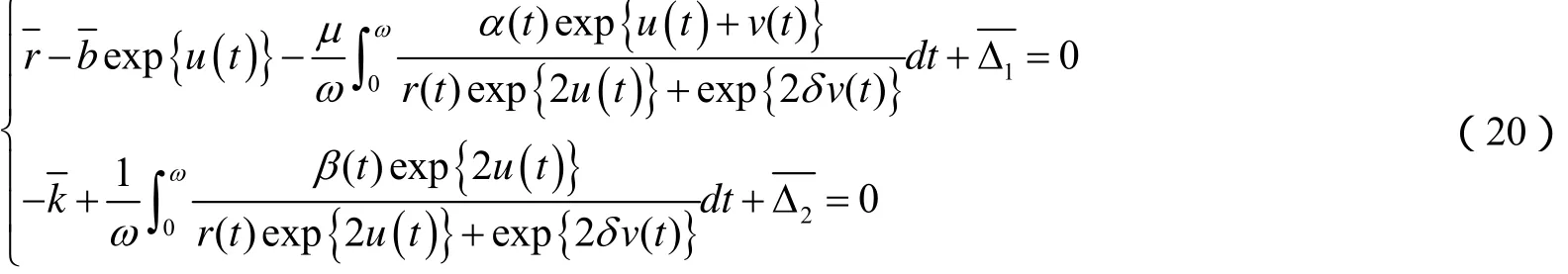
这里μ∈[0,1]，类似以上的估计过程，易证对于任意μ∈[0,1]，代数方程(20)的解（U,V）T有界，事实上，它也满足估计：

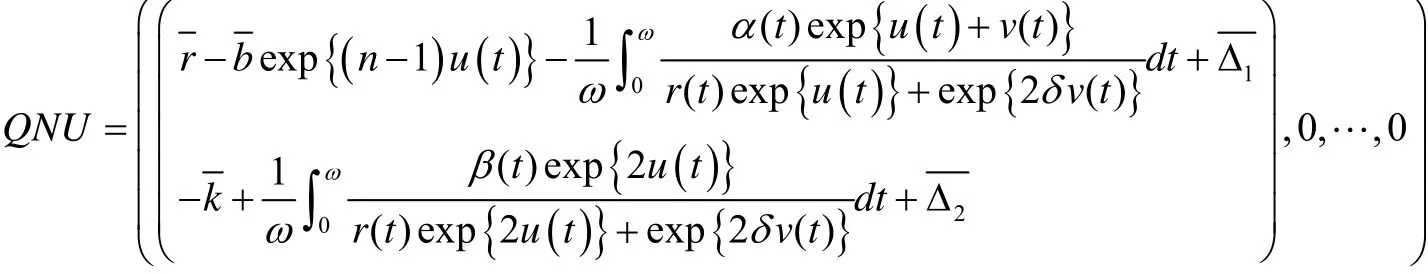
由（9），对任意的 U∈∂Ω∩ KerL,都有 QNU ≠0.为了计算Brouwer度，构造同构变换G（μ,U ）= μQNU+（1-μ）H （U）,μ∈［0,1］.这里， U= （u,t ）T且

从（21）可以看出，对任意 U∈∂Ω∩ KerL 和 μ∈ ［0,1］,都有G（μ,U ）≠0.由假设， H （U）=0都有唯一 解 . 由 Im Q= KerL,取 J=I,并 利 用 同 构 不 变 的 性 质deg ｛JQN ,Ω ∩KerL, 0｝ =deg ｛Q N ,Ω ∩KerL, 0｝ =deg ｛H ,Ω ∩KerL,0｝ ≠0.因此，我们验证了引理1的所有条件.从而 LU= NU在DomL ∩上至少有一解 （U*（t）,V*（t））T，且也是方程（2）的周期解. （x*（ t）,y*（t））T= （exp｛u*（t）｝,exp｛v*（t）｝）T也是方程（1）的正周期解.证毕.

[1] Gaines R.E.and Mawhin J.L.,Coincidence degree and nonlinear differential equations[M].Springer-Verlag,Berlin,1977.

[2] Hassell M P. Varely G C.New inductive population model for insect parasites and its bearing on biological control[J].Nature,1969,223:1133-1137.

[3] Arediti R and Ginzburg L.R.Coupling in predator-prey dynamics:Ratio-dependence,J[J].Theoretical Biology,1989,139:311-326.

[4]温绍雄，范猛.离散Hassell-Varley型功能性反应的捕食者-食饵系统周期解的存在性[J].东北师大学报：自然科学版，2011（1）.

[5]罗廷友，刘启宽，李映辉.一类食饵-捕食系统的定性分析[J].四川理工学院学报：自然科学版，2011（2）.

[6]刘秀湘，黄立宏.离散Hassell-Varley型功能性反应系统的正周期解[J].数学的实践与认识，2009（12）.

[7]杨志春.具有脉冲和Holling III类功能反应的捕食系统的持续生存和周期解[J].生物数学学报，2004（4）.

[8]王守和，李常菊.一种非自治捕食链系统的持久性与全局吸引性[J].三峡大学学报：自然科学版，2009（6）.

[9]杨志春，徐道义.具有反馈控制和无穷分布时滞的脉冲型竞争系统的正周期解及其稳定性[J].应用数学学报，2009（1）.

[10]陈巧灵，栗永安，姜彩玉.具有阶段结构与功能反应的捕食-食饵系统的最优捕获策略[J].重庆工学院学报：自然科学版，2008（11）.

[11]樊晓明，王志刚，罗振江.具功能反应的投放率的非自治捕食-食饵系统的周期解和持久性[J].数学的实践与认识，2008（9）.

[12]范猛，王克.多种群生态竞争系统周期正解的存在性和全局吸引性[J].数学学报，2000（1）.