徐 明

(北京航空航天大学 宇航学院，北京100191)

谭 田 李志武

(航天东方红卫星有限公司 研发中心，北京 100094)

徐世杰

(北京航空航天大学 宇航学院，北京100191)

随着人类空间活动的发展，航天器对轨道机动能力的需求越来越强.以轨道拦截、远程交会等飞行任务为例，往往对机动初始、终止位置以及转移时间有严格约束，即Lambert问题.由于Lam－bert转移不存在解析解［1－2］，众多学者着重利用优化算法进行求解:参考文献［3］首先利用遗传算法得到圆轨道之间的最优转移;参考文献［4］通过改进遗传算法进一步得到Lambert双脉冲转移的最优解.但这些研究成果均建立在各种测量误差已知的假设下;考虑到误差分布的随机性，所得到的最优解并不具有普适性.

事实上，在转移期间施加中途修正，可有效地减少交会的落点偏差:这在地月转移和拉格朗日点转移中已有成功应用［5］.中途修正策略的设计包括修正次数、每次轨控时刻以及修正量;本文基于参考轨迹提出线性和非线性3种策略，并应用Monte－Carlo和遗传算法的联合仿真，得到实现代价函数(落点误差最小)在概率意义下的最优解.

与以往直接求解Lambert问题不同，本文将限制性三体问题中求解周期性特解的微分修正算法［6－8］加以改造，得到 J2－Lambert转移轨道并作为中途修正的参考轨迹.显然，J2－Lambert转移轨道基本消除摄动项的影响，则中途修正仅需要补偿导航误差、初始偏差修正的控制偏差等，无需补偿摄动力等影响.

1 微分修正算法生成J2-Lambert转移轨道

根据r0，rf及Δθ可计算二体Lambert转移轨道［1］.显然，考虑J2摄动后，该变轨策略将造成较大的偏差.本文基于生成Halo轨道［2］和J2不变轨道［3］的微分修正算法，设计 J2－Lambert转移轨道.

Lambert变轨策略给出位置交会的转移轨道，控制量为位置0处的脉冲速度增量Δθ;微分修正算法将改进ΔV及转移时间Δt=tf－t0，以实现位置f处的交会.Lambert轨道转移见图1.

图1 Lambert轨道转移

贴近真值的迭代初值，可以保证微分修正算法迭代过程的收敛.由于J2摄动的数量级仅为10－3m/s2，故本文 ΔV的初值取自二体 Lambert变轨策略;为了将探测器导引到目标位置，每次迭代过程都将轨道积分至Rf处，且与Rf具有相同的x(或y，z)坐标分量，而tf即取为该轨道积分时间.显然，0处轨道速度V0的变化ΔV将导致轨道积分时间tf的变化Δtf.

考查第m次迭代，对转移末端f处的位置矢量作一阶Taylor展开，可得

速度修正量ΔV应使得

整理式(1)和式(2)，可得

实际上，微分修正算法可推广到更高阶引力场模型;但考虑到测量和轨控等误差对落点偏差的影响大于非球型摄动高阶项，即J3－/J4－Lambert转移轨道并不能明显改善中途修正的效果;故本文仅利用微分修正算法消除主摄动(J2)项引起的落点偏差.

2 转移轨道的线性化

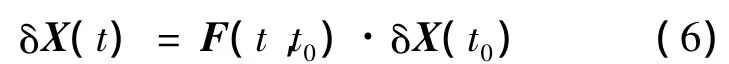
其中，单值矩阵定义为

可通过求解矩阵微分方程得到:

单值矩阵具有如下性质:

3 中途修正策略设计

3.1 基于参考轨迹的线性修正策略I

设Lambert转移过程中进行k次修正.根据修正次数，整个名义轨道被划分为k+1段，如图2所示.

图2 Lambert转移中的中途修正

速度增量ΔVm由于修正轨道，以实现探测器在时刻到达目标位置故由式(10)可解得

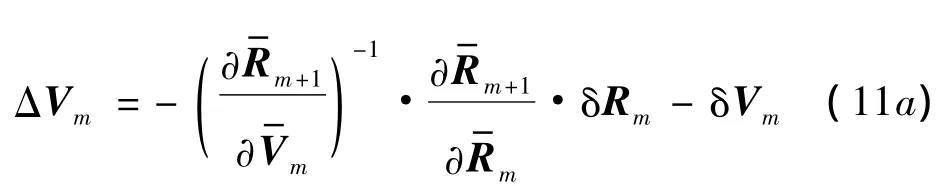
该变种可以看作有k个独立的修正策略Ⅰ组成，且每个策略仅进行一次修正.

3.2 基于参考轨迹的线性修正策略Ⅱ

为了解决以上问题，本文拟采用随机最优控制理论设计修正策略Ⅱ.

为了方便表示，将δX记为Y，将 F(tm+1，tm)简记为F(m+1，m).则探测器运动状态的一阶近似由以下线性差分方程表示:

式中，D(m)=F(m+1，m)·［03×3I3×3］T;白噪声向量W∈N(0，G)和N∈N(0，Q)分别来源于系统未建模误差及每次修正引入的误差和测量误差.

交会(或拦截)位置精度与燃料消耗的加权关系，由二次型代价函数F0确定，其定义为

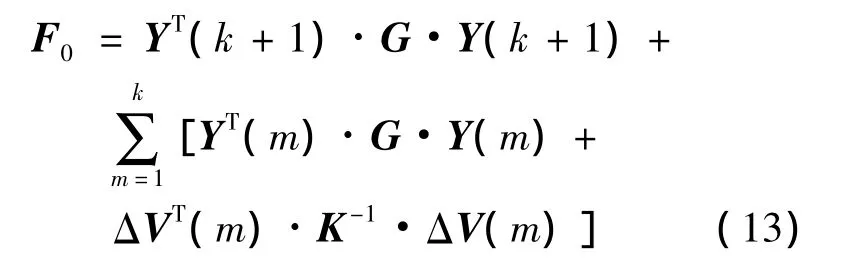
对于该最优问题式(12)～式(13)，可以按照不完全状态信息情形下离散随机最优控制的动态规划法［5，9］求解.求解过程分为以下 3 步:

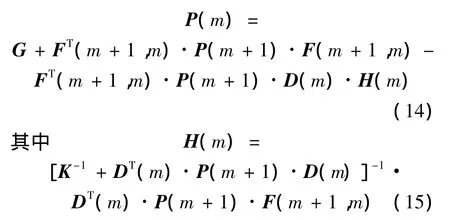
称为Kalman增益.

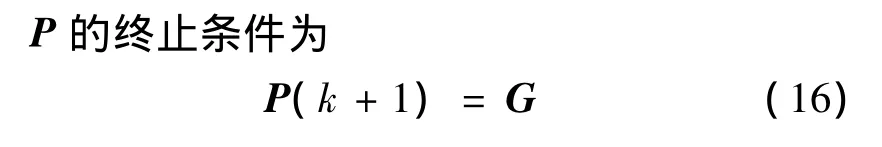
线性最优滤波器:

从而最优速度修正为

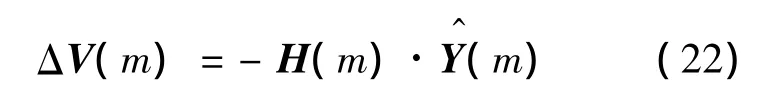
3.3 策略Ⅰ和Ⅱ的关系

不考虑燃料代价，则代价函数F0中加权矩阵取 GR=I3×3，K→∞，即 K－1=0.通过求解 Riccati方程及Kalman增益，可得

式(23)表明，策略Ⅰ本质上是策略Ⅱ的特殊形式.

3.4 基于Lambert迭代的非线性修正策略Ⅲ

微分修正即可设计参考轨迹，还可设计修正策略.整个Lambert转移过程依次在…，k时刻进行k次修正;对于任意修正点，探测器的状态记为和，完成该转移的剩余时间为则根据第1节发展的“J2－Lambert转移轨道的微分修正生成算法”，可以解算出转移到期望终端状态Rf和Vf的修正脉冲ΔVm.

显然，策略Ⅲ独立于名义轨道，具有更强的鲁棒性;策略Ⅰ(特别是其变种)，仅是策略Ⅲ的一阶近似，故策略Ⅲ具有更高精度.策略Ⅰ和Ⅱ仅需进行线性运算，且反馈矩阵经离线设计并装订在星上处理器以减少计算量;相反地，策略Ⅲ需要进行非线性的迭代运算，这将耗费相当的计算资源.

4 最优修正时刻选择

完整的修正策略应包括修正量输出和修正时刻确定.对于给定修正量输出策略，希望设计合适的修正点，以实现代价函数在概率意义下的最优.

而修正时刻的确定，需要针对具有不同统计特性的误差散布来源，对整个随机过程建立复杂的统计学模型;且中途修正不同于连续控制:对于整个动力系统的演化过程，仅需有限次的不连续控制.因此，很难给出概率意义下最优修正时刻的解析形式，本文将基于Monte－Carlo和遗传算法的联合仿真给出数值求解方法.

记εi为最后落点误差，其中i=90% ～99%，表示该误差的置信水平.则对于任意的修正时刻τ，存在映射 Θ:τ→εi(τ).显然，映射 Θ 存在于统计学意义，并且可由Monte－Carlo仿真得到确定.

本文期望找到合适的τ，以使得εi达到最小值.因此，最优修正时刻的选择转化为映射Θ的最优化计算;而工程上，置信水平一般取为90%，95%，99%，即该问题本质上是多目标优化问题.幸运地是，遗传算法的计算结果表明:该多目标最优化模型的Pareto最优解为同一结果，即存在多目标优化最优解.

为了优化算法的实现，需对优化变量修正时刻τ作必要的离散化处理:对整个转移时间Δt=tf－ t0等间隔离散为 N 段，即└t0，t1，…，tN－1，tf┘;并离线计算出各子区间的单值矩阵F(tm+1，tm)，m=0，1，…，N －1，用于构造修正策略Ⅰ或Ⅱ.

5 仿真算例

根据表1的轨道根数确定Lambert转移轨道，如图3所示;整个转移时间Δt=9 000 s.在J2项摄动的影响下，该转移轨道将有65.09 km的落点偏差;在21×21阶引力摄动下，落点偏差将达到65.134 km;经过“生成 J2－Lambert转移轨道的微分修正算法”矫正后，该转移轨道在21×21阶引力摄动下偏差仅为35.9243 m.

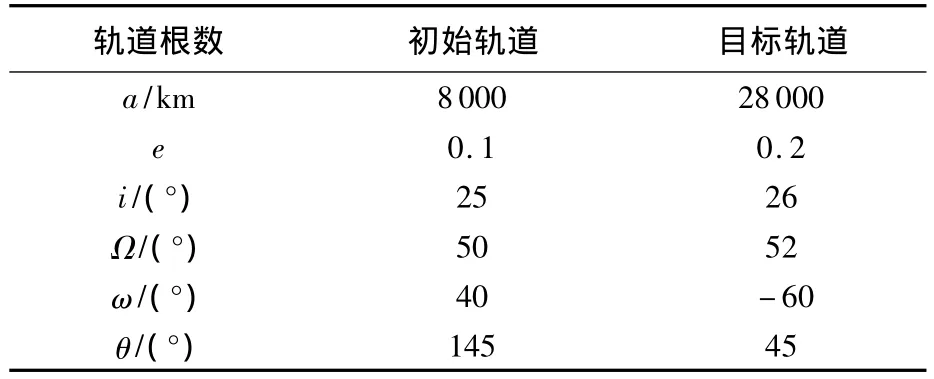
表1 初始轨道和目标瞬时轨道根数

由于存在导航误差E1和转移轨道的初始偏差E2以及Lambert脉冲速度偏差E3，将会造成探测器真实飞行轨道偏离名义轨道，故中途修正是必要的;而中途修正将会引入修正速度偏差E4.

以下误差源认为服从Gauss分布，均值都为零，方差各为:E1和E2的位置偏差200 m，速度偏差0.01m/s(1σ);E3和E4的速度大小偏差0.1%，速度在径向方向偏差0.573°(3σ).而速度法平面内的偏差满足［0，2π］上的均匀分布.

本文采用修正策略Ⅰ来制导Lambert转移，并利用“Monte－Carlo和遗传算法的联合仿真”求解最优修正时刻.遗传算法的参数取为:种群数为40，遗传代数为25，选择代沟为0.9，交叉概率为0.7，变异概率为 0.0017;Monte－Carlo 仿真次数为500.优化变量τ的离散间隔N取为300.

优化目标为寻找ε90%，ε95%和ε99%的最小值，而遗传算法的数值结果显示:该多目标最优化模型的Pareto最优解为同一结果，即存在多目标优化最优解 τ*=390 s，对应的落点误差分别为8.82 km(置信度90%)，9.94 km(置信度95%)和10.82 km(置信度99%).最优解的寻优过程见图4，而最优修正策略的落点误差分布见图5.

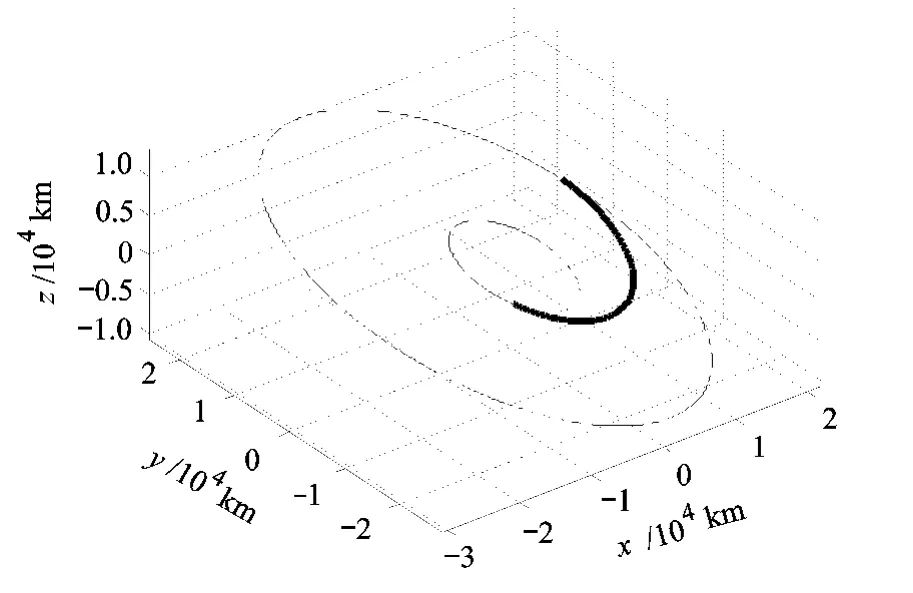
图3 Lambert转移轨道

图4 遗传算法的寻优过程

图5 最优修正策略的落点误差分布

6 结论

本文应用Monte－Carlo法和遗传算法的联合仿真求解Lambert转移中途修正的全局概率最优策略.以往利用优化算法直接求解Lambert问题，需要已知各种测量误差的大小，即所得到的最优解并不具有普适性.为了有效地减小交会的落点偏差，可在转移期间施加中途修正.本文针对转移的最终落点误差，设计3类中途修正策略以适应不同的精度需要.以第Ⅰ类修正策略为例，应用Monte－Carlo和遗传算法的联合仿真，得到在概率意义下的最优修正时刻.

中途修正的参考轨迹设计，基于限制性三体问题中求解周期性特解的微分修正算法构造，以消除摄动项的影响，则中途修正仅需要针对导航误差、初始偏差修正的控制偏差等进行补偿.

本文应通过Monte－Carlo法和遗传算法的联合仿真发现“不同置信水平具有相同的概率最优策略”结论;该结论对于设计工程实用的修正策略具有重要意义，而如何从理论上证明上述结论将是下一步的工作重点.

References)

［1］Battin R H.An introduction to the mathematics and methods of astrodynamics［M］.New York:AIAA Inc，1987

［2］韩潮，谢华伟.空间交会中多圈Lambert变轨算法研究［J］.中国空间科学技术，2004(5):9－14 Han Chao，Xie Huawei.Research on algorithm of loopy Lambert transfer in space rendezvous［J］.Chinese Space Science and Technology，2004(5):9 －14(in Chinese)

［3］Spencer D B，Kim Y H.Optimal spacecraft rendezvous using genetic algorithms［J］.Journal of Spacecraft and Rockets，2002，39(6):859－865

［4］陈统，徐世杰.基于遗传算法的最优 Lambert双脉冲转移［J］.北京航空航天大学学报，2007，33(3):273 －274 Chen Tong，Xu Shijie.Optimal Lambert two－impulse transfer using genetic algorithm［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(3):273 －274(in Chinese)

［5］Xu Ming，Xu Shijie.Trajectory and correction maneuver during the transfer from Earth to Halo orbit［J］.Chinese Journal of Aeronautics，2008，21(3):200 －206

［6］Xu Ming，Xu Shijie.Nonlinear dynamical analysis for displaced orbits above a planet［J］.Celestial Mechanics and Dynamical Astronomy，2008，102(4):327 －353

［7］Xu Ming，Xu Shijie.Structure－preserving stabilization for Hamiltonian system and its applications in solar sail［J］.Journal of Guidance，Control and Dynamics，2009，32(3):997 －1004

［8］Xu Ming，Xu Shijie.J2invariant relative orbits via differential correction algorithm［J］.Acta Mechanica Sinica，2007，23(5):585－595

［9］Noton M.Spacecraft navigation and guidance［M］.London:Springer，1998