甄南南，朱 军，杨文雷

(杭州电子科技大学数学研究所，浙江杭州310018)

0 引言

导子在理论和应用中都是一类非常重要的映射。许多学者都对导子的局部特征做过研究。文献1证明了一阶情况下套代数上全可导点的特征，即G≠0。文献2证明了套代数上在0点可导且满足φ(I)=0的映射是导子。文献3证明了若N是Banach空间上的一个完备套，那么每一个值域在N中的幂等元都是AlgN中的全可导点。文献4证明了CSL代数上在0点可导且满足φ(I)=0的映射是导子。本文将文献1的结论推导到高阶的形式，即G∈AlgQ是高阶全可导点当且仅当G≠0。

1 套代数上高阶全可导点

定理1 设Q是Hilbert空间H上的非平凡完备套，则G∈AlgQ是高阶全可导点当且仅当G≠0。

证明 设dn是从AlgQ到其自身的在G≠0点高阶可导的线性映射。d0为恒等映射。令N∈Q且{0}⊂N⊂H，必有H=N⊕N⊥。0，其中 D∈AlgQN，E∈B(N⊥，N)，F∈AlgQN⊥。λ 默认为是大于0的实数。为了书写方便，把所有的恒等算子都记为I。∀X∈AlgQN，∀Y∈B(N⊥，N)，∀Z∈AlgQN⊥，设 dn(，其中 Aij，Bij，Cij分别是AlgQN，B(N⊥，N)，AlgQN⊥上的线性映射。设 S=，∀X，U∈AlgQN，∀Y，V∈B(N⊥，N)，∀Z，W∈AlgQN⊥满足 XU=D，XV+YW=E，ZW=F，则有 ST=G。由假设知 dn(G)=di(S)dj(T)通过计算可得:

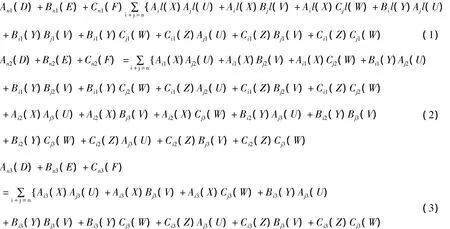
在式1中取X=λ-1XY=λEZ=λFU=λUV=0W=λ-1I，XU=D。两边同乘以λ2并令λ→0;同除以λ2并令λ→∞，由数学归纳法可得Cn1(I)=0和Bn1(E)+Cn1(F)=0。易得An1(D)=Aj1(U)，XU=D。

在式3中取 X=λ-1X，Y=λE，Z=λF，U=λU，V=0，W=λ-1I，XU=D。两边同乘以 λ2并令 λ→0，利用数学归纳法可得An3(X)=0，∀X∈AlgQN。此时式2为:

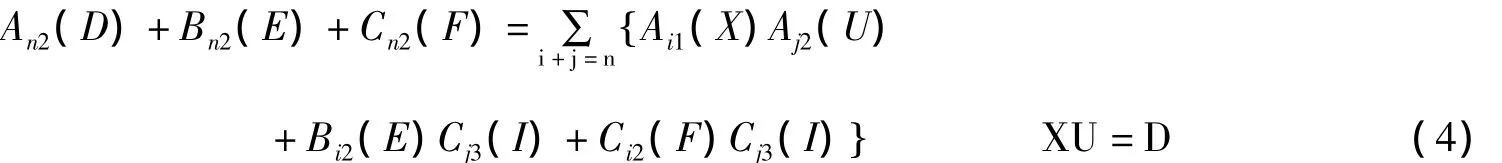
在式1中取 X=λ-1X，Y=λEW-1，Z=λZ，U=λU，V=0，W=λ-1W，其中 XU=D，ZW=F，且 W可逆。两边同乘以λ2并令λ→0，由数学归纳法可得Cn1(W)=0，W可逆。由文献1知∀W∈AlgQN⊥都有Cn1(W)=0。

在式1 中取 X=λ-1I，Y=λ(E-V)，Z=λF，U=λD，V=λV，W=λ-1I。令 λ→0，由数学归纳法可得Bn1(V)=0。在式3 中取 X=λI，Y=Y，Z=-λ-1F，U=λ-1D，V=Y+λ-1E，W=-λI，两边同除 λ并令λ→∞，得=0。由数学归纳法即可得Bn3(Y)=0。

在式3中取 X=I，Y=0，Z=Z，U=D，V=E，W=W，其中 ZW=F，易证 Cn3(·)在 F 点高阶可导。此时式2为:

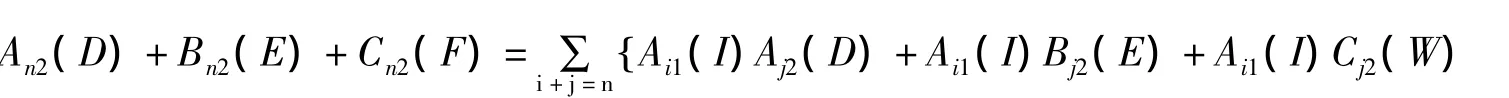
在式2中取 X=I，Y=E-V，Z=F，U=D，V=V，W=I，由数学归纳法可以得到 An1(I)V=VCn3(I)。由前面证明易知Cn3(F)=Ci3(F)Cj3(I)，An1(D)=i+∑j=nAi1(I)Aj1(D)，An2(D)+Bn2(E)+Cn2(F)={ Ai1(I)Aj2(D)+Bi2(E)Cj3(I)+Ci2(F)Cj3(I)}。假设 Cm3(I)=0，Am1(I)=0，0〈m 〈n，即可由数学归纳法得到 FCn3(I)=0，An1(I)D=0，ECn3(I)=0。由文献1知 A11(I)=0，C13(I)=0，联合An1(I)V=V Cn3(I)及G≠0的条件即可利用数学归纳法由文献1中证明得An1(I)=0，Cn3(I)=0，n〉0。此时式4为An2(D)=Ai1(X)Aj2(U)，XU=D。

在式 2 中取 X= λ-1X，Y= λE，Z= λF，U= λU，V=0，W= λ-1I，XU=D。易得{Ai1(X)Cj2(I)+Ai2(X)Cj3(I)}=0。原式化简为An2(X)=-Ai1(X)Cj2(I)。

在式2 中取 X=I，Y=0，Z=λFW-1，U=D，V=E，W=λ-1W，W可逆。易得 Cn2(W)=-Cj3(W)。令W=I代入上式可得Cn2(W)=Ci2(I)Cj3(W)。

在式2 中取 X=X，Y=λEW-1，Z=λFW-1，U=X-1D，V=0，W=λ-1W，X，W可逆。两边同乘以 λ，并令 λ→0，则{ Ai1(X)Cj2(W)+Ai2(X)Cj3(W)}=0，其中X，W可逆。由文献1可知∀X∈AlgQN，∀W∈AlgQN⊥结论成立。此时式5化简为Cn2(F)=Ci2(Z)Cj3(W)，ZW=F。

在式2中取 X=I，Y=Y，Z=FW-1，U=D，V=E-YW，W=W，其中 W可逆，可得 Bn2(YW)=Bi2(Y)Cj3(W)，W可逆。由文献1知∀W∈AlgQN⊥结论成立。则∀W1，W2∈algQN⊥，Bn2(YW1W2)=Bi2(Y)Cj3(W1W2)=Bi2(YW1)Cj3(W2)=Bi2(Y1)Cm3(W1)Ck3(W2)。比较得。在式2中取 X=X，，Y=E-XV，Z=F，U=X-1D，V=V，W=I，类比可得 Bn2(XV)=Ai1(X)Bj2(V)，An1(·)是导子。

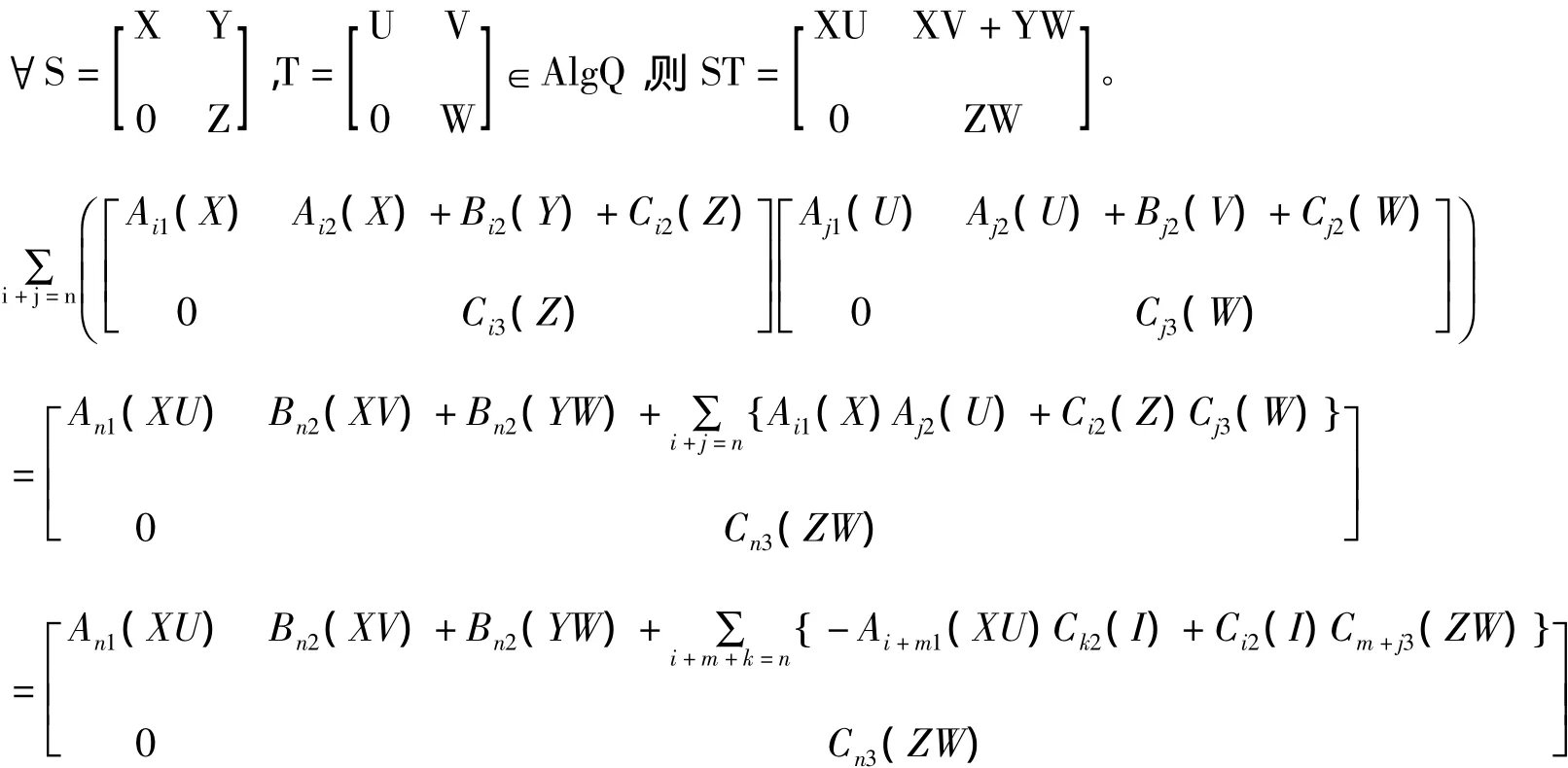
所以dn(·)是导子。

2 结束语

本文在文献1的基础上利用数学归纳法讨论了套代数上高阶全可导点的特征，并给予证明。

［1］ Zhu J，Zhao S.Characterizations of all-derivable points in nest algebras.［EB/OL］.http://arxiv.org/abs/1107.1931v1，2011-07-11.

［2］ JingW，Lu SJ，Li PT.Characterizations of derivations on some operator algebras［J］.Bull Austral Math Soc，2002，66(2):227-232.

［3］ Qi X F，Hou JC.Characterizations of derivations of Banach space nestalgebras:all-derivable point［J］.Linear Algebra Appl，2010，(12):3 183-3 200.

［4］ Li JK，Pan Z D，Xu H S.Characterizations of isomorphisms and derivations of some algebras［J］.Math.Anal.Appl，2007，(2):1 314-1 322.

［5］ Zhu J，Xiong C P，Zhang L.All-derivable points in matrix algebras［J］.Linear Algebra Appl，2009，(8-9):2 070-2 079.

［6］ Gong M，Zhu J.Jordan multiplicative mappings at some points on matrix algebras［J］.Journal of Advanced Research in Pure Mathematics，2010，2(4):84-93.