李泉，高光普，刘文芬

(信息工程大学 信息工程学院，河南 郑州 450002)

1 引言

1999年，密码学者Pieprzyk[1]在研究散列算法的快速实现时提出了旋转对称函数的概念。随着文献[2~6]等对旋转对称函数的进一步分析与研究后，发现这一类结构特殊的布尔函数可以具有良好的密码学性质，并且搜索旋转对称函数要比穷尽搜索布尔函数空间的效率要高，所以一直以来不断地通过改良搜索旋转对称函数空间的方法寻找密码学性质优良的布尔函数。2006年，密码学者Kavut和Yücel[4]利用最速下降法在旋转对称函数空间上搜索到的非线性度为241的9元布尔函数，随后Kavut和Yücel[7]又证明了241为9元旋转对称函数所能达到的最高非线性度。为了得到更好的结果，2008年，Kavut和Yücel[8]推广了旋转对称函数的概念，提出了k-阶旋转对称函数，初步搜索出了9元非线性度为242的3-阶旋转对称函数，并且利用该结论证明了9元、11元、13元非线性度大于的布尔函数都是存在的，彻底解决了这个提出近 30年的公开问题。k-阶旋转对称函数比旋转对称函数对布尔函数代数结构的约束更低，所以数量更多，并且已经寻找到了比旋转对称函数密码学性质更为优良的布尔函数。

本文在Kavut和Yücel的基础上研究了k-阶旋转对称函数的性质。首先，证明了k-阶旋转对称函数的 Walsh谱和自相关函数都满足k-阶的旋转对称。分析发现k-阶旋转对称函数的很多性质都可以利用其轨道来刻画，并给出了k-阶旋转对称函数的轨道中的长圈和短圈的计数公式。特别取 k =1时，利用本文所得计数公式与Sarkar和Maitra所得的计数公式进行比较，发现Sarkar和Maitra所得的计数公式在 n = pa1… pal,l =2且存在 a ≥ 2 ，或 l ≥ 3 的1li情况下是不成立的，并分析了原因。

2 基本概念介绍

记二元域｛0, 1｝为GF(2)，定义GFn(2)到GF(2)上 的 函 数 f(x) = f(x1,x2,… ,xn),x=(x1,x2,… ,xn)∈ G Fn(2)为n元布尔函数。

定义 1[9]n元布尔函数 f (x) ,x∈ G Fn(2)的Walsh谱定义为

定义2[9]设 f (x) ,x∈ G Fn(2)是n元布尔函数，对x = (x,x ,… ,x )∈ GFn(2), s = (s,s , … ,s)∈ GFn(2),12n12n称

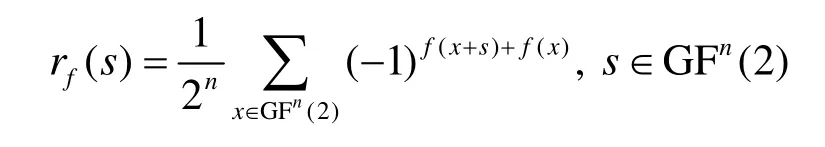
为 f (x)的自相关函数。

n元布尔函数f的自相关函数 rf和 Walsh谱S(f)有如下关系：

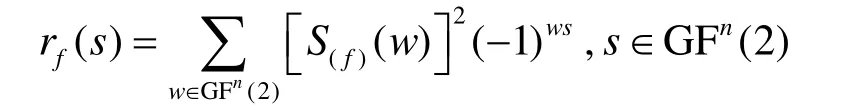
定义3[2]对于任意给定的1≤i≤n,1≤k≤n,xi∈ G F(2)定义

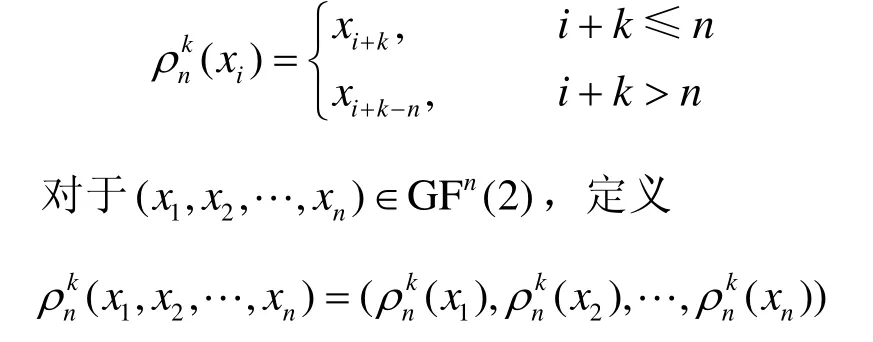
可知， ρnk可视为(x1,x2,… ,xn)的左循环移位算子。

定义 4[8]对于给定的1 ≤ k ≤ n ,k|n ，n元布尔函数f对任意输入的 x = (x,x ,… ,x )∈GFn(2)12n都满足：

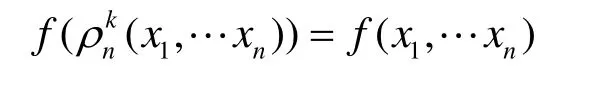
则称 f为k-阶旋转对称函数(k-RSBF)。

注 k =1时f即为旋转对称函数。

定义 5[2]对于给定的1 ≤ k ≤ n ,k|n 和(x1,…xn)∈ G Fn(2)称

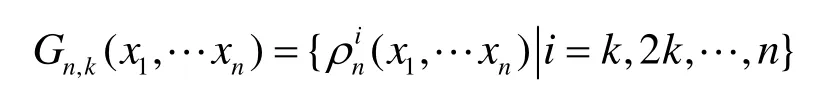
为k-阶旋转对称函数的轨道，简称为轨道。

由定义4可知，对任意的轨道 Gj，k-阶旋转n,k对称函数限制在该轨道上取值为常数。将轨道个数记为将GFn( 2)分成了gn,k个不相交的轨道。显然，中元素的个数且都为的因子，称的轨道为长圈，其个数记为 h ，称n,k的轨道为短圈，其个数记为sn,k。

设 Λ(n,k),j∈ G Fn(2)表示 Gnj,k中元素按字典序排列的第一个元素，称为轨道 Gnj,k的代表元。k-阶旋转对称函数的输出序列可以由长为 gn,k的比特序列

给出，显然该序列包含着k-阶旋转对称函数的全部信息。由该序列可知，变元个数为n的所有k-阶旋转对称函数的个数为 2gn,k。

例1 所有4元2-阶旋转对称函数的轨道为

显然， Gj的全体代表元为4,2

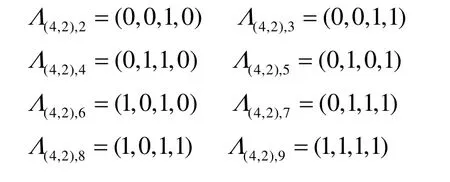
3 k-阶旋转对称函数的性质分析

3.1 k-阶旋转对称函数的 Walsh谱和自相关函数的性质

本节证明了k-阶旋转对称函数的Walsh谱和自相关函数满足k-阶旋转对称。

引理1[3]对任意给定1≤k≤n、w∈GFn(2)和 x ∈ G Fn(2)都有

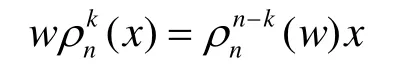
定理1 假设1 ≤ k ≤ n ,k|n 。则布尔函数f是n元k-阶旋转对称函数的充要条件是其 Walsh谱S(f)(w )满足：

证明 1) 必要性。因为布尔函数 f是k-阶旋转 对 称 函 数 ， 则 对 于 给 定 的1 ≤ k ≤ n ,k|n 有f( ρk( x) ) = f(x)，则n

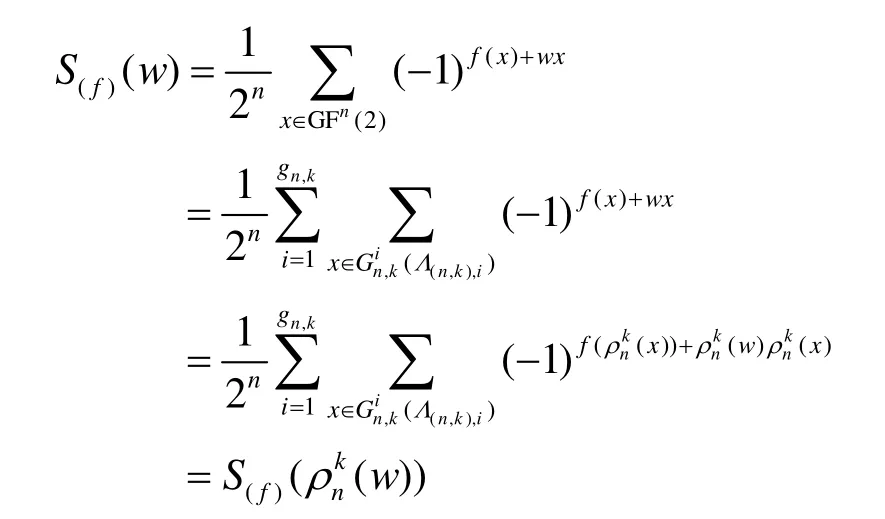
故必要性成立。

2) 充分性。假设布尔函数 f的Walsh谱 S(f)(w)对 任 意 给 定 的1 ≤ k ≤ n ,k|n , x∈ G Fn(2)和w∈ G Fn(2)满足,由引理1可知

由反演公式知

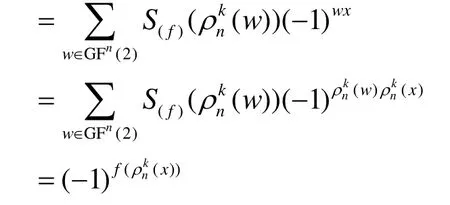
综合1)、2)可知定理1成立。

定理 1说明n元k-阶旋转对称函数 Walsh谱S(f)(w )的取值个数不超过 gn,k个，约是n元旋转对称函数Walsh谱取值个数的k倍。所以它可以具有比n元旋转对称函数更为均匀的谱值分布，即更高的非线性度。

定理2 假设1≤k≤n,k|n，布尔函数f是n元k-阶旋转对称函数，则其自相关函数 rf(s)满足

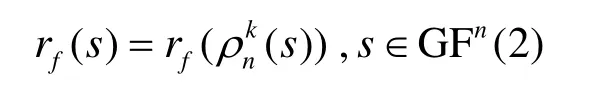
证明 由布尔函数Walsh谱和自相关函数的关系可知

又由定理1的结论知

定理2的逆命题是不成立的（Bent函数的自相关函数在所有非零点都是零，但Bent函数显然不全是k-阶旋转对称函数）。所以定理2不能作为k-阶旋转对称函数的等价判别条件。

3.2 k-阶旋转对称函数轨道中的长圈与短圈计数

由前述可知，k-阶旋转对称函数的输出序列、Walsh谱和自相关函数等都可以通过其轨道进行分类，所以有关k-阶旋转对称函数的轨道的计数和性质的研究是有意义的。本节利用组合论的知识分别给出了k-阶旋转对称函数的轨道中的长圈和短圈的计数公式。首先介绍几个基本概念。

引理2[2](Burnside引理) 假设G为一个作用在集合S上的置换群，则G作用在S上得到的轨道数量为，其中

引理 3[10](容斥原理) 设 A1, A2,… ,An是有限集合，则

文献[8]根据g 引理2给出了下面结论。

定理3[8]n,k表示n元k-阶旋转对称函数的轨道的个数，则，φ(t)为欧拉函数

表1给出当 n = 4 ,6,… ,1 5时， gn,k的取值。

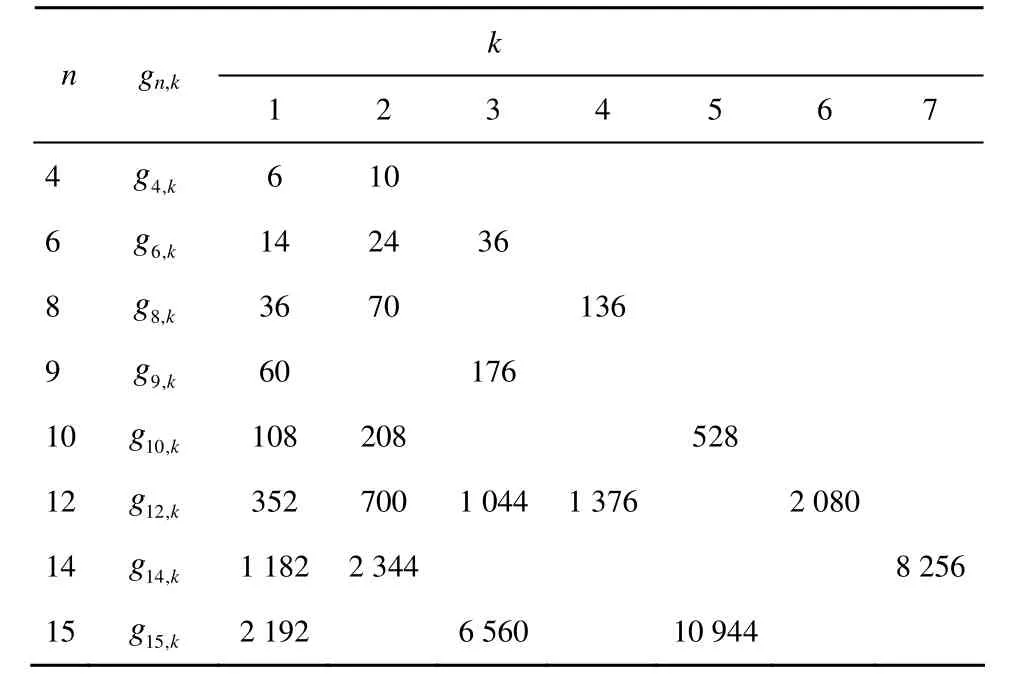
表1 n=4,6,…,15时gn,k的取值

通过表1可以看出，k-阶旋转对称函数的轨道个数约是旋转对称函数的轨道个数的k倍。

推论1 对于素数p，若 n = pa，显然 k = pb且0≤b≤a，则

证明 因为 n = pa,k =pb，其中，0≤b≤a。则可用 pi,0≤ i≤ a - b表示所有的因子，又因为φ( t ) 为欧拉函数，则由欧拉函数的性质得φ( t) = φ ( pi) = pi- pi-1。由定理1可知：

定理 4 hn,k表示n元k-阶旋转对称函数的轨道所有长圈的个数，则，μ(d)为默比乌斯函数

证 明 首 先 对 于 给 定 的1 ≤ k ≤ n ,k|n ， 令，易知G是循环群，对任意的π∈G，π可以分解成两两不相交且长度相同的轮换之积。令，表示在G作用下由向量x生成的轨道，定义轨道的重量为向量x的汉明重量。

i0或1。因此，。又对任意的⊆ { p1, p2,… pl}，可知 l cm( pj1, pj2,… , pjs)=pj1，所以。由引理3可知：

又因为每个长圈的元素个数都为n个，所以有：

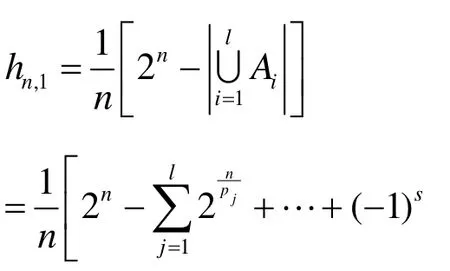
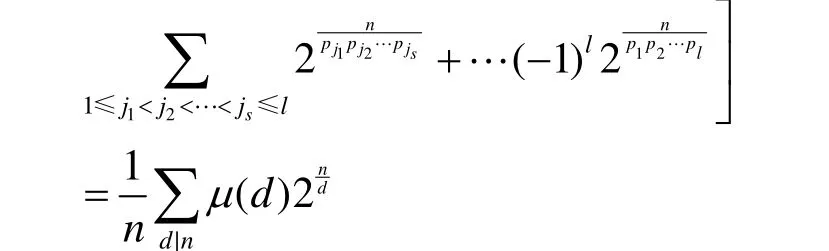
2) 当 k ＞ 1 时 ， 则 G = { ρk,ρ2k,… ,ρmk}。 令nnn。 对 任 意 的 x∈ G Fn(2)， 若，则存在i|m(i＜m)，使得。又因为：

为k个两两不相交的轮换之积，且每个轮换的长度为m。用fix来表示GFn(2)在 G {ρn}下保持不动n的点，由1)的结论可知：

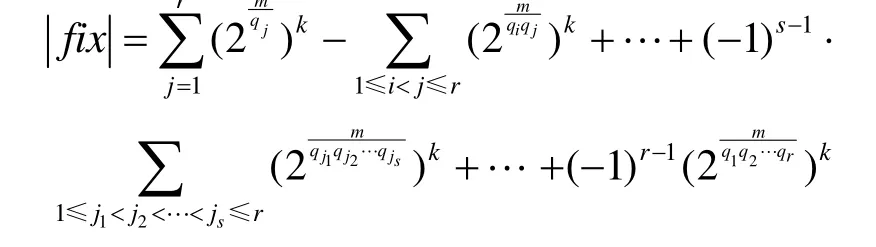
故

综上所述，定理4的结论是成立的。表2给出当 n = 4 ,6,… ,1 5时 hn,k的取值。

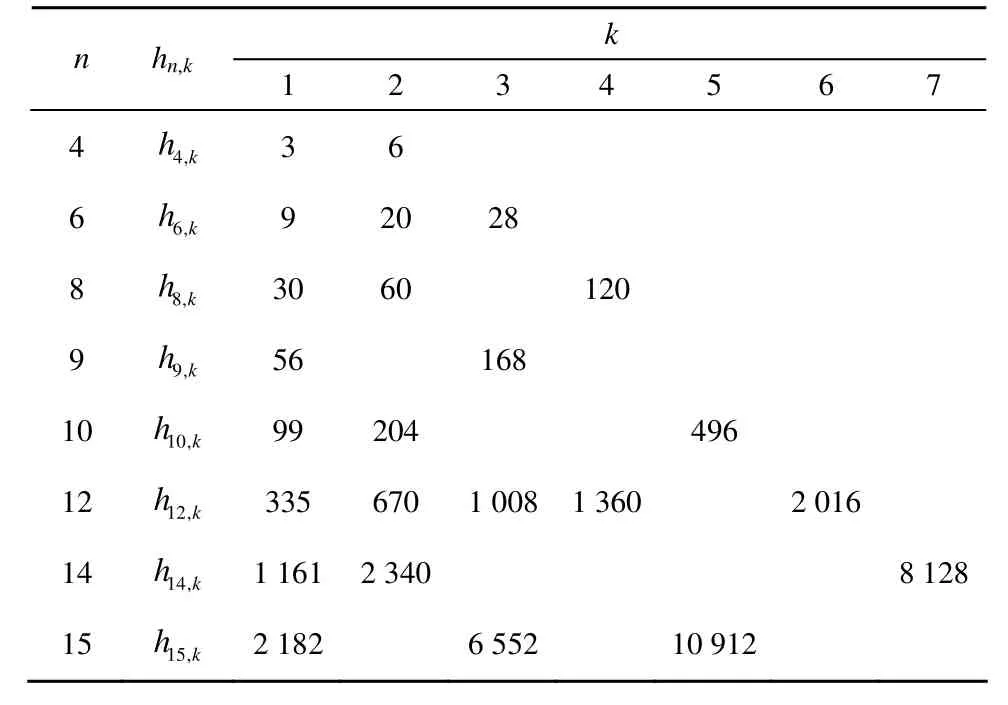
表2 n=4,6,…,15时hn,k的取值

对比表1可以发现，在k-阶旋转对称函数的轨道中长圈占大多数。

推论 2 假设 sn,k表示n元k-阶旋转对称函数的轨道中所有短圈的个数，则

证明 因为 sn,k= gn,k- hn,k, 所以结论是显然的。

前述结论在 k =1时即为旋转对称函数的轨道计数的结论，其相应的结论Sarkar和Maitra在文献[2]中已有详细的描述。值得注意的是，文献[3]所给出的旋转对称函数的轨道中的长圈的计数公式在n = pa1… pal为n的标准分解式时为1l

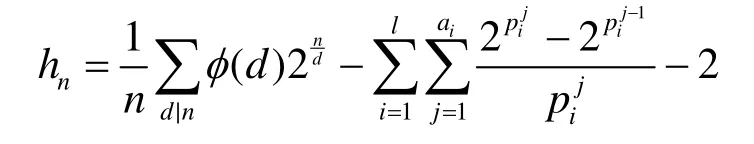
而本文定理4在 k = 1时为

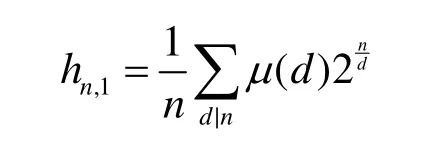
经计算在 n = 1 2 = 22× 3 时文献[2]的结论为h12= 3 44，而定理 4的结论为 h12,1= 3 35。经验证12元旋转对称函数的轨道中长圈个数为335个，说明文献[2]的结论在 n = 1 2时是不成立的。

具体原因是，Sarkar和Maitra得出的n元旋转对称函数的轨道中所有短圈的数量为

之后将轨道总数减所有短圈的数量，所得即为n元旋转对称函数的轨道中所有长圈的数量。但是， sn只计算了所有在和作用下不动的短圈数量，而没有计算所有在 ρnd作用下不动的短圈数量，其中

所以Sarkar和Maitra给出的旋转对称函数轨道中的长圈和短圈的计数公式在 n = pa1… pal,l=2且1l存在 ai≥ 2 (i = 1 ,2)或 l ≥ 3 时都是不正确的。

表3给出当n=1,2,…,30时 hn与 hn,1的取值对比。

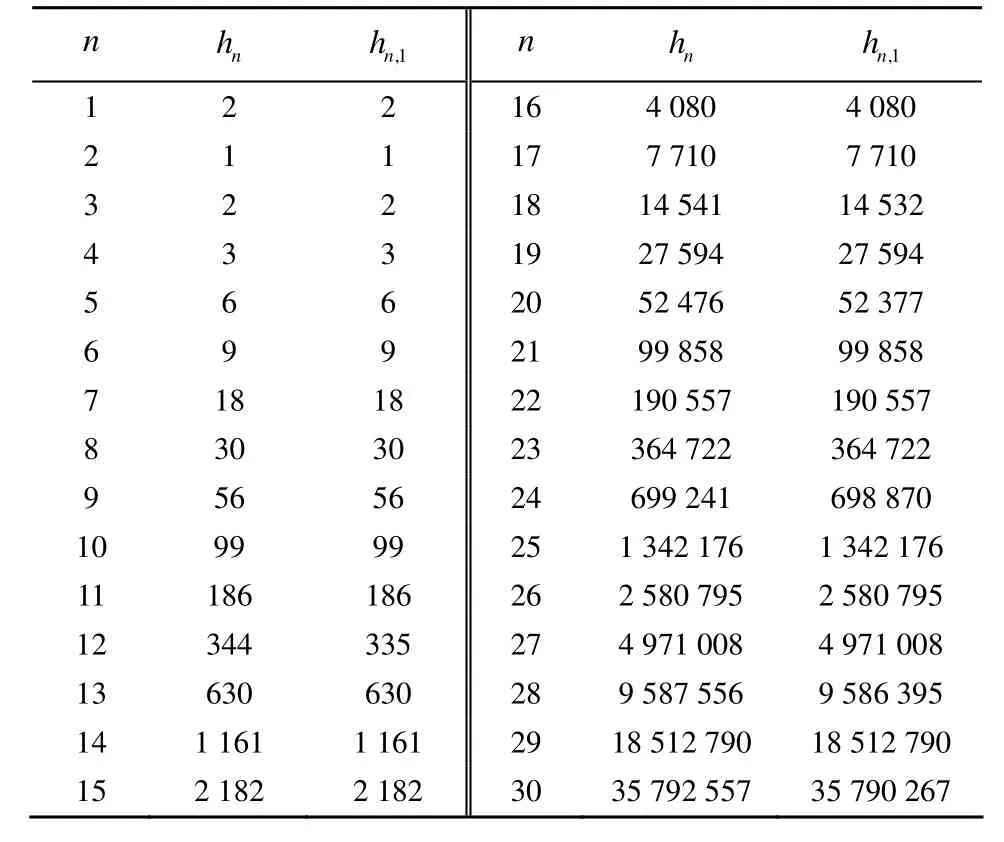
表3 n=1,2,…,30时hn与hn,1的取值对比

通过研究k-阶旋转对称函数的轨道以及轨道中的长圈和短圈的计数，可以了解k-阶旋转对称函数的轨道的性质，从而为更为深入地研究k-阶旋转对称函数的密码学性质提供帮助。

4 结束语

本文分析了k-阶旋转对称函数的性质，证明了k-阶旋转对称函数的 Walsh谱和自相关函数满足k-阶的旋转对称。经分析发现k-阶旋转对称函数的很多性质都可以利用其轨道来刻画，并利用组合论的知识给出了n元k-阶旋转对称函数轨道中的长圈和短圈的计数公式。目前，对于k-阶旋转对称函数的研究工作才刚刚开始，通过深入研究这一类特殊的布尔函数函数从而寻找到密码学性质优良的布尔函数，在理论和实践上都具有重要的意义。

[1] PIEPRZYK J, QU C X. Fast hashing and rotation-symmetric functions[J]. Journal of Universal Computer Science, 1999, 5(1): 20-31.

[2] SARKAR P, MAITRA S. Rotation symmetric Boolean functions-count and cryptographic properties[J]. Discrete Applied Mathematics, 2008,156: 1567-1580.

[3] SARKAR P, MAITRA S, CLARK J. Results on rotation symmetric bent and correlation immune boolean functions[A]. Fast Software EncryptionFSE’ 2004[C]. Berlin, 2004. 161-177.

[4] KAVUT S, YÜCEL M D. Search for boolean functions with excellent profiles in the rotation symmetric class[J]. IEEE Transactions on Information Theory, 2007, IT-53(5): 1743-1751.

[5] MAXIMOV A, HELL M, MAITRA S. Plateaued rotation symmetric boolean functions on odd number of variables[EB/OL]. http://eprint.iacr.org/2004/144.pdf.

[6] MAXIMOV A. Classes of plateaued rotation symmetric Boolean functions under transformation of Walsh spectra[EB/OL]. http:// eprint.iacr.org/2004/354.pdf.

[7] KAVUT S, SARKAR P, MAITRA S, et al. Enumeration of 9-variable rotation symmetric boolean function having nonlinearity>240[A].Cryptology-INDOCRYPT’ 2006[C]. Berlin, 2006.266-279.

[8] KAVUT S, YÜCEL M D. Generalized rotation symmetric and dihedral symmetric Boolean functions-9 variable Boolean functions with nonlinearity 242[EB/OL]. http://eprint.iacr.org/2007/308.pdf.

[9] 李世取, 曾本胜, 刘文芬. 密码学中的逻辑函数[M].北京：北京中软电子出版社，2003.LI S Q,ZENG B S,LIU W F. Logic Functions in Cryptography[M].Beijing: Zhongruan Electric Publishing Company,2003.

[10] 卢开澄, 卢华明. 组合数学（第三版）[M]. 北京: 清华大学出版社,2002.LU K C,LU H M. Combinatorial Mathematics (Third Edition)[M].Beijing: Tsinghua University Press,2002.