郝娟儿，唐莉萍，曾培峰

（东华大学a.信息科学与技术学院；b.计算机科学与技术学院，上海 201620）

基于曲率和面积的二次误差测度网格简化算法

郝娟儿a，唐莉萍a，曾培峰b

（东华大学a.信息科学与技术学院；b.计算机科学与技术学院，上海 201620）

在经典的二次误差测度（QEM）简化算法基础上，将离散曲率和面积引入到边收缩代价计算中，提出了一种基于离散曲率和面积的二次误差测度网格简化改进算法.该算法既考虑了离散曲面在各顶点附近的弯曲程度，又考虑了曲面的几何形状特征.为保留模型的原始边界特征，规定不对其边界进行简化.试验结果表明，改进算法在网格简化过程中保持了原有算法运行速度快的优点，且简化模型能合理地分配网格，并更好地保持了原始模型的重要特征.

网格简化；边收缩；二次误差测度；离散曲率

目前在计算机图形学和几何造型中，三维物体模型的表面通常以三角网格的形式表示.对于大规模的物体模型，为刻画出物体的表面细节特征，相应的三维模型往往需要数量相当庞大的三角网格构建得到.巨大的数据量给计算机的处理和存储、网络数据传输以及实时显示都会带来很大的困难，因此，有必要对三角网格模型进行简化.

三角网格简化的目的是在保持原始三维模型重要几何特征的前提下，通过一定的规则减少三维物体模型表面的三角网格.现有的网格简化算法［1］有顶点删除算法、顶点聚类算法、重新三角化网格算法、区域合并算法和边收缩算法等.其中，边收缩算法是近年网格简化算法研究中非常重要的一类算法，由 HOPPE［2］首先提出，通过对一个全局能量函数进行优化控制实现简化过程.该算法是一个非线性优化过程，需要的数据量大，计算过于复杂，运行速度慢.1997年，GARLAND等［3］提出了二次误差测度（quadric error metrics，QEM）算法，其以新顶点到与被收缩边的两个顶点相关联的平面的距离平方和作为误差测度，用局部二次误差测度计算边收缩代价，这种方法相对简单、运行速度快，且充分考虑了模型的几何相似性，能保持较高的模型整体相似度，但其没有考虑模型的细节特征，产生的简化网格是均匀的，经大规模简化后会出现模型表面的重要几何特征丢失的现象，进而引起细节部分的失真.为保持模型关键特征，文献［4－6］提出采用两个顶点的法向量间夹角判定关键特征，以此提高简化模型的视觉效果.文献［7］通过采用视觉重要度和几何误差建立一个简化代价函数来指导简化，但其数学含义不清晰，实际简化效果无法确定.

本文通过对已有方法的研究和分析，结合模型特征提出一种基于离散曲率和网格面积的QEM改进算法.将三角网格模型顶点的离散曲率引入到二次误差测度的计算中，对曲率变化较大的区域增加误差测度值，推迟其边收缩顺序，在简化过程中使模型的重要几何特征得以保留.同时，将三角网格面积也作为二次误差测度计算的权值，以保证简化生成的新三角网格的质量.

1 QEM算法研究及分析

QEM算法的基本思想是用二次误差测度描述简化误差，通过对模型原始边界内部每个顶点计算相应的误差测度矩阵，得到每条边的边收缩代价，每次简化都选择收缩代价最小的边进行操作，直至达到预期的简化要求.

1.1 边收缩操作

对边 （v1，v2）进行边收缩操作，记为 （v1，v2）→，如图1所示.将一条边（v1，v2）简化为一个顶点，其收缩操作过程如下：

（1）去除原始网格中所有与顶点v1和顶点v2相关联的三角网格；

（2）将顶点v1和v2移至新的位置；

（3）将与顶点v1和v2相关的边和三角网格的信息添加到顶点的信息中.

重复以上边收缩过程，直到简化模型中的三角网格达到预期的数量或一定的简化比例要求.从图1可以看出，一般情况下进行一次边收缩操作可以减少1个顶点、2个三角形和3条边.

图1 边收缩操作Fig.1 Edge collapse

1.2 二次误差测度

模型简化的重点在于选取合适的边进行收缩，使得边收缩最小程度地影响模型的视觉效果.一条边的收缩与否是通过评价这条边收缩后对模型所带来的误差的大小，即收缩代价决定的.每次收缩都选取收缩代价最小的边操作，这样得到的简化模型与原始模型的误差最小.

文献［3］算法在将三角网格中的两个顶点收缩为一个新顶点时，首先计算它的二次误差测度，即计算该顶点到与原始网格中被收缩的两个顶点相关联的三角网格间距离的平方和，并据此求解方程得到新顶点的坐标位置.

三维空间坐标系中的平面可以用方程ax＋by＋cz＋d＝0（a2＋b2＋c2＝1）表示，根据平面方程的系数，可将平面简记为p＝［a，b，c，d］T.设v为网格上的一个顶点，其坐标记为［vxvyvz1］T，P（v）表示与顶点v相关联的三角网格的集合，p为P（v）中的一个三角网格，用p∈P（v）表示.那么，任意一个顶点到三角网格集合P（v）中各三角网格距离的平方之和为

定义顶点v的二次误差测度矩阵［3］为

对于边 （vi，vj）收缩为新顶点，将收缩代价定义为并用Q′i＋Q′j来表示新顶点的二次误差测度矩阵［3］.

2 QEM改进算法

曲率可以描述三角网格模型的重要局部特征.网格模型中的拐点、折痕、尖锐边等关键特征区域内的网格曲率较大，平坦区域曲率较小.因此，本文将曲率引入顶点的二次误差测度矩阵中，进而影响与该顶点相关联的各个边的收缩代价值.在对原始模型进行简化时，本文选择推迟曲率较大区域的收缩顺序，保证边收缩操作主要往曲率较小的方向进行，使得模型的关键特征得以保留.同时将三角网格的面积引入二次误差测度矩阵中，在曲率相同的情况下，优先保留面积较大的顶点，提高三角网格模型质量.这样简化模型能够依照曲率的变化合理地分配网格数量，在弯曲程度较大的区域使网格分布稠密，在平坦区域使网格分布稀疏，可更加有效地保持较多的关键细节特征，在视觉效果上与原始模型相近.

2.1 离散法向量和曲率估计

2.1.1 法向量和曲率

在微分曲面中，曲面的法向量是曲面的一阶微分量，曲面的曲率是曲面的二阶微分量.作为曲面信息的重要度量指标，曲面的法向量和曲率可以量化地表示三角网格模型表面的细节特征信息，如边界、折痕、拐点和尖锐边等弯曲程度较大区域的特征.

三维空间中三角网格模型是由边和顶点相连接而成的分段线性曲面，没有确切的解析表示，无法用传统的曲面解析方法计算.它是一种离散的曲面表示形式，没有连续的法向量和曲率.对于该网格曲面，通常通过计算其顶点处的离散法向量和离散曲率作为曲面在顶点处弯曲程度的近似［8］.

三角网格的数据分析需要存储两种数据结构：一种是顶点数据结构，存储网格中各顶点的坐标；另一种是三角网格数据结构，存储指向组成每个三角网格的顶点数据的顶点索引数据.基于后者可以计算得到离散法向量和曲率.

2.1.2 离散法向量

假设一个三角网格的3个顶点分别为vj－1，v，vj，那么该网格的单位法向量为

遍历三角网格数据结构，用式（3）得到所有三角网格的单位法向量.然后根据各三角网格的单位法向量估算各个顶点的法向量.顶点法向量通过对与该顶点相关联的所有三角网格的法向量进行加权平均得到.考虑与顶点相关联的各个三角网格面积对顶点法向量结果的影响，本文将各三角网格的面积也作为估算顶点法向量时的权值.若一个顶点为v，与它相关联三角网格数量为m，记m为顶点v的维度，则顶点v的单位法向量为

其中：Sj表示第j个三角网格的面积.

这样，可得到三角网格模型中每个顶点的单位法向量，并作为顶点的属性和顶点坐标一起存入三角网格数据结构中.

2.1.3 离散曲率

对于三角网格模型的每个顶点，离散曲面在顶点处沿不同的方向弯曲程度不同.因此，刻画曲面在某一个点附近的弯曲程度，可以用曲面上经过该点的不同曲线的曲率进行评价.

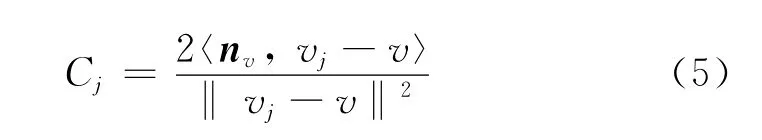
利用式（5）得到和顶点v相邻的各个边方向的离散曲率.根据曲率的大小，可以判断网格模型的关键特征.

2.2 边收缩后的顶点

本文网格简化的基本操作为半边收缩.半边收缩操作不生成新的顶点，收缩后的顶点为原两个顶点中的一个，即简化模型中的顶点是原始模型的一个子集.一条边的两个顶点保留哪个需通过比较这条边两个顶点的收缩代价大小确定.这样既能减少计算新顶点的时间开销，又可以节省存储新顶点的空间开销.

2.3 曲率面积加权误差测度

根据计算得到与每个顶点关联的各边的离散曲率和相邻三角网格的面积，结合QEM算法的原理，求出每个顶点曲率面积加权的二次误差测度矩阵，并用计算得到的边收缩代价指导简化过程中的半边收缩顺序.模型中曲率较大的顶点构成重要特征相关的边，这些边加权之后相应的边收缩代价较大，在边收缩队列中的顺序就靠后.由于推迟了与重要特征相关的三角网格的收缩，模型的重要特征得以保留.

2.4 边界的处理

在原始网格模型内部，由两个顶点组成的边被两个三角面共享.如果网格中一条边只有一个三角面与它相关联，那么这条边就为模型的边界，与它对应的顶点称为边界点.对于有边界的模型，在简化过程应该尽可能保持其边界特征.为保证边界在简化中不被退化，在简化过程中对于原始网格中的边界点应予以保留.在本文算法的程序实现过程中，通过为边界点设置一个非常大的误差测度权值，使边界边的收缩代价处于优先队列的最后，保证不被收缩.这种处理方法简单有效，能够很好保留模型的边界特征.

2.5 改进QEM算法流程

（1）读入初始网格模型的顶点、三角网格数据.

（2）计算网格中每个顶点的离散法向量nv.根据每个顶点的离散法向量，计算出与顶点相邻各边的离散曲率Cj，并结合顶点各相邻三角网格的面积Sj和三角网格对应矩阵Kpj，计算出网格中顶点的二次误差测度矩阵为表述方便，记Sj×Cj，为第i个顶点的权重.

（3）根据网格中各顶点的二次误差测度矩阵，计算每一条边的收缩代价c，并将其放入优先队列中.若 （v1，v2）→，其收缩代价为

（4）从优先队列中取出收缩代价最小的边进行边收缩操作，删除该边及与该边相关的三角网格，更新受影响区域点的邻域，并计算新的边收缩代价，然后更新优先队列.

（5）重复上述过程，直到达到简化要求.

3 试验结果

应用本算法在VC＋＋6.0环境对来源于Internet的三维网格模型进行简化试验，然后将算法得到的简化结果与文献［3］算法结果进行比较.

图2所示为对包含4 952个三角面和2 504个顶点的原始网格模型分别使用文献［3］算法和本文算法，将其简化为仅包含1 000个三角面的简化模型.从图2可以看出，本文算法得到的简化模型，对于额头和脸等平坦区域，使用的三角网格数量相对较少，而对于眼睛、鼻子、嘴巴等细节特征明显的区域，使用的三角网格数量相对较多.

眼睛和嘴部是人体头部模型的最重要特征，图3和4所示分别为将模型简化至2 000个三角网格时，对模型的右眼和嘴部这两个重要特征区域分别采用文献［3］算法和本文算法得到的简化结果.从图3和4可以看出，与文献［3］算法相比，使用本文算法得到的简化模型，在眼角和嘴角这些重要特征区域内，保留更多的三角网格，能更好地保持模型的重要几何特征.

4 结 语

本文在二次误差测度算法的基础上，通过引入离散曲率和三角形面积作为权值计算顶点的二次误差测度矩阵，得到相应的边收缩代价，指导边收缩顺序.算法较好地保持了网格简化过程中原始模型的重要几何特征，使得最终的简化模型能够依照曲率的变化合理地分配网格数量，在弯曲程度较大的区域网格分布稠密，在平坦区域网格分布稀疏，因而有效地保持了较多的模型关键特征，在视觉效果上也与原始模型相近.

［1］HECKBERT P，GARLAND M.Survey of polygonal surface simplification algorithms ［R］. Multiresolution Surface Modeling Course SIGGRAPH'97，PA 15213.Pittsburgh：School of Computer Science，Carnegie Mellon University.1997.

［2］HOPPE H.Progressive meshes［C］//Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques. New Orleans： Association for computing Machinery Press ACM Press，1996：99－108.

［3］GARLAND M，HECKBERT P.Surface simplification using quadric error metrics ［C］//Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques.Los Angeles：Association for computing Machinery Press，1997：209－216.

［4］周石琳，汤晓安，陈敏，等.基于多边形顶点法矢量的网格模型简化算法［J］.中国图象图形学报，2002，7（6）：601－605.

［5］CHEN B，NISHITA T.An efficient mesh simplification method with feature detection for unstructured meshes and web graphics［C］//Proceedings of IEEE Computer Graphics International 2003.Los Alamitos：IEEE Computer Society Press，2003：34－41.

［6］LU G，XU P，WEN X.Triangular mesh simplification algorithm based on vector angle［J］.Journal of Engineering Design，2005，4（2）：124－128.

［7］HUSSAIN M，OKADA Y，NIIJIMA K.Efficient and feature preserving triangular mesh decimation［J］.Journal of WSCG，2004，12（1/2/3）：167－174.

［8］LEE Y，MARSHALL D.Curvature based normalized 3D component facial image recognition using fuzzy integral［J］.Applied Mathematics and Computation，2008，205（2）：815－823.

［9］TAUBIN G.Estimating the tensor of curvature of a surface from a polyhedral approximation［C］//Proceedings of the 5th International Conference on Computer Vision.Los Alamitos：IEEE Computer Society Press，1995：902－907.

A Simplification Algorithm for Curvature and Area－Weighted Quadric Error Metrics Mesh

HAO Juan－era，TANG Li－pinga，ZENG Pei－fengb
（a.College of Information Science and Technology；b.College of Computer Science and Technology，Donghua University，Shanghai 201620，China）

Based on quadric error metrics（QEM），an improved mesh simplification algorithm is proposed.Discrete curvature and triangular area are used in the collapse cost calculation.Both curvature near vertices and surface geometric features are considered in the simplification computation.Meanwhile，edges of the mesh are not collapsed in order to reserve the feature of the object's boundary.The experimental result demonstrates that the proposed algorithm has the same efficiency comparing to the original algorithm，and meshes are distributed evenly in the simplification model，also important features of object are preserved.

mesh simplification；edge collapse；quadric error metrics；discrete curvature

TP 391

A

2011－05－25

郝娟儿（1986—），女，山西运城人，硕士，研究方向为图形与图像处理.E－mail：haojuan108＠126.com

唐莉萍（联系人），女，副教授，E－mail：tanglp419＠gmail.com

1671－0444（2012）03－0318－05