高静华，梁 波

(大连交通大学 理学院，辽宁 大连 116028)

0 引言

微积分中，导数是研究函数性质的核心内容，对于其它导数建立相应的微积分理论也有部分研究，比如本文涉及的对称导数(［1］)，其在文献［2，3，4］中已有部分结果。不同于微积分中的普通导数(参考［5］)，在文献［1］中，介绍了对称导数的定义、运算法则及中值定理。这篇文章里，在［1］的基础上，考虑对称导数的应用价值，探讨其和函数的单调性、极值之间的关系。

为文章完整性，先给出对称导数定义:

定义1(参考［1］) 设函数f是定义在开区间J上的函数，［a，b］是J上的闭子区间，x∈［a，b］。若极限

则称此极限的f在点x的对称导数，记作fs(x)。

从对称导数定义来看，如果一个函数在x点具有经典导数，那么它一定对称可导，并且导函数是相同的，这是因为:

假设函数f(x)在x点具有经典导数，这意味着存在数f'(x)使得

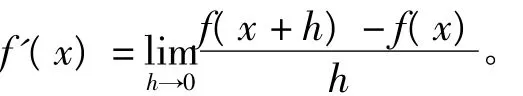
验证极限

上述讨论，简单地说就是可导必对称可导。反之不是不对的，反例可参考文献［1］和［2］。

下面逐一介绍对称导数在函数单调性，极值等问题上的结论。

1 主要结果

定理1(严格单调的充分条件)设函数f在区间［a，b］上连续，fs在开区间(a，b)上存在且∀x∈(a，b)，有fs(x)＞0(fs(x)＜0)，则函数f在区间［a，b］上严格增加(严格减少)。

证明仅证明严格增加的情况，类似的思路可证严格减少的情况。

∀x1x2∈［a，b］，且x1＞x2，由对称导数的广义微分中值定理(定理内容见［1］)，存在y1∈(a，b)，使得

于是，f(x1) ＞f(x2)，即函数f在［a，b］上严格增加。

在数学分析中，通过通常的导数的正负性可判断一些函数的单调性。在这里，通过定理1可以发现，用对称导数的正负性来判断函数的单调性，应用的范围广了很多，这是由于通常的导数比对称导数更强造成的。

通过例1可以知道，f在0点不存在通常的导数，所以无法借助通常的导数来解决此题，但f的对称导数存在，可用定理1来解决这个问题，这是研究对导数的价值和优点所在。以定理1为基础，可获得函数极值的判别法。

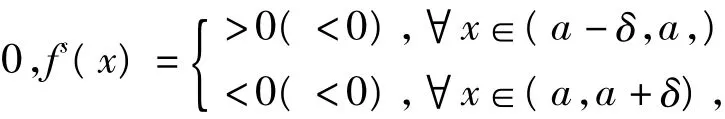
证明仅证极大点的情况，类似方法可证极小点的情况。∀x∈(a-δ，a)，由题设知f在［a-δ，a］上连续，在(a- δ，a)上对称导数存在且fs(x) ＞0，应用定理 1，函数f在(a-δ，a］严格增加，即∀x∈(a-δ，a］，有f(x)≤f(a)。

同理，∀x∈(a，a+δ)，f在［a，a+δ］上连续，在(a，a+ δ)上对称导数存在且fs(x) ＜0，由定理1，函数f在［a，a+δ)严格减少，则∀x∈［a，a+δ)，有f(x)≤f(a)。

于是，∀x∈(a-δ，a+δ)，有f(x)≤f(a)，即a是函数f的极大点，f(a)是极大值。

例2证明0是函数f(x)=|x|的一个极小点。

分析由于f(x)在0点不存在通常的导数，所以不能利用通常的导数来解决这个问题，但f(x)在0点存在对称导数且fs(0)=0，套用定理2的条件可以证得此题，由此也进一步体现了对称导数的优点。

定理3函数f在a的某邻域U(a)存在二阶对称导数，且fs(a)=0，f和fs连续。

1)当fss(x)＞0(∀x∈U(a))时，a是极小点;

2)当fss(x)＜0(∀x∈U(a))时，a是极大点。

证明仅证明情况1)，情况2)类似可证。由题设，∃δ＞0，使得fs在［a-δ，a+δ］⊂U(a)上满足广义微分中值定理(参考［1］)条件，∃x1(a-δ，a+δ)，使得

由定理2知，a是函数f的极小点。

例3证明0 是函数f(x)={x2，x≥0，2x2，x＜0，的极小点。

分析函数f在0点不存在二阶通常的导数，所以不能利用通常的高阶导数办法解决此题，但我们可以利用定理3，因为fs(0)=0且即fss＞0，由定理3得证0是极小点。

关于对称导数的研究不止于此，经典微积分中涉及的有关导数的研究及应用能否延伸到对称导数上来，仍是较为有趣的问题。

［1］汪林.数学分析问题研究与评注［M］.北京:科学出版社，1995.

［2］梁波，王玉斌.对称导数及其相关理论［J］.渤海大学学报，2004，12(4):25-28.

［3］祝英杰，李冠英.二元函数的对称偏导数及其相关理论［J］.长春大学学报，2007(10):20-23.

［4］周相泉，于兴江.对称导数及其性质［J］.聊城师院学报，1994，7(2):17-20.

［5］刘玉琏，傅沛仁.数学分析讲义［M］.北京:高等教育出版社，1992.