易东波，鲍玉昆

(1.华中科技大学管理学院，湖北武汉 430074;2.南昌工程学院工商管理学院，江西南昌 330099)

批量问题在生产库存领域一直备受关注。当需求量因时间不同而有显著差异时，需求时变的批量问题即为动态批量问题，包括确定型时变需求的动态批量问题与随机型时变需求的动态批量问题，其中前者受到更为广泛的研究。解决确定型时变需求动态批量问题的具有开创意义的经典方法则是WAGNER和WHITIN在1958年提出的W-W最优模型及算法［1］。W-W算法引发了大量对确定型时变需求下动态批量问题的研究，相关成果也在库存及生产计划领域得到了诸多应用，有关该类模型和算法种类繁多，具体可参见BRAHIMI等的综述文献［2］。

动态批量中的无能力约束单品种动态批量问题(uncapacitated single item lot sizing problem，USILSP)是研究关注点。USILSP是更复杂的动态批量模型研究的基石，具有重要的基础性研究价值。确定型时变需求的USILSP的相关模型和算法丰富多样，而随机时变需求的USILSP研究相对较少。较早对随机动态批量进行研究的，生产领域有 WHYBARK 和 WILLIAMS［3］，库存领域有SILVER［4］。其后 SOX 和 MUCKSTADT［5］研究了生产排程中随机动态批量的启发式算法，TARIM和KINGSMAN［6］研究了生产库存中带有服务水平约束的随机动态批量问题。WEMMERLOV和WHYBARK［7］分析了在正态分布需求、给定服务水平、无能力约束和不存在缺货回补成本的情形下，各类动态批量算法之间的成本差异情况，而VARGAS［8］给出了正态分布需求下无能力约束的单品种动态批量模型的优化算法。

虽然在假设需求时较多用到正态分布，但现实中很多产品的需求用正态分布不一定就能获得好的拟合。NENES等通过对某企业的调查和研究，发现该企业大多数产品的需求真正为正态分布需求的物品种类较少，而符合Gamma分布的非对称随机需求的物品则占多数［9］，并且，正态分布需求在其变异系数(标准差与均值的比值)非显著小于1时，负需求存在的概率难以忽略［10］，因而可能会在一定程度影响最优策略的适用性。爱尔朗分布作为Gamma分布的典型特例，计算和应用更为简便，亦可用来描述非常规需求的物品，并且如同Gamma分布，不存在负的需求值。当爱尔朗分布在其复合的指数分布的个数较多时，也能逼近正态分布刻画随机需求的效果。因此，应用爱尔朗分布研究需求既可以较好地拟合诸多非常规需求物品，又可避免负需求出现而导致的不利情形，也能在一定条件下做到类似正态分布的效果，从而使相应模型及策略在其应用性方面可能表现得更好。

考虑爱尔朗分布需求下、有缺货回补情形的USILSP，侧重于相应的多时期最优累积批量及动态批量策略的效果，以及其与正态分布情形下的差异性。近来研究随机需求下的USILSP较少，最近的且相关程度较高的研究可详见文献［8］。笔者所用的有关方法与模型借鉴文献［8］进行了爱尔朗分布下的形式拓展，但因该文献并未对其表格“Table A2”中的最优累积批量数据具体如何计算予以说明，笔者对此提出了针对随机动态批量情形的二分搜索算法。二分搜索算法虽在确定型时变需求下的批量决策［11］研究中有应用，但并未应用于随机型时变需求下的批量决策情形中。二分搜索的思想虽简单，但其具体算法及程序并非可以简单移植到不同问题中，且有针对性地提出完整正确的二分搜索算法亦非容易［12］。针对随机动态批量情形的二分搜索算法，经计算验证，该算法是正确可靠的(对文献［8］的表格“Table A1”中的数据结合该二分搜索算法，经计算获得了与“Table A2”中基本一致的数据)。

综上所述，进行该研究的意义有4个方面:一是由于爱尔朗分布较之于正态分布在刻画产品需求方面具有更好的适用性(不存在负需求、能描述更多类别的产品需求)，因而研究爱尔朗分布下的USILSP有助于其相应的研究结论具有更广泛的适用性;二是就目前所了解的相关主流文献而言，还未有专门研究爱尔朗分布需求下的USILSP的文献;三是拓展了二分搜索的应用范围，形成了针对随机时变需求动态批量情形的二分搜索算法，用于动态批量的数值计算中;四是相对于正态分布下的USILSP，该研究提供了在相关数值计算方面可资对照的标杆。

1 相关模型

参照文献［1］和文献［8］关于动态批量模型的假设条件，爱尔朗分布下的动态批量模型亦可具体设定如下:时期为t(1≤t≤T)，需求的概率密度函数为爱尔朗分布gt(x)(x为自变量)，计划期为T期，产能或供应能力不受限制，每期期末确定单位库存持有成本ht或单位缺货惩罚成本bt，且有bt=βht(β为常量)。考虑前置期为L期，t期的固定启动成本为St-L。令rt(x)为gt(x)的相应卷积函数，即有:

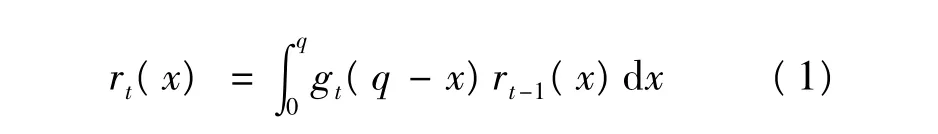
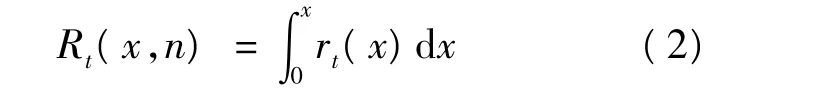
若令 u=λx，则有:

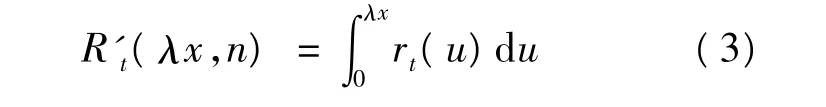
此外，还假定i期(初期)和j期(末期)分别为两个相邻生产批量或补货批量到达的时期，Q为累计批量，Qi，j则为从第i期到第j-1期的累计生产量或补货量，则U(Q，i，j)为从第i期到第 j期(1≤i＜j≤T+1)的期望总成本。若 i=1，j=T+1，则U(Q，i，j)为整个计划期 T期内的总成本。参照文献［8］中的式(3)～式(8)，以及该文献中的有关证明，类似的，相应从第i期到第j期的爱尔郎分布需求下对应的总成本函数表达式式(4)及其最优解的表达式式(5)和式(6)如下:

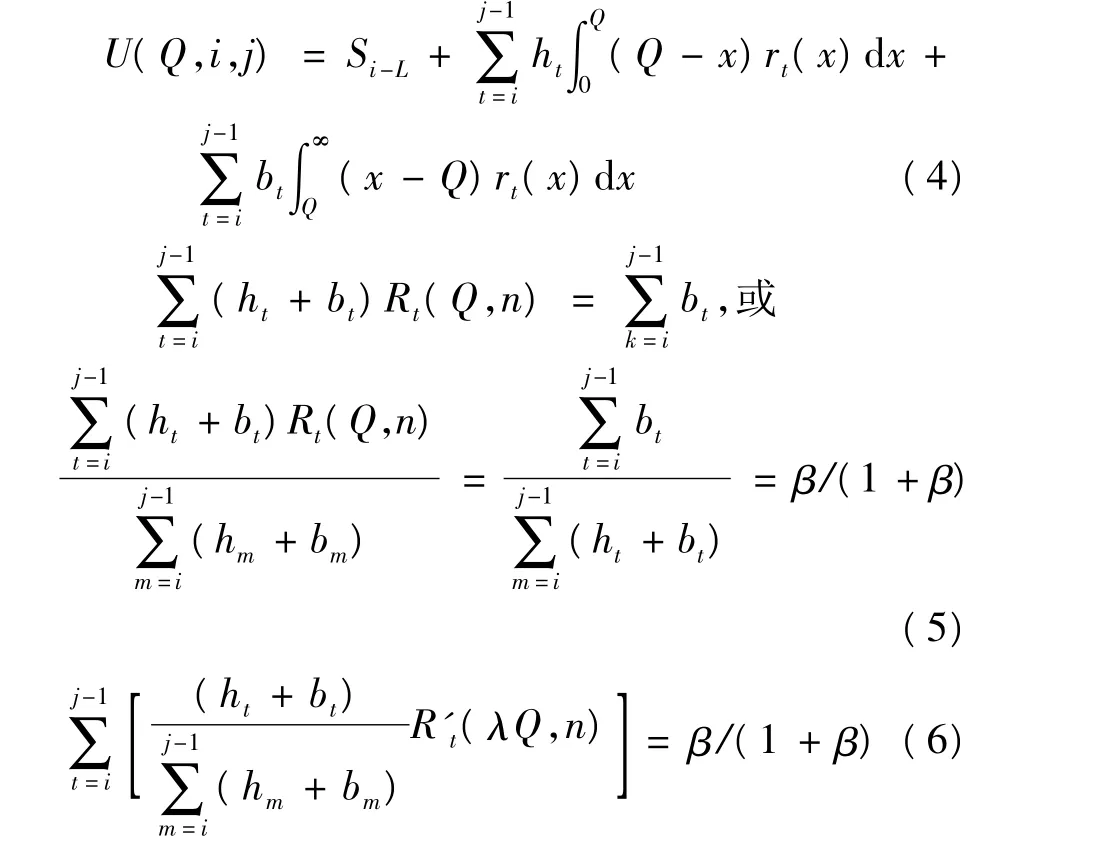
R't(λQ，n)可通过查阅相关概率分布表或通过Matlab软件有关Gamma函数来计算相关数值，例如可计算出从第i期到第j期的最优累计生产批量或补货批量Q*(i，j)。因此，式(4)～式(6)都是可以进行数值计算求最优解的表达式。

2 数值试验及二分搜索算法

为研究在标准差及变异系数均显著变化情况下，爱尔朗分布需求的各最优累积批量与正态分布需求的各最优累积批量之间的差异性，采用两个算例进行数值试验。同时提出了相应的二分搜索算法并编程实现相关计算。

两个算例中的最优累计批量数据按四舍五入取整数，标准差数据按四舍五入取到小数点后1位，相关比值数据按四舍五入取到小数点后两位。第一个算例，采用文献［8］当中的算例数据，其数据亦是在文献［1］数据基础上做了一定的拓展，如在各期单位库存持有成本均为1个单位的基础上，增加了各期单位缺货回补(惩罚)成本均为9个单位;又如，增加了各期需求服从正态分布的假定，将各期需求数据转换为相应的需求均值，并设各期需求标准差为相应需求均值的1/9，即变异系数为1/9。通过算例1的计算，可验证在同等变异系数(标准差均值比为1/9)情况下，各最优累积批量在爱尔朗分布与正态分布下的差异性。第二个算例，则在文献［8］数据的基础上，均值不变的同时，将其各期的标准差数值均增大为原来的约6.4(≈6.4)倍，即变异系数为，以了解相应的差异性发生新变化的情况。

算例1 相关参数分别为:对所有t(1≤t≤T)，ht=1，bt=9，σt/μt=1/9。由于 n=(μ/σ)2，则对于所有t，n=(μ/σ)2=81。具体需求相关数据如表1所示。

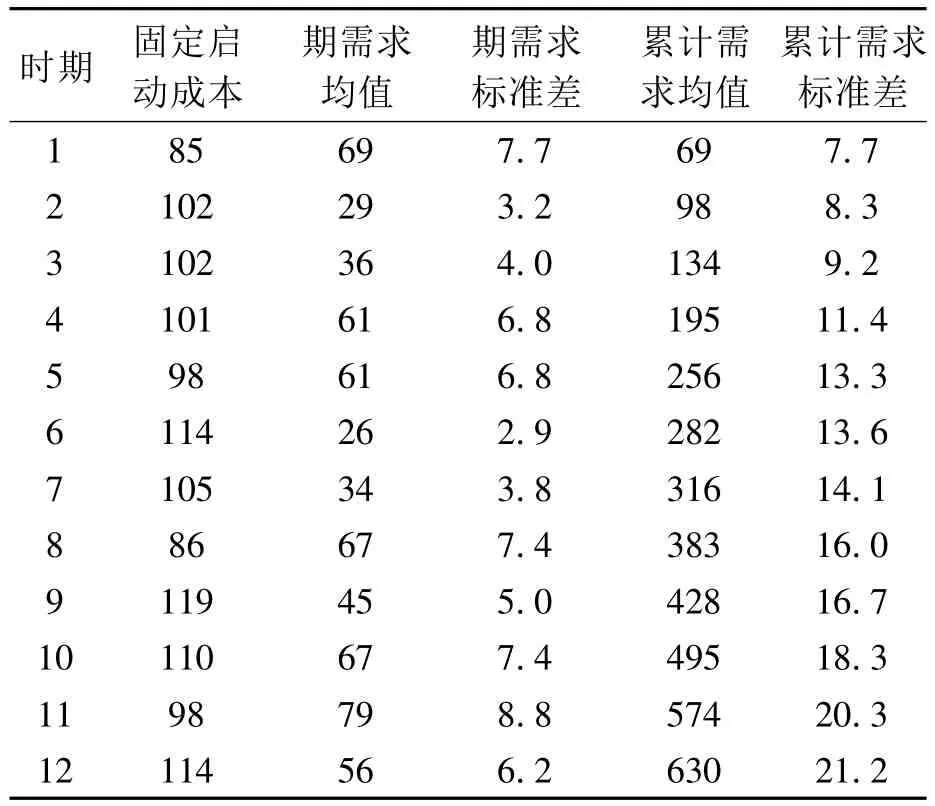
表1 算例1需求相关数据表

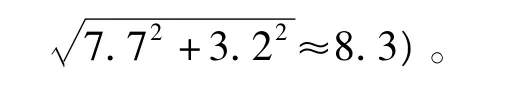
如 i=1，j=2 时，R'1(λQ，81)=0.9，通过调用软件Matlab 7.9.0.529(R2009b)中的gammaincinv函数，且 λ =81/69，故 Q≈79。

(1)设定 Qi，j的 上、下界值。该算例中，对于任何 1≤i＜ j≤T+1，下界值均可设为，上界值均可设为，这样可以涵盖表1中的累计需求均值的数据范围。

(2) 令 Qi，j==0。

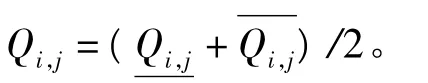
(6)输出 Qi，j，结束。

通过Matlab 7.9.0.529(R2009b)编程实现上述算法并成功运行，可得到相应 Qi，j(1≤i＜j≤T+1，j≥i+1)值，并对其进行四舍五入取整，得到累计批量 Qi，j数据，如表 2 所示。其中:Q2，6=262，表示从i=2期至 j=6期的累积批量值Q2，6为262单位;以下相关表格含义相同。

为验证该算法的正确性和可靠性，将该二分搜索算法运用于正态分布需求情形，根据表1相关数据(即文献［8］中“Table A1”的数据)，通过运行该算法的程序进行计算，亦可获得正态分布下累计批量数值，如表3所示。

用二分搜索算法得到的表3数据与文献［8］中的表格“Table A2”中的数据基本一致(表格中78个非零数据中75个完全相同。有3个数据不同:370与369、375与374、404与403，但都只相差1个单位值，其差异性几乎不存在)，从而可见二分搜索算法是正确而可靠的，并可用该算法和误差标准来进行后续的计算。

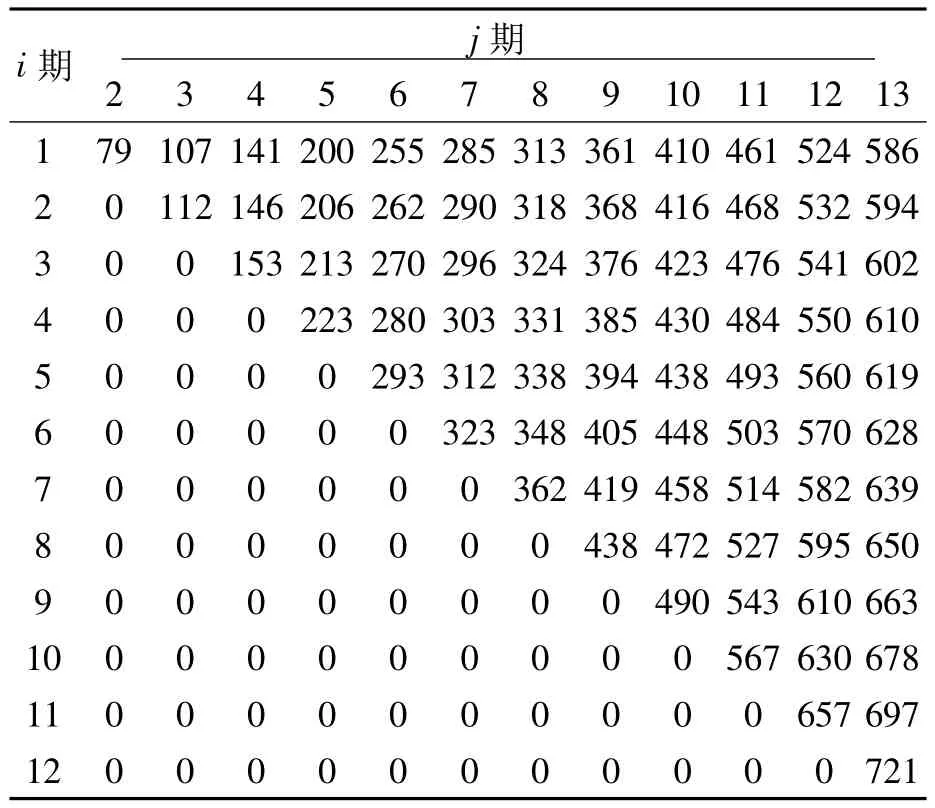
表2 算例1的爱尔朗分布下最优累积批量Qi，j数值表

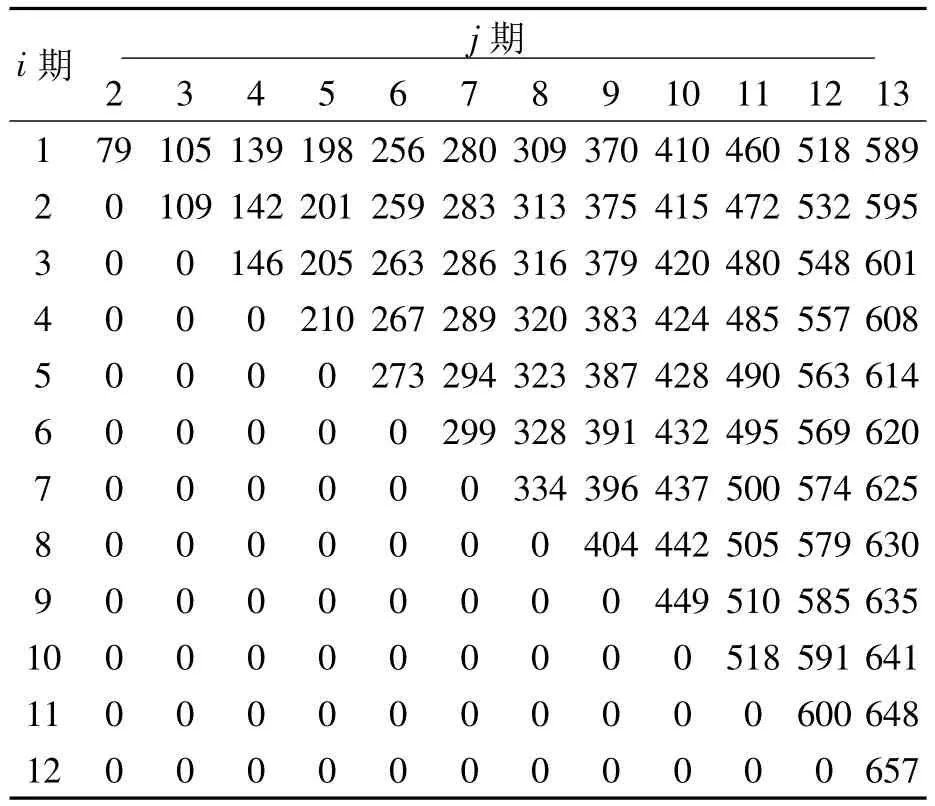
表3 算例1的正态分布下最优累积批量Qi，j数值表

表2与表3的数据相比，总体差别不大，但值得注意的是，随着两个表中“i期/j期”栏中的期数增大，相应的累计批量值在表2和表3之间的差异逐渐增大。通常是表2中的数据值大于表3中相对应的数据值，其体现的具体差异可用表2的非零数据元素除以表3中相应的非零数据元素表示，所获得的相应比值如表4所示。

对表4中的非零元素求平均及标准差，可得均值为1.03，标准差为0.03。由于标准差均值比为0.03/1.03≈0.03，故可认为均值1.03的置信度高，由此可知，表2中的元素值比表3中的元素值平均要大3%左右。

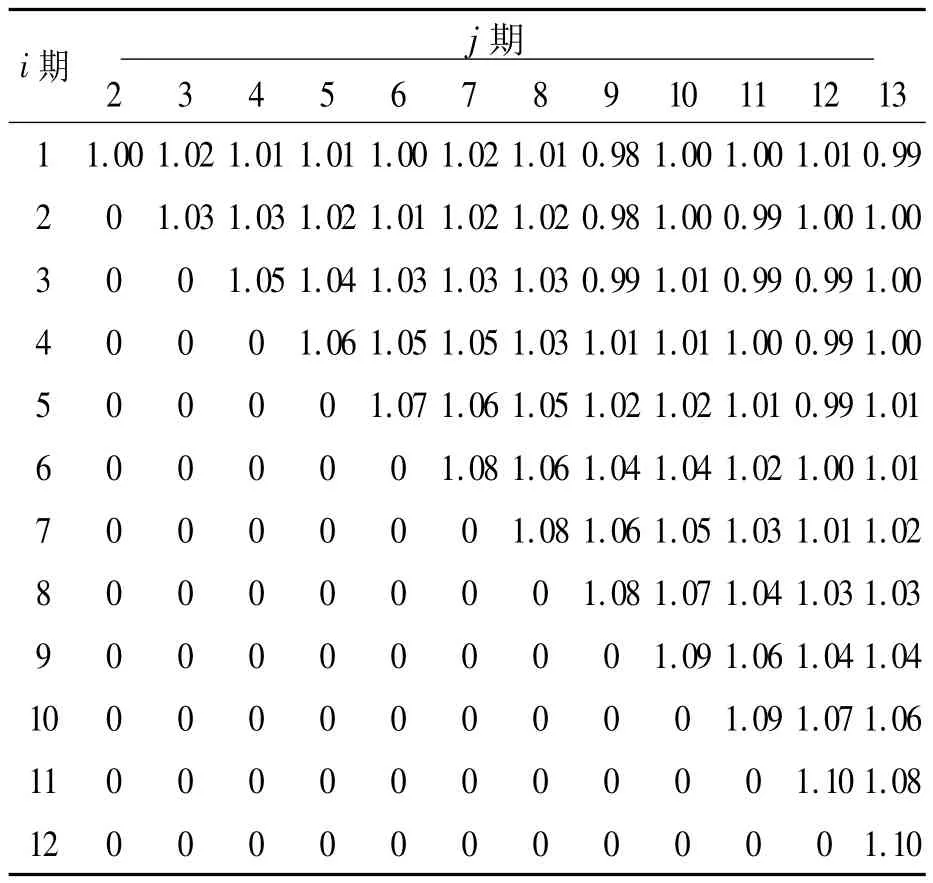
表4 算例1的最优累积批量比值表

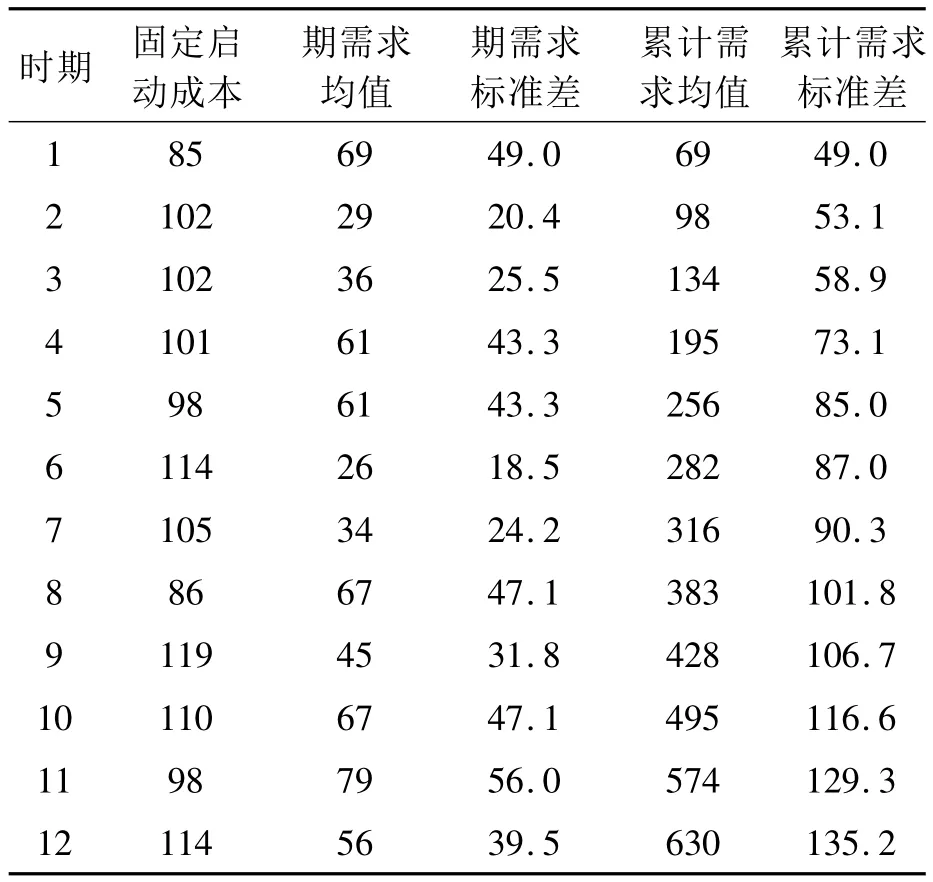
表5 算例2需求相关数据表

沿用算例1的有关方法，可获得算例2数据对应的爱尔朗分布、正态分布下的各最优累积批量数据以及两者各阶段最优累积批量的比值，如表6～表8所示。

显然表6中的元素数值均大于表7中相对应的元素数值。对表8中的非零元素求平均和标准差，可得均值为1.31，标准差为0.11。由于变异系数较小(0.11/1.31≈0.08)，可认为均值1.31的置信度较高，由此可认为，表6中的元素值比表3中相应的元素值平均大31%左右。

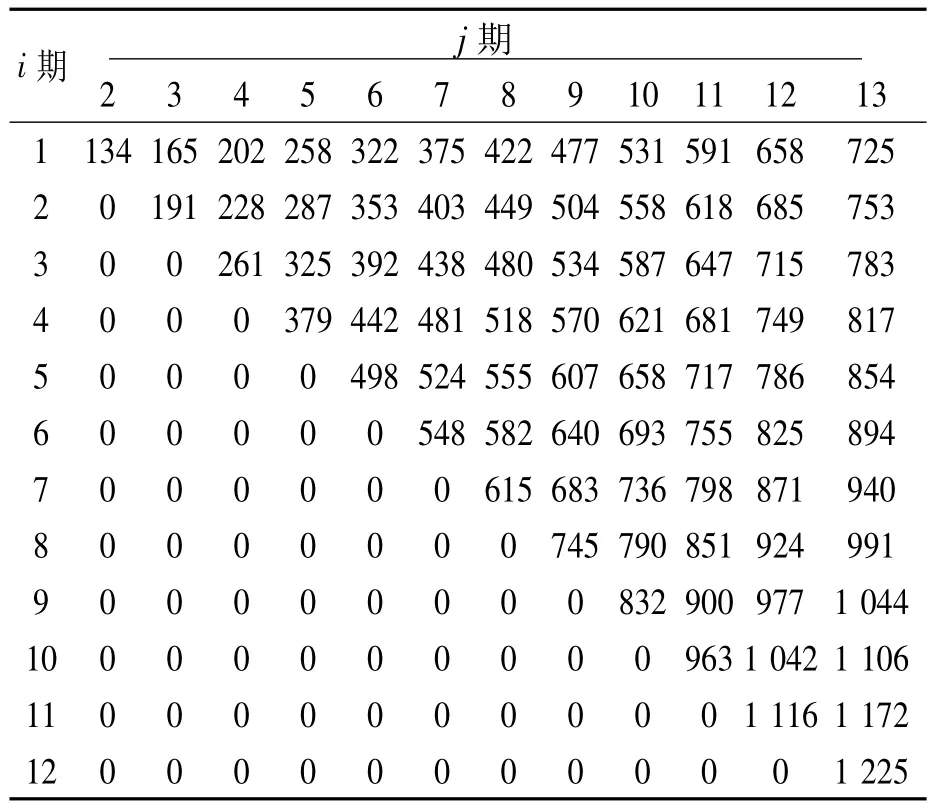
表6 算例2的爱尔朗分布下最优累积批量Qi，j数值表

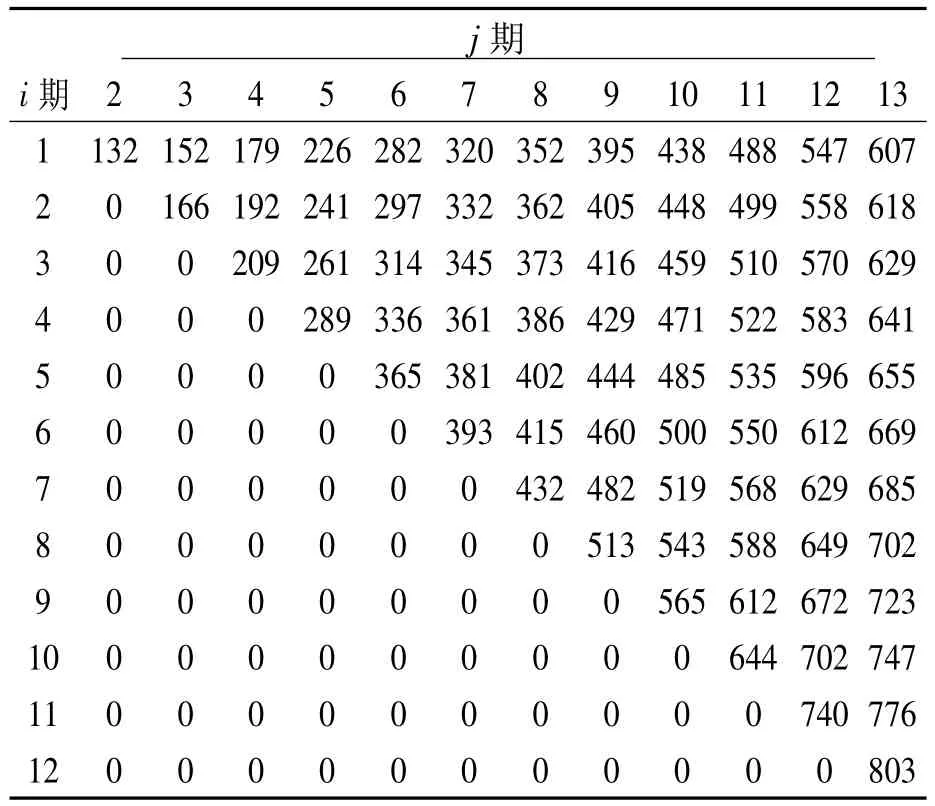
表7 算例2的正态分布下最优累积批量Qi，j数值表

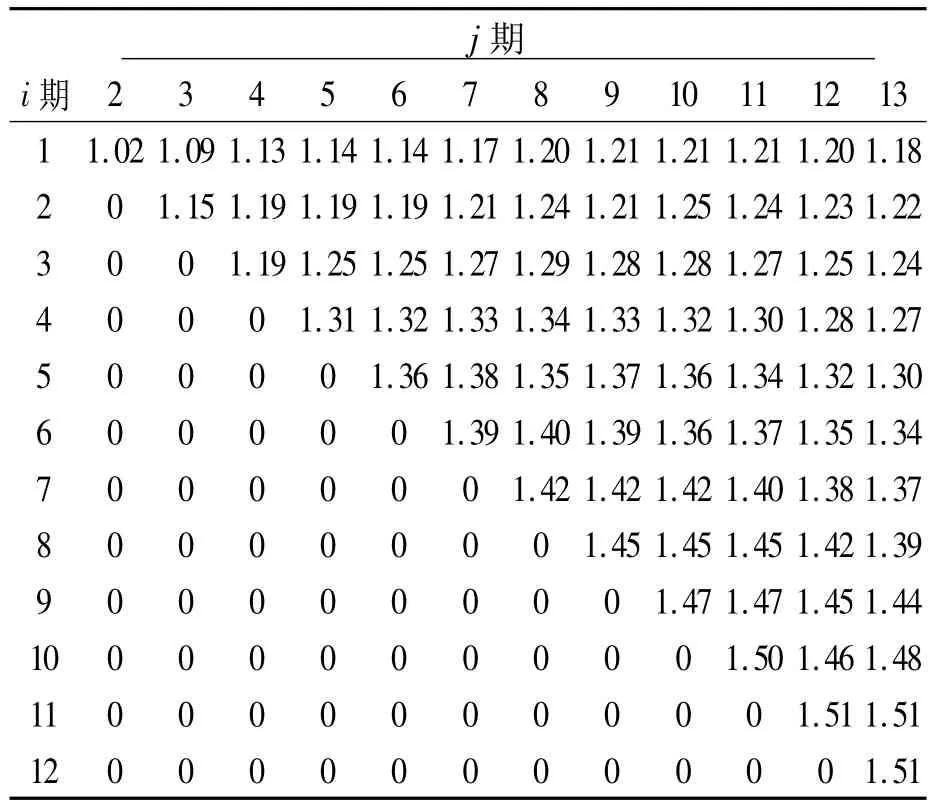
表8 算例2的最优累积批量比值表

3 比较分析

由上述数值试验的结果可知，随着标准差增大，爱尔朗分布下的各最优累积批量值也在增大。相对于标准差大幅度的变化，各最优累积批量值在爱尔朗分布需求下与在正态分布需求下，相互之间差异的变化并不很大。参照式(5)和式(6)，一方面，可能是由于在爱尔朗分布下当n较大时，其概率密度值gt(x)与相应的正态分布概率密度值 φt(x)差别不大，从而 Rt(Q，n)或 R't(λQ，n)的值与正态分布下相对应的值差异也不大;另一方面，式(5)或式(6)表达式形式与正态分布下的相应表达式形式类似(见文献［8］的相应表达式)，除了Rt(Q，n)或R't(λQ，n)与正态分布下的有所不同。并且，这种差异均会由式(5)或式(6)中的单位库存持有成本与单位缺货惩罚成本所形成的加权平均组合所弱化，从而会进一步平滑最优累积批量值在爱尔朗分布与正态分布之间的差异。

就最优总成本而言，对照式(4)与文献［8］中的式(7)，在给定的成本结构情况下(缺货回补成本与库存持有成本的比值β给定，生产及补货启动成本给定)，结合上述数值试验分析所得的结论，可知影响最优总成本大小的基础因素为相应的各最优累积批量值。当爱尔朗分布中的n充分大时，其累积概率值与相应正态分布累积概率值差异也较小。可见，爱尔朗分布需求下的各最优累积批量与正态分布下的相应最优累积批量相差不大，从而两者的最优总成本的差异性也不会很大。

如果考虑不允许或限制负需求的情形(即认为负需求是对需求刻画的高度失真)，就要加入惩罚因子。在类似算例2的情况中，变异系数相对较大时，用累积正态分布函数(Φ(x))描述需求而出现负需求的概率将会变得显著(负需求的概率为1-Φ(μ/σ))。例如在算例2的情形下，出现负需求的概率为0.08(1-Φ()≈0.08)，若惩罚因子足够大，则必存在使正态分布下各累积最优批量值的平均增幅充分大于31%的情况，使得应用爱尔朗分布所获得的相应最优总成本值比正态分布下的最优总成本值小，从而可能获得更好的动态批量策略。

4 结论

爱尔朗分布下的USILSP有助于在相关计算中避免负需求的误差影响，也有助于其相应的动态批量决策应用到产品需求更广泛的范围中，并且亦能为正态分布下USILSP相应最优累积批量值的计算提供对照和验证。此外，将二分搜索算法拓展于随机动态批量的情形中并编程，实现了相关计算。当然，若考虑到标准差及变异系数再进一步大幅增加的情况，即变异系数为1或非显著大于1，则爱尔朗分布就变成指数分布。用爱尔朗分布来描述相对低频随机需求的效果相对于正态分布而言，效果要更好些(正态分布函数通常适合用来描述高频随机需求)，从而相关最优累积批量值及动态批量策略的总成本值也可能更好些。如果变异系数显著大于1，则物品的相应需求可能为低频、间歇性需求，块状需求甚至慢速移动需求等，爱尔朗分布也不再适用，这时可考虑应用Gamma分布来描述该类物品的需求。其相应的动态批量模型、最优累积批量及优化策略是今后值得注意的研究内容。

［1］WAGNER H M，WHITIN T M.Dynamic version of the economic lot size model［J］.Management Science，1958，5(1):89-96.

［2］BRAHIMI N，DAUZERE-PERES S，NAJID N M，et al.Single item lot sizing problems［J］.European Journal of Operational Research，2006(1):1-16.

［3］WHYBARK D，WILLIAMS J.Material requirements planning under uncertainty［J］.Decision Sciences，1976，7(4):595-606.

［4］SILVER E.Inventory control under a probabilistic timevarying，demand pattern［J］.AIIE Transactions，1978，10(4):371-379.

［5］SOX C，MUCKSTADT J.Optimization-based planning for the stochastic lot scheduling problem［J］.AIIE Transactions，1997，29(5):349-357.

［6］TARIM S A，KINGSMAN B G.The stochastic dynamic production/inventory lot-sizing problem with service-level constraints［J］.International Journal of Production Economics，2004，88(1):105-119.

［7］WEMMERLOV U，WHYBARK D C.Lot sizing under uncertainty in a rolling schedule environment［J］.International Journal of Production Research，1984，22(3):467-484.

［8］VARGAS V.An optimal solution for the stochastic version of the Wagner-Whitin dynamic lot-size model［J］.European JournalofOperationalResearch，2009(2):447-451.

［9］NENES G，PANAGIOTIDOU S，TAGARAS G.Inventory management of multiple items with irregular demand:a case study［J］.European Journal of Operational Research，2010(2):313-324.

［10］AXSATER S.Inventory control［M］.［S.l.］:Springer，2006:85-87.

［11］CHANG Y J，YAO M J.New heuristics for solving the economic lot scheduling problem with reworks［J］.Journal of Industrial and Management Optimization，2011，7(1):229-251.

［12］BENTLEY J.Writing correct programs［J］.Communications of the Acm，1983，26(12):1040-1045.